Ondas en una y dos dimensiones y sus fenómenos

4. Ondas periódicas

La clasificación de una onda como periódica refiere al tiempo entre las perturbaciones, es decir,  una onda se llama periódica si el tiempo entre las perturbaciones es constante.

Estudiaremos el caso particular de las ondas periódicas armónicas, que son aquellas en las que el agente generador de la onda describe un movimiento armónico simple (M.A.S.). En el siguiente video se explica, para el caso de una onda periódica armónica que se desplaza por una cuerda, en qué consiste ese movimiento.

(Música del video: MixedSignals. Autor: Airtone. En dig.ccmixter.org/film. Licencia: CC BY-NC 3.0.)

No confundir la velocidad de la onda con la velocidad de las "porciones de cuerda". Como pudiste observar en el video, la onda se desplaza hacia la derecha, mientras que las "porciones de cuerda" se mueven hacia arriba y hacia abajo. Esto nos permite clasificar también a esta onda como transversal.

Analicemos cómo es la velocidad en algunas de las "porciones de cuerda" cuando la onda va pasando por ellas. Las siguientes imágenes muestran los vectores velocidad en diferentes posiciones del movimiento de una porción de la cuerda, míralas y lee detenidamente las aclaraciones.

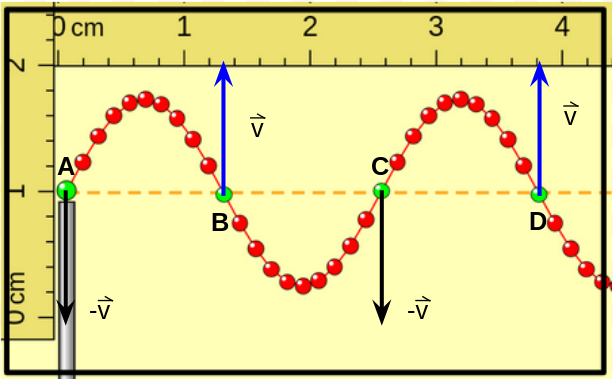
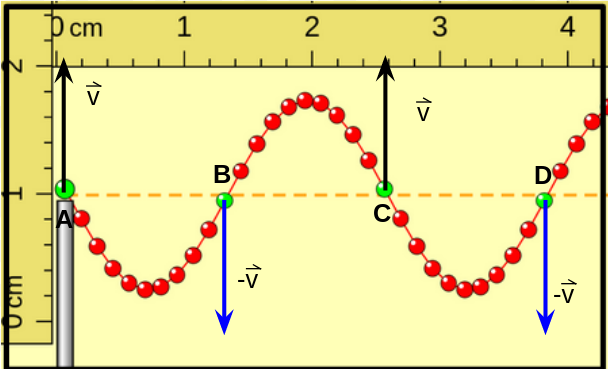
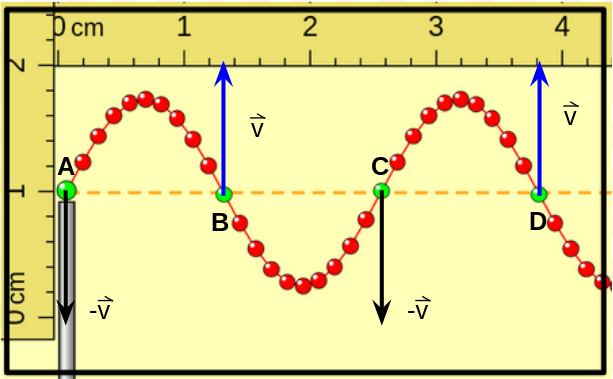
	En esta figura se representan las velocidades de las "porciones de cuerda" representadas con color verde cuando están pasando por la posición de equilibrio. Se marcaron con las letras A, B, C y D las cuatro porciones representadas con verde. Observar los círculos A y C tienen igual velocidad (igual módulo, dirección vertical y sentido hacia abajo) y que los puntos B y D también (igual módulo, dirección vertical y sentido hacia arriba).
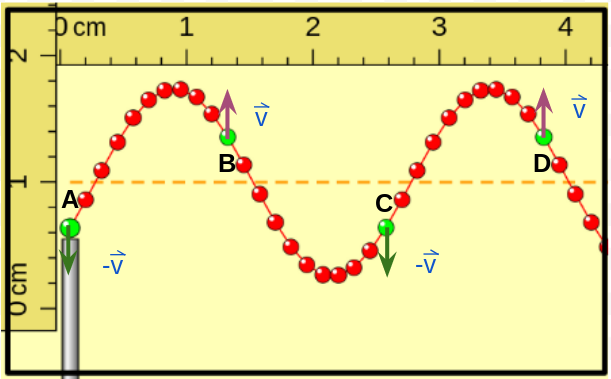
	En esta imagen las porciones A, B, C y D se desplazaron de la posición de equilibrio. Observar que las velocidades de A y C tienen menor módulo pero dirección y sentido son iguales que en la imagen anterior. Lo análogo sucede con los punto B y D.
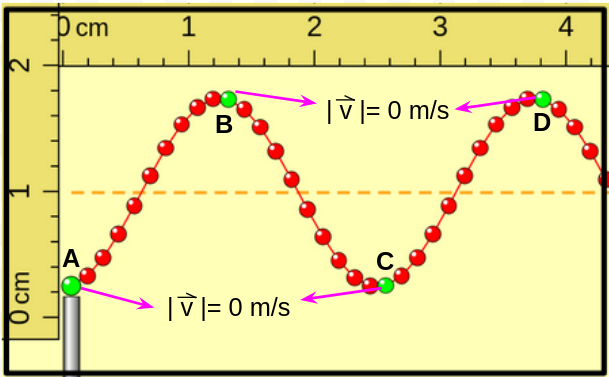
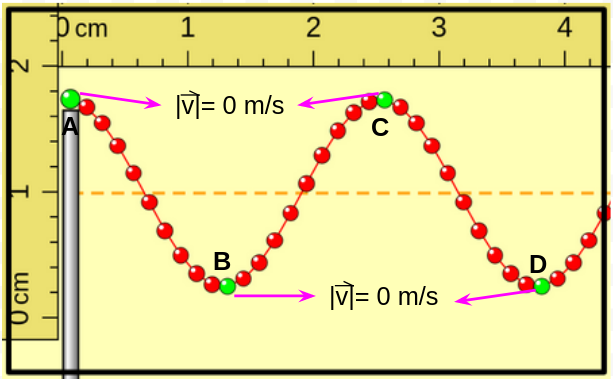
	Aquí las porciones A, B, C y D tienen la máxima separación de la posición de equilibrio, pero A y C se encuentran por debajo y B y D por encima. En este instante sus velocidades son nulas e inmediatamente después las porciones comienzan a moverse en sentido opuesto al que tenían antes de llegar a esta posición, como se muestra en la imagen a continuación.
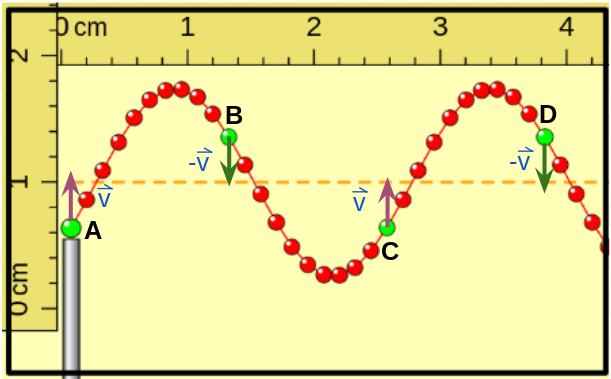
	La posición de las porciones indicadas ahora es por debajo de la posición de equilibrio, las velocidades de las porciones A y C son vertical hacia arriba y de igual valor y las de las porciones B y D son también de igual valor pero verticales hacia abajo.
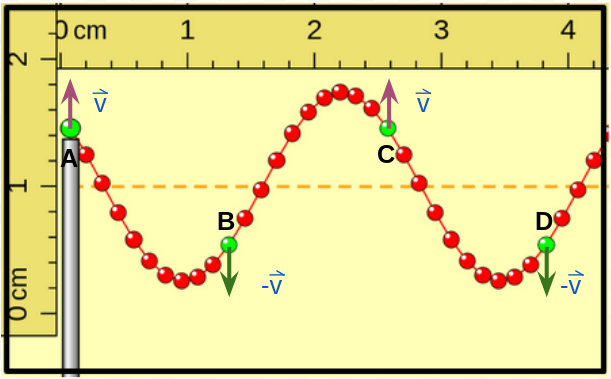
	En esta figura se representan las velocidades de las "porciones de cuerda" representadas con color verde cuando están nuevamente pasando por la posición de equilibrio. Las porciones A y C se mueven hacia arriba y las B y D hacia abajo.
	En esta imagen las porciones A, B, C y D se desplazaron de la posición de equilibrio, ahora A y C están por encima, pero B y D están por debajo. Observar que las velocidades de A y C tienen menor módulo pero dirección y sentido son iguales que en la imagen anterior. Lo análogo sucede con los punto B y D.
	Nuevamente las porciones A, B, C y D tienen la máxima separación de la posición de equilibrio, pero A y C se encuentran por encima y B y D por debajo. En este instante sus velocidades son nulas e inmediatamente después las porciones comienzan a moverse en sentido opuesto al que tenían antes de llegar a esta posición, como se muestra en la imagen a continuación.
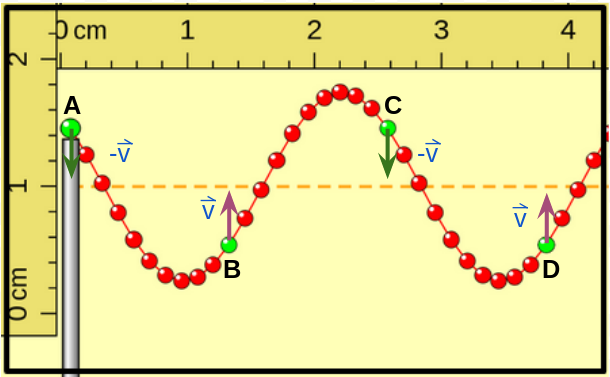	La posición de las porciones indicadas con A y C ahora es por encima de la posición de equilibrio, mientras que las indicadas con B y D por debajo, las velocidades de las porciones A y C son vertical hacia abajo y de igual valor y las de las porciones B y D son también de igual valor pero verticales hacia arriba. Un instante posterior se vuelve a obtener una imagen como la primera donde las porciones A, B, C y D alcanzan la posición de equilibrio con su velocidad máxima pero A y C se mueven hacia abajo y B y D se mueven hacia arriba, como se muestra a continuación, repitiéndose así todo el movimiento.
	Ídem a la imagen inicial.

La velocidad de las porciones de cuerda cambian con el tiempo, cuando una porción se encuentra en una cresta o en un valle su velocidad es cero, mientras que si se encuentra pasando por la posición de equilibrio de la cuerda su velocidad será máxima y su sentido será hacia arriba o hacia abajo.

Observación: el sentido de la velocidad de cada porción va a depender de cómo se encuentre ubicada la cuerda en el espacio, por ejemplo, si la cuerda se encuentra ubicada verticalmente, la dirección de la velocidad de cada porción de cuerda será horizontal y su sentido puede ser hacia la izquierda o hacia la derecha.

Las ondas periódicas pueden ser en uni, bi o tridimensionales.

Para simplificar su estudio, veremos sus características en una dimensión. Estas características también se aplican en dos y en tres dimensiones.