Equilibrio de rotación

2. Momento de una fuerza o torque

La figura muestra un cuerpo rígido que puede girar sobre un eje "O" perpendicular al plano de la figura. El cuerpo puede rotar alrededor de ese punto.

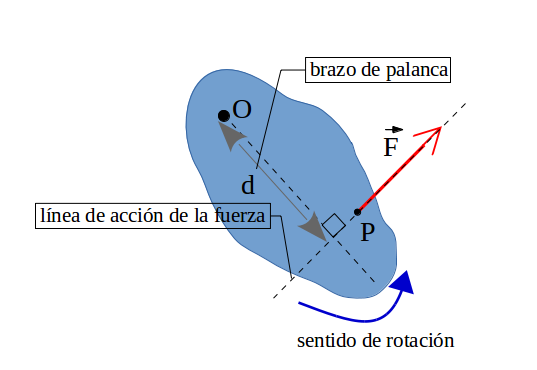
El brazo de palanca es una recta perpendicular a la línea de acción de la fuerza y que pasa por el eje de rotación O. La fuerza está aplicada en este caso en el punto P.

El momento de la fuerza que actúa sobre el cuerpo o torque, que se simboliza con la letra griega τ (tau), se define como el producto del módulo de la fuerza por el brazo de palanca, además debemos aclarar con respecto a qué punto se está determinando el torque, por eso el subíndice O en el símbolo τ_O:

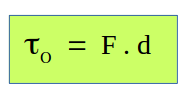
Las unidades del torque se deducen de la unidad de fuerza y de la unidad del brazo de palanca:

[F] = N (Newton)

[d] = m (metro)

[τ] = N.m

Al torque se le atribuye signo positivo o negativo, según el sentido de rotación que tiende a producir en el cuerpo: Si la fuerza tiende a hacer que el cuerpo gire en sentido horario (igual sentido que el del movimiento de las manecillas del reloj) su signo es negativo, y tiende a hacer girar al cuerpo en sentido antihorario (sentido contrario al movimiento de las manecillas del reloj) se le considerará con signo positivo.

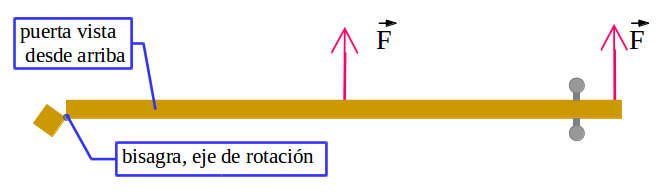
En la vida diaria el concepto de torque se utiliza con mucha frecuencia, por ejemplo, cuando se trata de abrir o cerrar una puerta. Si la fuerza se aplica en el extremo o en el punto medio de la puerta, los efectos en la rotación serán diferentes. Si la misma fuerza es aplicada en el extremo de la puerta el efecto en la rotación será mayor que si se la aplica en el punto medio de la puerta. Cuanto mayor sea la distancia del punto en que se aplica la fuerza al eje de rotación, mayor será el torque.

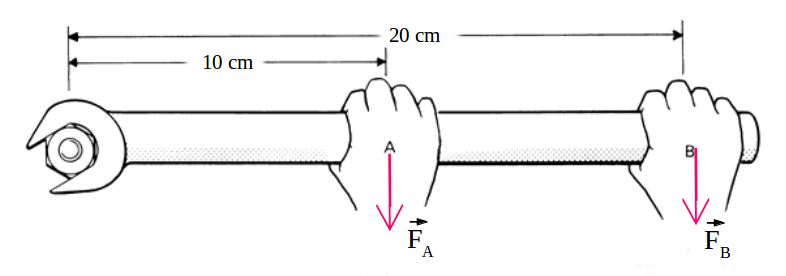
Otro ejemplo común es cuando se intenta apretar una tuerca, el efecto será mayor cuanto más lejos de eje de rotación, en este caso la tuerca, se aplique la fuerza.