¿Qué es la densidad?
5. Gráficas
5.3. Pendiente de una recta
Cuando dos magnitudes son directamente proporcionales al dividirlas podemos determinar la constante de proporcionalidad. También se puede determinar dicha constante a partir de la gráfica, calculando la pendiente de la recta.
- Determinación de la pendiente de una recta
Utilizaremos el mismo ejemplo que en los subcapítulos anteriores para la explicación.
1) Elegimos dos puntos cualesquiera que pertenezcan a la recta.
Al punto que tenga menor valor en el eje de las abscisas le llamaremos inicial (i) y al de mayor valor en el eje de las abscisas le llamaremos final (f).
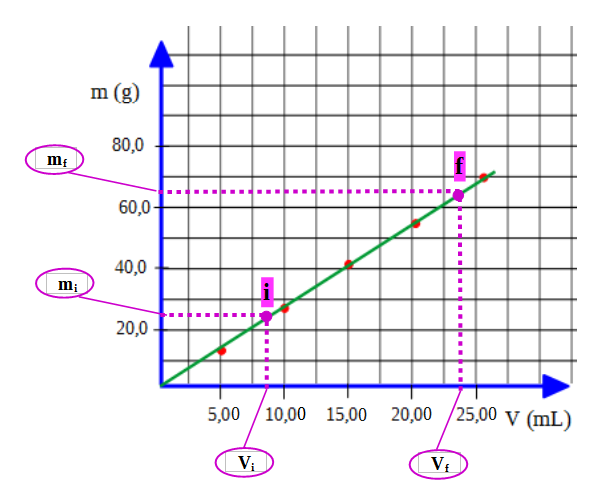
Las coordenadas del punto inicial son: Vi = 8,75 mL, mi = 25,0 g, y las del punto final son: Vf = 23,75 mL, mf = 65,0 g
2) Calculamos las variaciones de cada magnitud: ΔV y Δm. Recuerda que la letra griega delta (Δ) significa variación.
ΔV = Vf - Vi = 23,75 mL - 8,75 mL = 15,00 mL → ΔV = 15,00 mL
Δm = mf - mi = 65,0 g - 25,0 g = 40,0 g → Δm = 40,0 g
3) Cálculo de la pendiente:

En el caso de nuestro ejemplo:

El resultado es:

Podemos observar que la pendiente de la recta es igual a la constante de proporcionalidad que calculamos en el capítulo anterior dentro de un cierto margen de incertidumbre. Por tanto para este ejemplo particular la pendiente de la gráfica representa la densidad de los cuerpos usados para el experimento.
Recuerda que en toda medida siempre hay un margen de incertidumbre.