Trabajo mecánico
2. Trabajo realizado por una fuerza constante
2.2. Ejemplos
1) Sobre un cuerpo actúa una fuerza de módulo 20 N como se ve en la figura, el cuerpo se desplaza una distancia de 10 m.
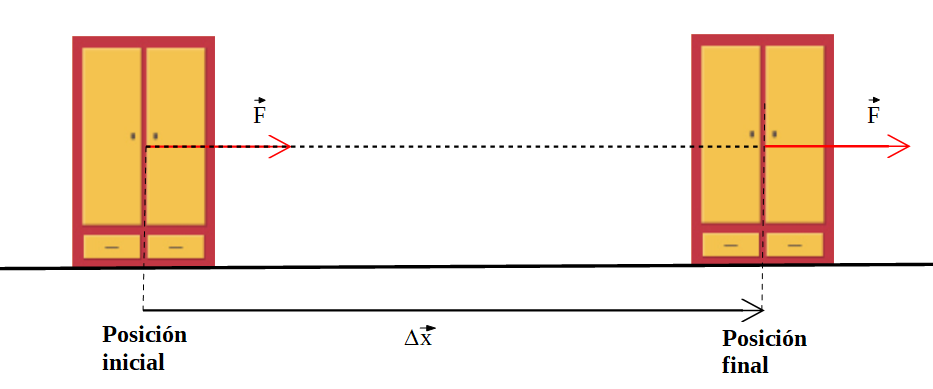
Nota: Se representa más abajo el vector desplazamiento, sólo para visualizarlo con más claridad.
Determinar el trabajo realizado por la fuerza ![]() entre la posición inicial y la final, indicadas.
entre la posición inicial y la final, indicadas.
Solución:
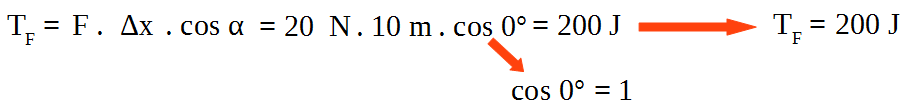
2) Sobre la caja de la figura está representada la fuerza normal a la superficie, su valor es de 30 N, el cuerpo se desplazó desde una posición inicial a la posición final, también está indicado el vector desplazamiento, su valor es de 2,0 m. Observar que el ángulo entre la fuerza normal y el vector desplazamiento es de 90°.
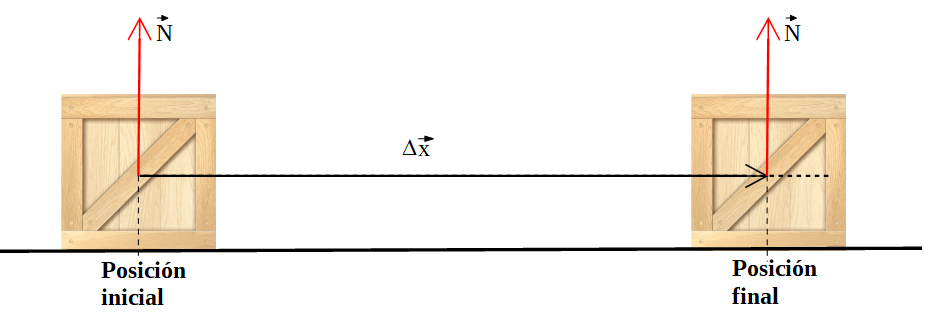
Determinar el trabajo realizado por la fuerza normal, entre la posición inicial y final indicadas.
Solución:
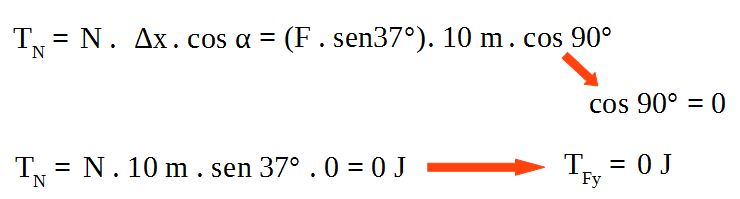
Conclusión: cualquier fuerza que tenga dirección perpendicular al desplazamiento, no realiza trabajo mecánico.
3) Sobre un baúl actúa una fuerza de módulo 20 N como se ve en la figura, el baúl se desplaza una distancia de 10 m.
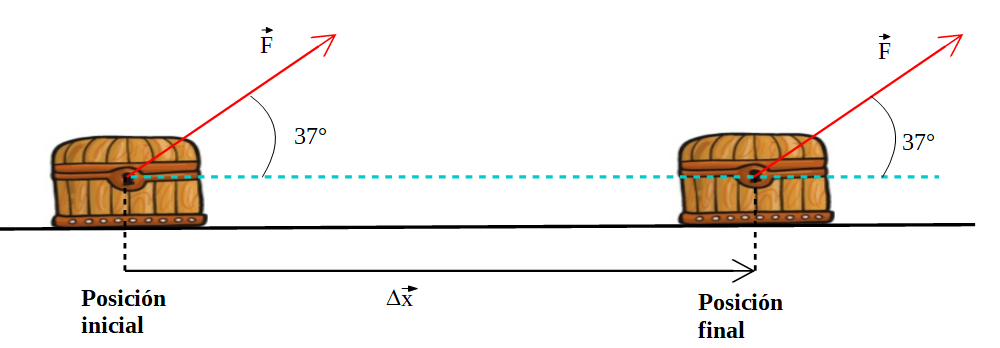
Determinar el trabajo realizado por la fuerza ![]() entre la posición inicial y final indicadas.
entre la posición inicial y final indicadas.
Solución:
![]()
En este último ejemplo se descompone la fuerza ![]() , para determinar el trabajo de cada una de las componentes de la fuerza y luego calcular el trabajo total sumándolos, TF = TFx + TFy:
, para determinar el trabajo de cada una de las componentes de la fuerza y luego calcular el trabajo total sumándolos, TF = TFx + TFy:
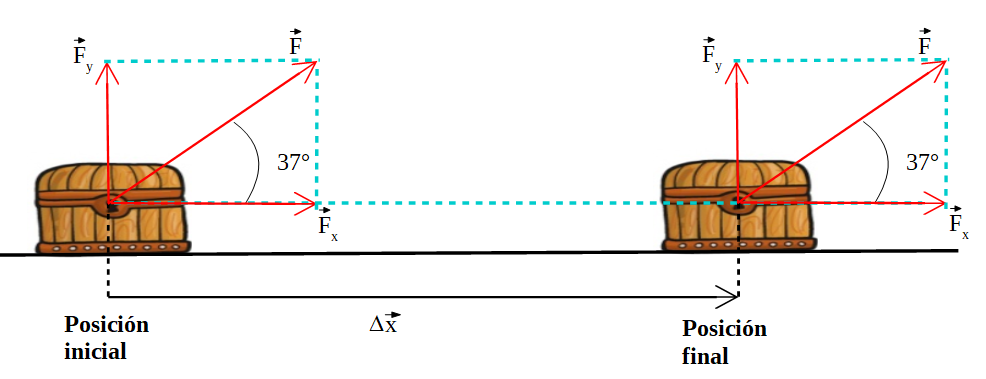
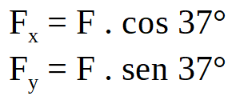
El trabajo total o trabajo neto realizado sobre un cuerpo, se determina sumando los trabajos de cada una de las fuerzas que actúan sobre el cuerpo. Por tanto al descomponer la fuerza ![]() tomamos el trabajo realizado por ella como la suma de los trabajos realizados por cada componente:
tomamos el trabajo realizado por ella como la suma de los trabajos realizados por cada componente:
![]()
El trabajo de la componente de ![]() en el eje x:
en el eje x:
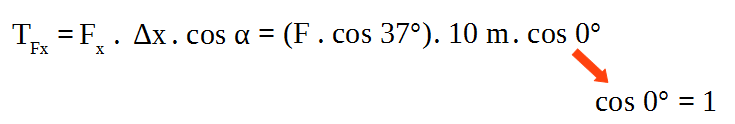
Al reordenar la expresión:

Se observa que esta expresión es igual a la usada para calcular el trabajo de ![]() , sin la descomposición de la fuerza:
, sin la descomposición de la fuerza:
![]()
El trabajo de la componende de ![]() en el eje y:
en el eje y:
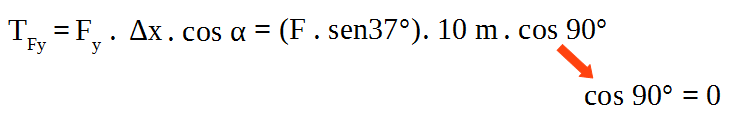
![]()
La suma de ambos trabajos:
![]()
La componente de la fuerza ![]() que realiza trabajo es solamente la que tiene igual dirección que el desplazamiento, en este caso es la componente x de
que realiza trabajo es solamente la que tiene igual dirección que el desplazamiento, en este caso es la componente x de ![]() . La componente que es perpendicular con respecto al desplazamiento no realiza trabajo, en este caso es la componente vertical, y.
. La componente que es perpendicular con respecto al desplazamiento no realiza trabajo, en este caso es la componente vertical, y.