Instrumentos y medidas
4. Cifras significativas
4.2. Cifras significativas y las operaciones matemáticas
Cuando se realizan operaciones con las medidas de un experimento, es importante respetar el número de cifras significativas del resultado. Las cifras significativas están relacionadas con la "precisión" de las medidas, por lo que no es posible que los resultados de las operaciones tengan mayor precisión que las medidas originales.
Suma y resta
Hemos comprado en un supermercado 1,0 kg de queso, luego en el almacén de la esquina compramos 540 g más. Para determinar la masa total de queso debemos sumar las masas.
El valor 1,00 kg que posee 3 cifras significativas y dos cifras después de la coma, de las que la última es la cifra insegura. Indicaremos la cifra insegura: ![]()
El valor 540 g, 3 cifras significativas, este valor tiene una unidad diferente del primer valor, por tanto lo convertiremos a kg, de ese modo los podremos sumar: 0,543 kg, el valor continúa teniendo 3 cifras significativas y tres cifras después de la coma, de las cuales la última el 3 es la cifra insegura: ![]()
Al realizar la suma:
![]()
Expresada de otra forma:
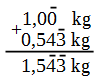
La suma tiene dos cifras seguras y dos inseguras, la expresión del resultado se debe realizar con todas las cifras seguras y la primera insegura, para ello debemos redondearlo, así que como el "3" es menor que cinco, el valor queda en 1,54 kg.
El resultado de sumar o restar dos medidas debe tener el mismo número de cifras decimales (lugares después de la coma) que el número que tenga menos.
Reglas de redondeo: en el siguiente enlace de Wikipedia puedes estudiar y ver ejemplos sobre el redondeo de las medidas.
Producto y división
Deseamos calcular el área de un piso para ir a comprar la cerámica: para hacer la medida usamos un metro y registramos 3,7 m de largo y 1,45 m de ancho.
Al calcular el área:
![]()
Los datos de las medidas, tienen dos y tres cifras significativas, el resultado del producto se debe expresar con igual cantidad de cifras significativas como el valor que tiene menor cantidad de cifras significativas, en este caso dos. Por tanto el resultado final será 5,4 m2. Tal como lo estudiaste en el enlace de Wikipedia, para redondear 5,365 a dos cifras, nos tenemos que quedar con el 5 y con el 3 pero como el número que le sigue al 3 es un 6 debemos sumar un dígito al 3, por lo que el resultado expresado con dos cifras queda 5,4 m2
El resultado de una multiplicación o división tendrá igual cantidad de cifras significativas como el factor que tenga menos cifras significativas.