CONCEPTOS CINEMÁTICOS

En este libro, se verán los conceptos cinemáticos, distancia, desplazamiento y realizaremos un sondeo de las ideas previas sobre velocidad y aceleración, tendrás también actividades y simulaciones.

Sitio:	Aulas \| Uruguay Educa
Curso:	Física - 3º C.B.
Libro:	CONCEPTOS CINEMÁTICOS
Imprimido por:	Invitado
Día:	domingo, 5 de mayo de 2024, 02:27

Tabla de contenidos

1. Sistema de referencia y vector posición
2. Trayectoria, distancia y desplazamiento
3. Rapidez y velocidad
4. Aceleración
5. Movimiento Rectilíneo Uniforme: MRU
6. Movimiento Rectilíneo Uniformemente Acelerado: MRUA
7. Representación gráfica de algunos movimientos rectilíneos
8. Repaso de la determinación de la pendiente de un gráfico
9. Créditos

1. Sistema de referencia y vector posición

Mira el siguiente video sobre sistema de referencia:

El vector posición es una magnitud vectorial que se mide en unidades de longitud y corresponde al lugar geométrico espacial que tiene el cuerpo en un instante dado.

En la figura se observa un auto que se movió en la recta horizontal, se ha tomado como sistema de referencia el eje x en el que se ha fijado su origen, se indica el vector posición inicial para el auto y el vector posición final.

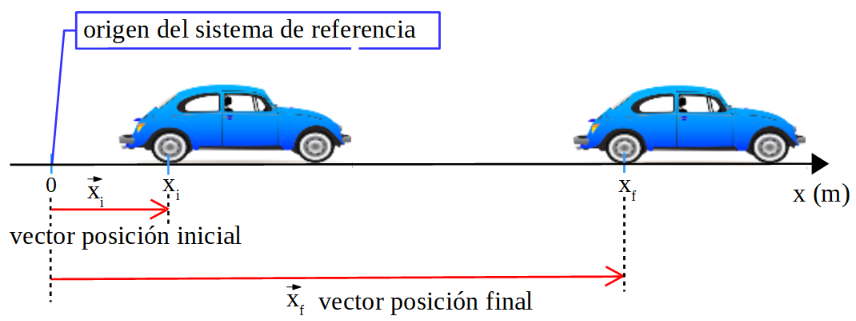
Sobre una línea recta se coloca un auto en dos posiciones diferentes y se indican los vectores posición inicial y final, con respecto al origen del sistema de referencia.

Cabe destacar que el vector posición inicial y final cambian si se modifica el origen del sistema de referencia (si cambia el observador).

También se puede elegir un sistema de referencia usando los ejes cartesianos en dos y tres dimensiones, dependiendo del movimiento que describa el sistema en estudio. Allí se necesitan más coordenadas para ubicar la posición inicial y final del sistema, y por tanto, los vectores posición, en el caso de dos dimensiones las coordenadas serán (x, y), en el caso de tres dimensiones serán (x, y, z).

La figura de abajo muestra el cambio de posición de una pelota. Se ha tomado para ubicar la posición inicial (x_i, y_i) y final (x_f, y_f) un sistema de referencia usando los ejes cartesianos (x,y). Están representados los vectores posición inicial () y final () de la pelota. Estos vectores tienen su origen en el origen del sistema de referencia y su extremo en la posición inicial y final respectivamente.

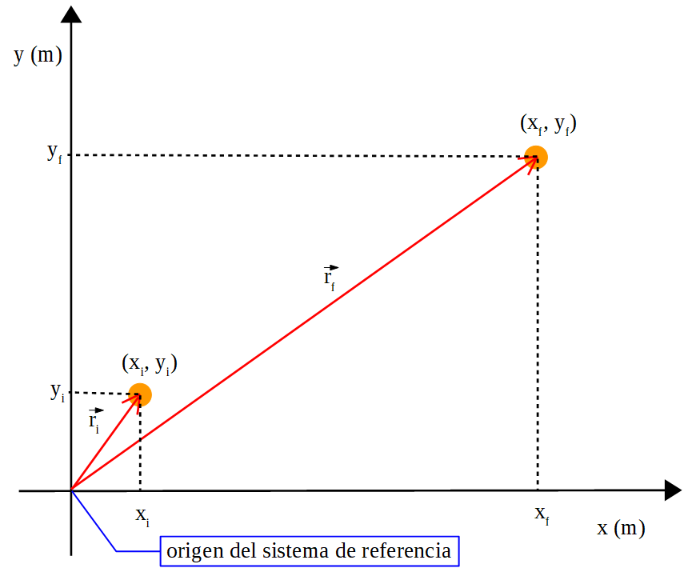
vectores posición inicial y final de una pelota en un gráfico xy

Análogamente si se agrega la tercera dimensión, se agrega otra coordenada, no se planteará porque excede los objetivos de este curso.

2. Trayectoria, distancia y desplazamiento

Mira el siguiente video:

Para las posiciones de los objetos del capítulo anterior, luego de definir los vectores posición inicial y final, podemos indicar en la imagen el vector desplazamiento. Para el caso del auto azul:

Sobre una línea recta se coloca un auto en dos posiciones diferentes y se indican los vectores posición inicial y final, con respecto al origen del sistema de referencia. Se indica además el vector desplazamiento, que tiene su origen la posición inicial y su extremo en la posición final del auto.

Para el caso de la pelota que se movía en el plano, el vector desplazamiento se representa así:

Se indica el vector desplazamiento en el plano

Realiza la siguiente tarea:

1) Escribe en tu cuaderno lo que has entendido por trayectoria, por distancia y por desplazamiento.

2) Indica si son magnitudes escalares o vectoriales.

3) En qué unidad se mide cada una de ellas.

Si es necesario, vuelve a mirar el video.

Prueba ahora con un simulador, ingresa en el siguiente enlace, allí verás la siguiente imagen: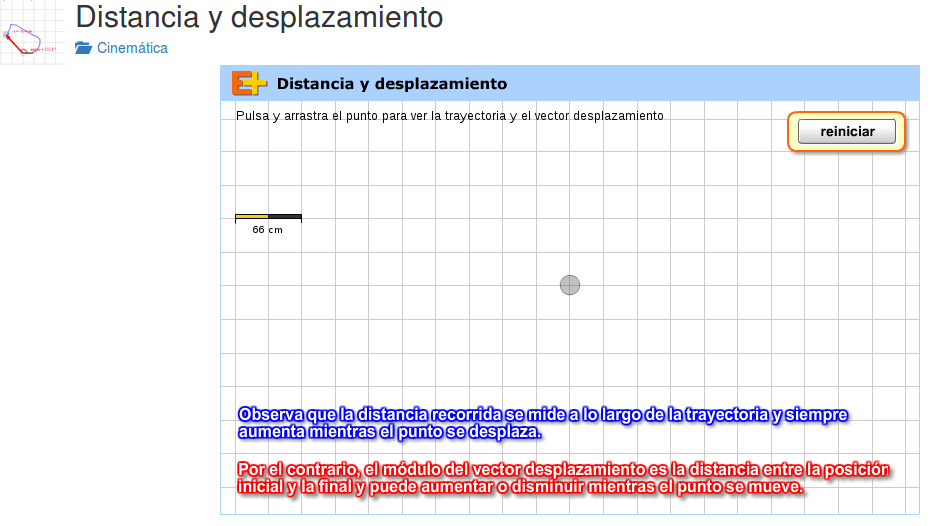

Sigue las instrucciones que allí aparecen, de ese modo podrás comprender con claridad la diferencia entre distancia y desplazamiento.

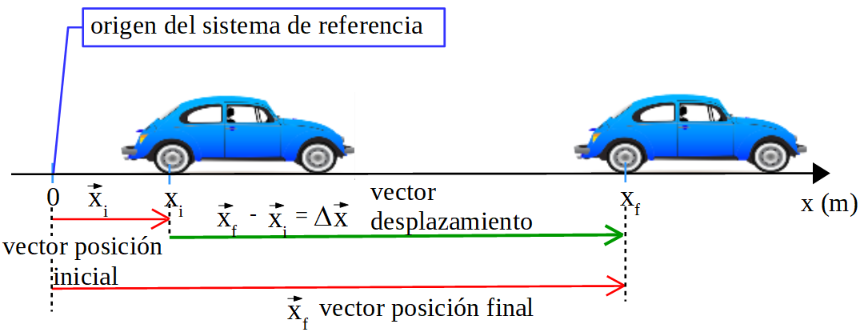
Desplazamiento:

Si el desplazamiento es en línea recta horizontal, usamos la coordenada x para definir los vectores posición inicial y final, con respecto al origen del Sistema de Referencia: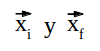

El desplazamiento se determina de la siguiente forma:

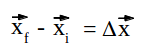
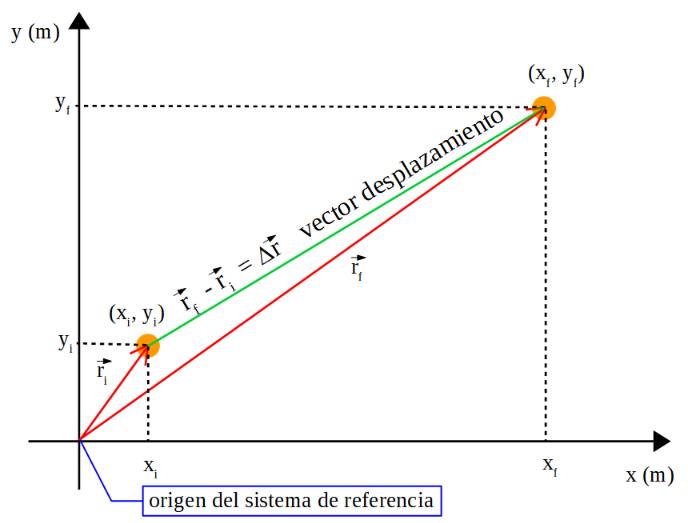
Si el desplazamiento es en línea recta pero vertical, se utiliza el eje y de coordenadas y se definen los vectores posición inicial y final:

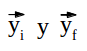
y el desplazamiento es:

3. Rapidez y velocidad

Rapidez y velocidad son dos magnitudes cinemáticas que suelen confundirse con frecuencia.

Recordar que la distancia recorrida y el desplazamiento realizado por un cuerpo son dos magnitudes diferentes.

Rapidez instantánea: es la rapidez que tiene un cuerpo en un instante cualquiera.

Rapidez media: es la distancia recorrida por un cuerpo dividido por el intervalo de tiempo.

Si la rapidez instantánea es constante en un intervalo de tiempo, su valor será igual al de la rapidez media en ese intervalo.

La rapidez es una magnitud escalar, por lo tanto no tiene en cuenta la dirección ni el sentido del movimiento.

El velocímetro de un vehículo (automóvil, moto, camión, etc.) informa la rapidez instantánea del mismo, no indica la dirección y el sentido del movimiento.

Concepto de rapidez media, magnitud escalar que relaciona la distancia con el tiempo

ecuación de rapidez. rapidez, v es igual a distancia recorrida dividido el tiempo.

La velocidad es una magnitud vectorial.

La velocidad instantánea: es la velocidad que tiene un cuerpo en un instante cualquiera con su módulo, dirección y sentido. Se puede determinar como el desplazamiento del cuerpo (magnitud vectorial) dividido un intervalo de tiempo muy muy pequeño.

La velocidad media: es el desplazamiento de un cuerpo dividido un intervalo de tiempo. Si el cuerpo se mueve en una trayectoria rectilínea, no cambia su sentido de movimiento y el módulo de su velocidad instantánea es constante, ésta será igual a la velocidad media.

Concepto de velocidad media, magnitud vectorial que relaciona el desplazamiento con el tiempo.

ecuación de velocidad. Vector velocidad igual al vector desplazamiento dividido el tiempo

La unidad de medida de la rapidez y de la velocidad en el Sistema Internacional de unidades es metros dividido segundos o m/s.

Mira el siguiente video:

4. Aceleración

Si un cuerpo experimenta un cambio en su velocidad en un intervalo de tiempo, está acelerado.

La aceleración es una magnitud vectorial. Se determina como el cambio de velocidad (en módulo, dirección y/o sentido) dividido el intervalo de tiempo en que se produce dicho cambio.

Si un cuerpo tiene una gran aceleración, significa que su velocidad cambia rápidamente. Si tiene una aceleración muy pequeña, su velocidad cambia lentamente y si su aceleración es cero su velocidad no cambia.

Que un cuerpo tenga una gran velocidad no significa que tenga una gran aceleración y viceversa. La aceleración informa cómo cambia la velocidad. Si un automóvil se está desplazando con velocidad constante (aceleración cero) y su dirección se modifica, significa que experimentó una aceleración que hace que su velocidad cambie. El volante de un vehículo hace que cambie la dirección y el sentido del movimiento, y por tanto produce que el vehículo acelere.

En este módulo solo se analizarán situaciones con cuerpos que modifican su velocidad de forma constante, es decir, que poseen aceleración constante. De esta forma, la aceleración instantánea y la media serán iguales y no se hará ninguna distinción entre ellas, se la llamará simplemente aceleración.

Concepto de aceleración, magnitud vectorial que relaciona el cambio de velocidad con el tiempo en que ocurre dicho cambio.

Ecuación para calcular la aceleración: variación de la velocidad dividido el intervalo de tiempo de dicha variación.

Siendo la variación de la velocidad una operación vectorial:

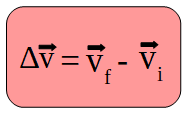
ecuación para determinar el vector variación de velocidad como: vector velocidad final menos vector velocidad inicial.

La unidad de medida de la aceleración en el S.I. es la unidad de velocidad dividido la unidad de tiempo, es decir, m/s/s eso resulta en: m/s².

Mira el siguiente video, en el mismo se tratan movimientos rectilíneos, así los vectores velocidad inicial y final son colineales y por lo tanto, se van a operar como vectores colineales. En este video no se coloca sobre las magnitudes la notación de los vectores, aunque lo correcto sería hacerlo.

5. Movimiento Rectilíneo Uniforme: MRU

El Movimiento Rectilíneo Uniforme: MRU es un movimiento que tiene una trayectoria rectilínea y su velocidad es constante, por lo tanto su aceleración es cero.

Realiza la siguiente actividad:

1) Ingresa en el siguiente simulador (puede ser que demore un poco en cargar), en él podrás estudiar cómo cambia la posición con respecto al tiempo de un hombre que se mueve en línea recta.

2) Selecciona primero la aceleración con valor cero para que describa un MRU.

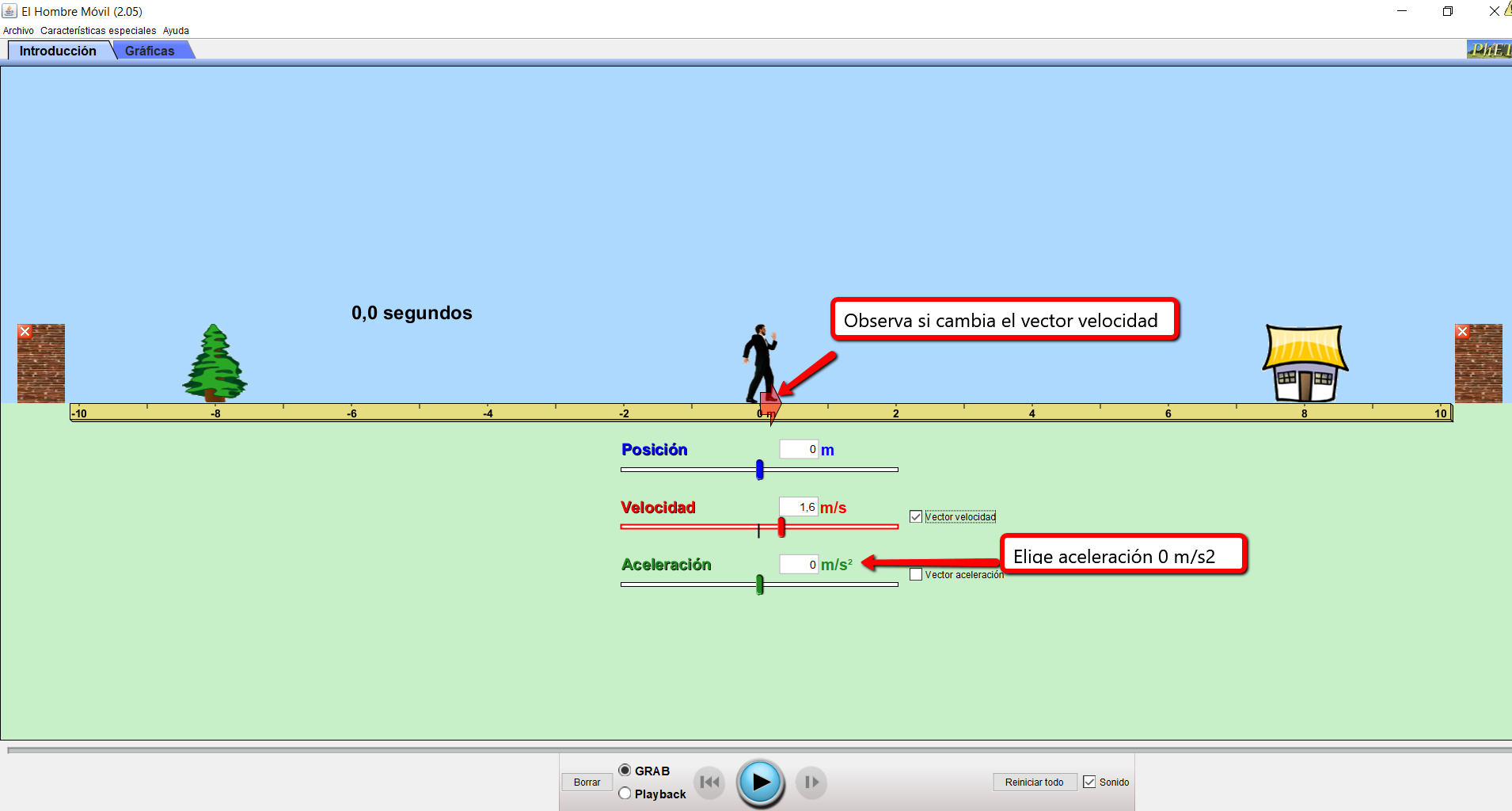
Captura de imagen del simulador

3) Elige primero una velocidad hacia la derecha y luego hacia la izquierda. Observa cómo varía la posición en cada caso. Para que el hombre comience a moverse debes apretar el botón play (botón circular celeste con una flecha hacia la derecha).

4) Luego pasa a la pestaña Gráficas y repite los pasos anteriores. Observa y registra la forma de las gráficas para cada caso.

5.1. Gráfica posición en función del tiempo de un MRU

Se analizará el caso de una persona que se mueve en línea recta con velocidad constante desde la posición -2 m hasta la posición 4 m. La imagen muestra las posiciones y los tiempos, suponiendo que tardó 3 segundos en moverse desde la posición inicial a la final.

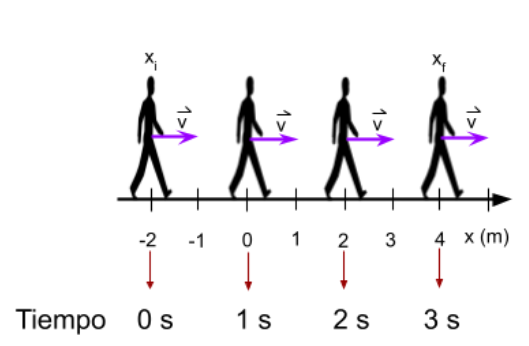
Persona moviéndose sobre una recta horizontal, desde la posición -2 metros hasta la posición 4 metros, se representó la posición de las personas en diferentes tiempos.

Al graficar la posición de la persona en función del tiempo, se obtiene la siguiente gráfica:

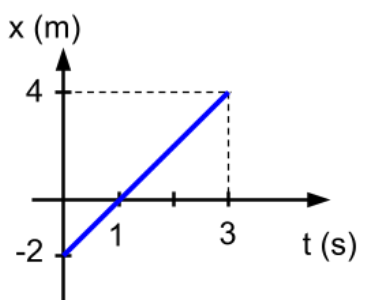
gráfica posición en función del tiempo

La pendiente de esta recta se puede calcular de la siguiente forma:

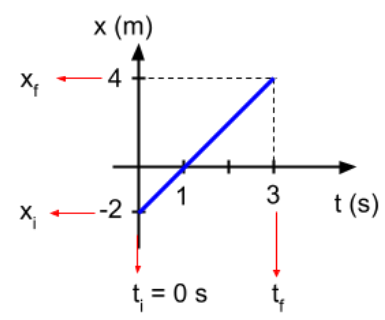
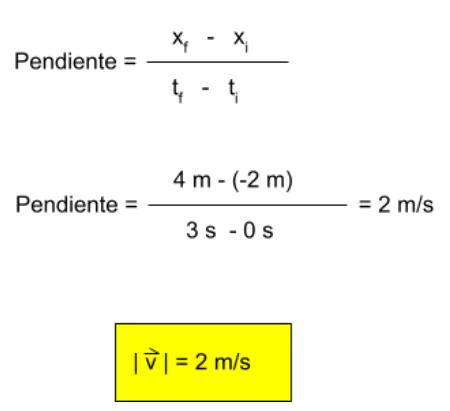
Gráfica posición en función del tiempo, se ha indicado las posiciones inicial y final así como los tiempos inicial y final determinación de la pendiente igual posición final menos la inicial dividido la diferencia entre los tiempos final e inicial. Pendiente igual (4 m- 2 m) / (3 s - 0 s) = 2 m/s. Módulo de la velocidad = 2 m/s

Se observa aquí que las unidades de la pendiente son unidades de velocidad, por tanto, el significado físico de la pendiente es el módulo de la velocidad que tiene la persona, en este caso es constante y su valor es 2 m/s.

5.2. Gráfica velocidad en función del tiempo en un MRU

Al analizar la velocidad en el movimiento anterior:

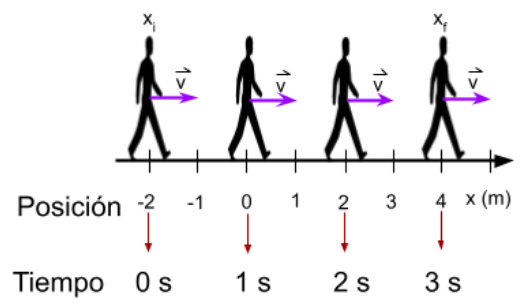
Persona moviéndose sobre una recta horizontal, desde la posición -2 metros hasta la posición 4 metros, se representó la posición de las personas en diferentes tiempos.

La gráfica del módulo de la velocidad en función del tiempo para este movimiento es una recta paralela al eje del tiempo porque la velocidad permanece constante en los 3 segundos considerados.

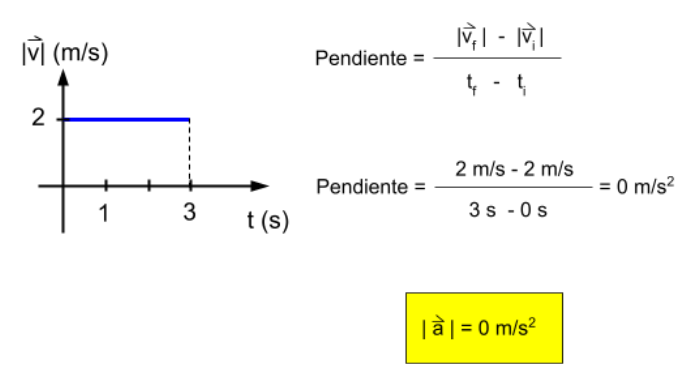
Gráfica módulo de la velocidad en función del tiempo.

También se puede calcular el área bajo esta gráfica.

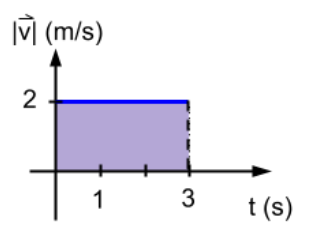
Gráfica módulo de la velocidad en función del tiempo. Se ha indicado con otro color el área bajo la recta. Área bajo el gráfico igual a área de un rectángulo igual a base por altura. Área bajo el gráfico igual tiempo por el módulo de la velocidad. Área bajo la gráfica igual 3 s por 2 m/s igual a 6 m.

El área bajo la curva corresponde al área de un rectángulo que se determina base por altura. La base es el tiempo, en este caso 3 segundos y la altura es el valor de la velocidad 2 m/s. Al analizar las unidades se observa que queda en metros (m). El significado físico de este cálculo es el módulo del desplazamiento de la persona. El desplazamiento es una magnitud vectorial, se determina como el vector posición final menos el vector posición inicial. A continuación se muestran los vectores posición inicial y final, y se determina el desplazamiento con todas sus características.

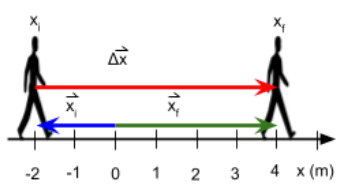
Persona ubicada en la posición inicial y final de su movimiento. Se han representado los vectores posición inicial, final y el vector desplazamiento.

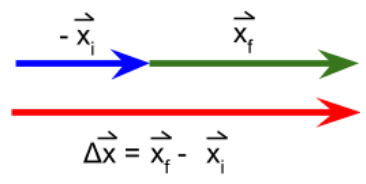
Representación de la operación vectorial: vector posición final menos vector posición final.

Observa que el módulo del vector desplazamiento es 6 m, esto coincide con el valor determinado con el área bajo la gráfica.

De esta forma el vector desplazamiento es 6 m, 0º o 6 m horizontal a la derecha.

Recuerda que 0º indica que el vector forma 0º con respecto al eje x.

5.3. Gráfica aceleración en función del tiempo para un MRU

En este caso se trata de un movimiento rectilíneo en el cual la velocidad es constante y por tanto la aceleración vale cero. La gráfica del módulo de la aceleración en función del tiempo es una recta sobre el eje del tiempo.

gráfica del módulo de la aceleración en función del tiempo.

6. Movimiento Rectilíneo Uniformemente Acelerado: MRUA

El Movimiento Rectilíneo Uniformemente Acelerado: MRUA es un movimiento que tiene una trayectoria rectilínea y su aceleración es constante, por lo tanto su velocidad se modifica de forma uniforme.

Realiza la siguiente actividad:

1) Utiliza el mismo simulador del capítulo anterior, ahora elige una aceleración hacia la derecha.

2) Observa cómo se va modificando el vector velocidad a medida que transcurre el tiempo.

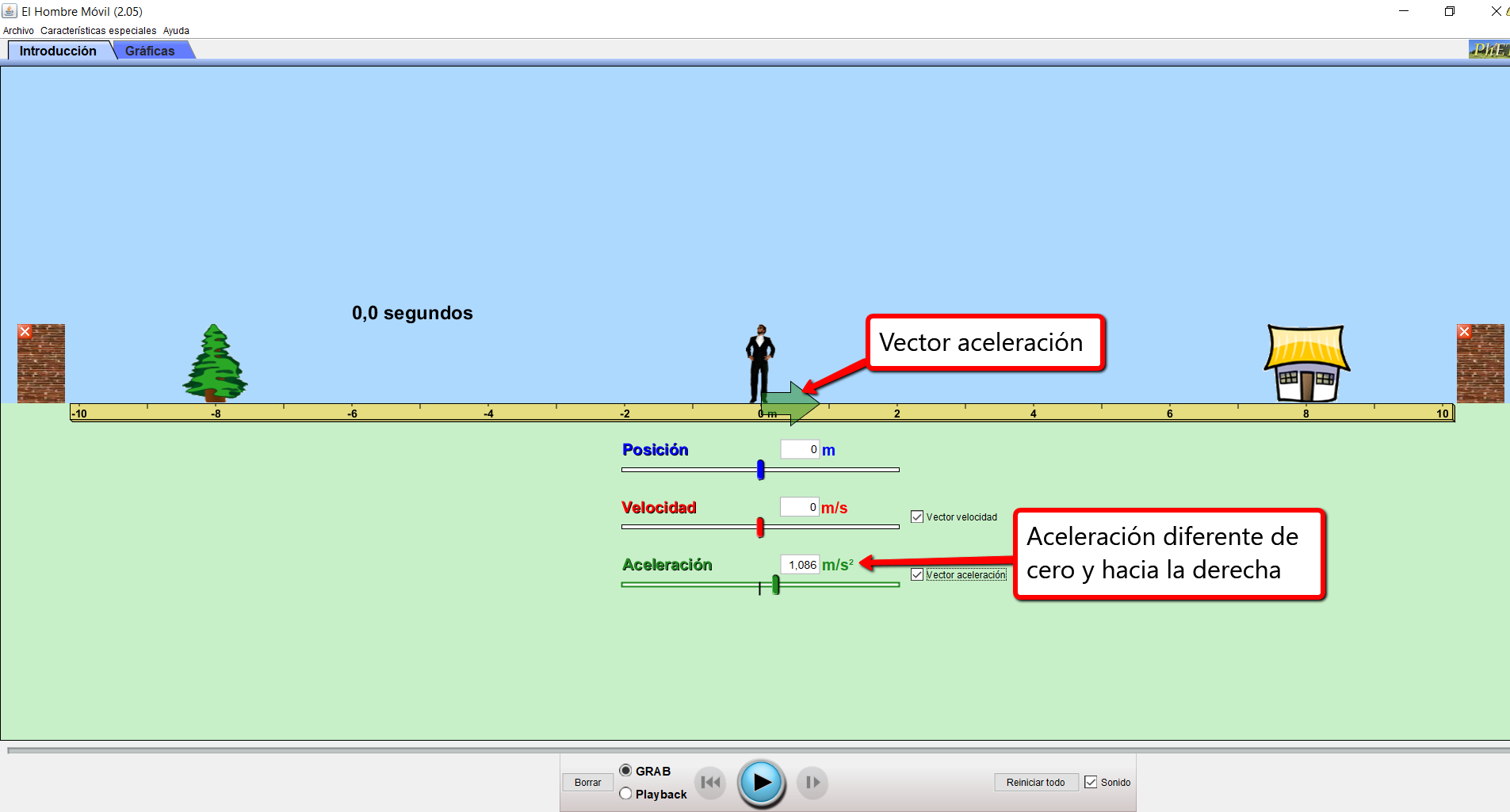
Captura de pantalla simulador phet el hombre móvil

3) Elige luego una aceleración hacia la izquierda. Observa cómo varía el vector velocidad en cada caso. Para que el hombre comience a moverse debes apretar el botón play (botón circular celeste con una flecha hacia la derecha).

4) Luego pasa a la pestaña Gráficas y repite los pasos anteriores. Observa y registra la forma de los gráficos para cada caso.

6.1. Gráfica velocidad en función del tiempo en un MRUA

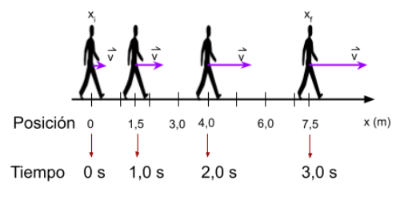
Se analiza ahora el caso de una persona que se mueve en línea recta desde la posición 0 m hasta la posición 7,5 m. La imagen muestra las posiciones y los tiempos, suponiendo que tardó 3 segundos en moverse desde la posición inicial a la final. Se puede observar que no tarda el mismo tiempo en recorrer la misma distancia, por tanto, su velocidad no es constante.

Persona moviéndose sobre una recta horizontal, desde la posición 0 metros hasta la posición 7,5 metros. Se representó el vector posición sobre la persona para los diferentes tiempos.

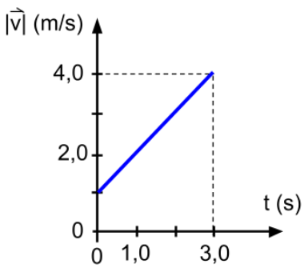
La gráfica de velocidad en función del tiempo para este movimiento es la que se muestra a continuación:

Gráfica módulo de la velocidad en función del tiempo.

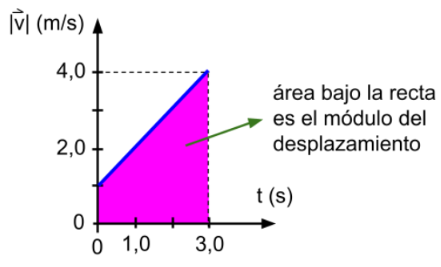
Del área bajo esta gráfica podemos determinar el módulo del desplazamiento de la persona:

Gráfica módulo de la velocidad en función del tiempo. Se muestra pintada el área bajo el gráfico y se indica que corresponde al módulo del desplazamiento.

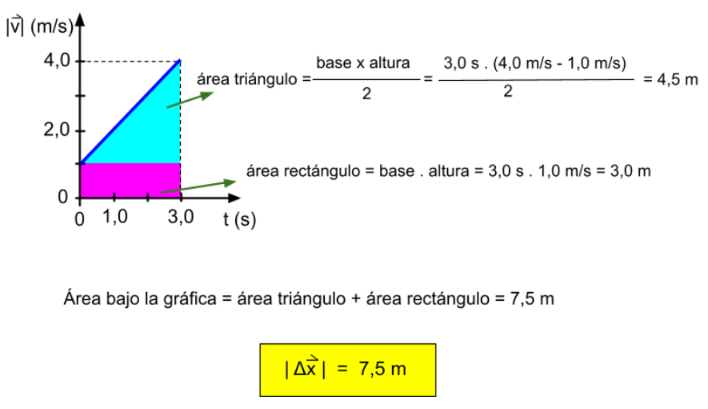
Para calcular el área bajo la gráfica, se puede hallar el área de un trapecio o dividir el área en un rectángulo y un triángulo:

Gráfica módulo de la velocidad en función del tiempo. Se muestra el cálculo del área bajo la recta, como la suma del área de un triángulo más la de un rectángulo.

A continuación se muestra la representación del vector desplazamiento para este ejemplo:

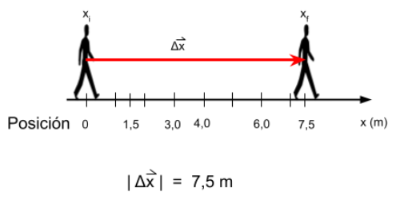
Representación de la posición inicial de la persona, se muestra el vector desplazamiento.

En este caso el vector desplazamiento de la persona es 7,5 m, 0º o 7,5 m horizontal a la derecha.

6.2. Gráfica posición en función del tiempo de un MRUA

Para la situación analizada,

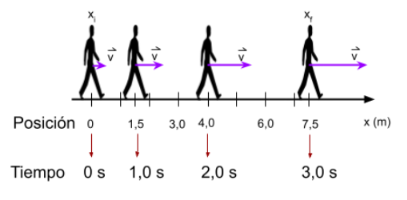
Persona moviéndose sobre una recta horizontal, desde la posición 0 metros hasta la posición 7,5 metros, se representó la posición de las personas en diferentes tiempos, así como también los vectores velocidad instantánea en dichos tiempos.

La gráfica de la posición de la persona en función del tiempo es:

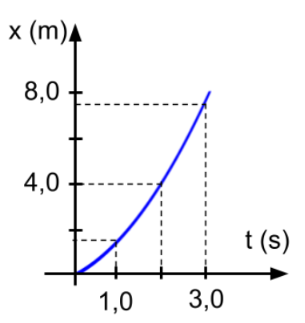
gráfica posición en función del tiempo. La forma es una rama de parábola

Se puede observar que la forma de la gráfica es una curva, en cursos más avanzados verás que se trata de una rama de parábola. En este caso la velocidad va aumentando, para poder determinar el módulo de la velocidad en cada instante, se debe trazar una tangente a la parábola en un determinado tiempo y la pendiente de dicha tangente es el módulo de la velocidad en ese instante.

6.3. Determinación de la aceleración del MRUA y su representación gráfica

Para determinar la aceleración, calcularemos la pendiente de la gráfica velocidad en función del tiempo:

Gráfica módulo de la velocidad en función del tiempo, se indican las velocidades inicial y final así como los tiempos incial y final. Determinación de la pendiente de la gráfica velocidad en función del tiempo.

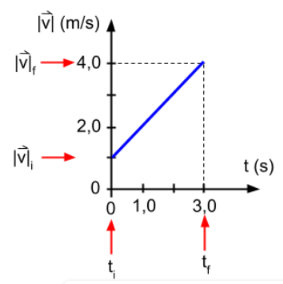
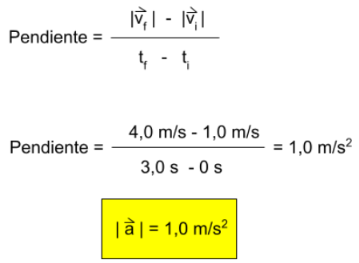
La aceleración del movimiento es constante, la representación gráfica de la aceleración en función del tiempo es:

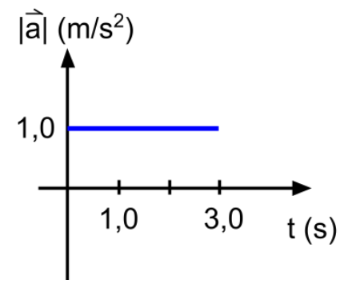
gráfica del módulo de la aceleración en función del tiempo.

7. Representación gráfica de algunos movimientos rectilíneos

A modo de resumen, en los videos de los subcapítulos siguientes, podrás tener el registro de las gráficas características de los movimientos rectilíneos uniforme y uniformemente acelerados.

Para hacer los videos se usó el simulador que ya trabajaste.

7.1. Gráficas del MRU

En los videos a continuación se fijaron ciertas condiciones iniciales. Observa los vectores y cómo es la forma de las curvas en cada una de las gráficas. Te recomiendo que registres en tu cuaderno cada situación.

Situación 1

posición inicial - 4 m,
velocidad inicial: 5 m/s horizontal y a la derecha,
aceleración: 0 m/s².

Se selecciona mostrar los vectores velocidad y aceleración.

Situación 2

posición inicial 4 m,
velocidad inicial: 5 m/s horizontal y a la izquierda,
aceleración: 0 m/s².

Se selecciona mostrar los vectores velocidad y aceleración.

7.2. Gráficas del MRUA: módulo de la velocidad en aumento

En los videos a continuación se fijaron diferentes condiciones iniciales y en todos se seleccionó mostrar los vectores velocidad y aceleración. Observa cómo se van modificando los vectores y cómo es la forma de las curvas en cada una de las gráficas. Te recomiendo que registres en tu cuaderno cada situación.

Situación 1

posición inicial 0 m,
velocidad inicial: 0 m/s horizontal y a la derecha,
aceleración: 5 m/s², horizontal y a la derecha.

Situación 2

posición inicial -6 m,
velocidad inicial: 0 m/s horizontal y a la derecha,
aceleración: 5 m/s², horizontal y a la derecha.

Situación 3

posición inicial 0 m,
velocidad inicial: 0 m/s horizontal y a la derecha,
aceleración: 5 m/s², horizontal y a la izquierda.

Situación 4

posición inicial 6 m,
velocidad inicial: 0 m/s horizontal y a la derecha,
aceleración: 5 m/s², horizontal y a la izquierda.

7.3. Gráficas del MRUA: módulo de la velocidad disminuye y luego aumenta

En los videos a continuación, se fijaron las condiciones iniciales de forma tal que el módulo de la velocidad del hombre disminuye y luego aumenta y además se seleccionó mostrar los vectores velocidad y aceleración. Observa cómo se van modificando los vectores y cómo es la forma de las curvas en cada una de las gráficas. Te recomiendo que registres en tu cuaderno cada situación.

Situación 1

posición inicial 0 m,
velocidad inicial: 6 m/s horizontal y a la izquierda,
aceleración: 5 m/s², horizontal y a la derecha.

Situación 2

posición inicial 0 m,
velocidad inicial: 6 m/s horizontal y a la derecha,
aceleración: 5 m/s², horizontal y a la izquierda.

8. Repaso de la determinación de la pendiente de un gráfico

Para recordar cómo se determina la pendiente de un gráfico te recomiendo que mires el siguiente video:

9. Créditos

Bibliografía consultada:

Hewitt, P. (2007). Física conceptual. México: Pearson-Addison Weasley.
Alvarenga, B., Máximo, A. (1997). Física general. México: Oxford University.

Audio utilizado en los videos:

Apoxode (s.f.). "Stasis chamber" audio en línea en: dig.ccmixter (http://dig.ccmixter.org/film). Licencia CC BY 3.0.

Las imágenes utilizadas fueron tomadas de:

Sistema de referencia - vector posición: Automóvil escarabajo azul. Autor: Open Clipart - Vectors / 27452. Licencia: Dominio público CC0
Rapidez y velocidad: Colourful web buttons set Free Vector. Autor: Diseñado por Freepik. Licencia: CC BY-SA 3.0 Gratis para uso comercial con atribución al autor.
Clker-Free-Vector-Images (17 de junio de 2014). Hombre caminando. En Pixabay. Licencia de Pixabay. Recuperado de https://pixabay.com/es/vectors/hombre-caminar-persona-masculina-308923/

Videos, páginas y simuladores utilizados:

Sistema de referencia - Vector posición: "Cinemática 3D: Sistema de referencia". Autor: Cinematik 3D. Licencia YouTube estándar. Recuperado de: https://www.youtube.com/watch?v=18F3bqyWBqk&index=2&list=PL9ziFjhYuYsdEJhv0IVOT8hBeYi6LiDfx
Trayectoria, distancia y desplazamiento: "Cinemática 3D: Trayectoria, Distancia y Desplazamiento". Autor: Cinematik 3D. Licencia YouTube estándar. Recuperado de: https://www.youtube.com/watch?v=kXa3BRRdIH8&list=PL9ziFjhYuYsdEJhv0IVOT8hBeYi6LiDfx&index=3
Trayectoria, distancia y desplazamiento: "Juego: distancia y desplazamiento". Autor: Peñas, J.; Educaplus. Licencia: Derechos reservados.
Rapidez y velocidad: "Cinemática 3D: Rapidez y Velocidad". Autor: Cinematik 3D. Licencia YouTube estándar. Recuperado de: https://www.youtube.com/watch?v=ATaQ2JD5fd0
Aceleración: "Cinemática 3D: Aceleración". Autor: Cinematik 3D. Licencia YouTube estándar. Recuperado de: https://www.youtube.com/watch?v=htGlherjPmQ&list=PL9ziFjhYuYsdEJhv0IVOT8hBeYi6LiDfx&index=5
Movimiento Rectilíneo Uniforme: "Simulador PhET: El hombre móvil". Autores: Adams, W.; Perkins, K.; Reid, S.; Wieman, C. y Harlow, D. Licencia: CC BY 4.0.
Movimiento Rectilíneo Uniformemente Acelerado: "Simulador PhET: El hombre móvil". Autores: Adams, W.; Perkins, K.; Reid, S.; Wieman, C. y Harlow, D. Licencia: CC BY 4.0.
Determinación de la pendiente de un gráfico: "Calcular la pendiente de una línea recta". Autor: Lfokp. Licencia YouTube estándar. Recuperado de: https://www.youtube.com/watch?v=kCgD6VZNa-M

Autoría del Módulo: Profesora Silvia Pedreira.

spedreira@uruguayeduca.edu.uy

Esta obra está bajo una Licencia Creative Commons Atribución 4.0 Internacional.

Portal Uruguay Educa.
Julio de 2017. Actualizado Mayo 2021.