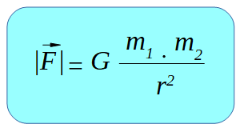Imprimir el Libro CompletoImprimir el Libro Completo

Interacción gravitatoria

En este libro trabajaremos con la interacción gravitatoria

Sitio: Aulas | Uruguay Educa
Curso: Física - 3º C.B.
Libro: Interacción gravitatoria
Imprimido por: Invitado
Día: viernes, 3 de mayo de 2024, 03:48

Tabla de contenidos

1. Introducción

¿Alguna vez te preguntaste por qué la Tierra gira alrededor del Sol o por qué la Luna gira alrededor de la Tierra?
En estos casos como en todos los sistemas del Universo existen fuerzas de atracción gravitatoria, éstas fuerzas son las que determinan  el movimiento que tienen y mantienen a los cuerpos celestes en sus órbitas. Encontrar una explicación al movimiento de los astros, ha sido desde hace muchos siglos, objeto de estudio de muchos científicos. En la segunda mitad del siglo XVII se realizaron los aportes más importantes, con las investigaciones de Kepler, Halley y Newton.
Newton, expone en su libro "Principios Matemáticos de la Filosofía Natural" un modelo dinámico que puede explicar las trayectorias elípticas de los planetas en sus órbitas, basado en la existencia de atracción gravitatoria.
Newton viendo caer una manzana
Según cuenta la leyenda popular, Newton estaba sentado bajo un manzano cuando se le ocurrió la idea de que la atracción gravitatoria se propaga más allá de la Tierra. Tal vez levantó la vista por entre las ramas del árbol, hasta observar la caída de la manzana y vio la Luna, entonces, tal vez pensó que la fuerza entre la Tierra y la manzana que cae es la misma que tira de la Luna y la obliga a describir una órbita alrededor de la Tierra, observando además la similitud entre la trayectoria que describe un planeta que gira en torno al Sol.
Newton comparó la caída de una manzana con la "caída" de la Luna. Pensó que la Luna se desvía del camino recto que seguiría de no haber una fuerza que actuara sobre ella, es decir, la Luna "cae alrededor" de la Tierra redonda a causa de su velocidad tangencial, observó que como los planetas describen órbitas alrededor del Sol y la Luna alrededor de la Tierra deben ser ejercidas sobre ellos una fuerza, pues de lo contrario sus trayectorias no podrían ser curvas. Al razonar de este modo, Newton admitía que sus Leyes del movimiento o Principios también eran válidas para los cuerpos celestes.

2. Ley de Gravitación Universal

La ley de la gravitación universal plantea que el módulo de la fuerza ejercida entre dos cuerpos de masas {\displaystyle m_{1}} y {\displaystyle m_{2}} separados una distancia r es proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia, es decir:


ecuación de la ley de gravitación universal, el módulo de la fuerza gravitatoria es igual a la constante de gravitación universal G por el producto de las masas de los cuerpos que interactúan dividido la distancia que separa los cuerpos al cuadrado.


Se indica que el símbolo del módulo de la fuerza corresponde al módulo de la fuerza de interacción entre los cuerpos de masas m1 y m2. En la figura se representa F1/2 (con flecha arriba de la F) a la fuerza ejercida por el cuerpo 1 sobre el 2 y F2/1 (con flechita arriba de la F) a la fuerza ejercida por el cuerpo dos sobre el 1. La unidad de medida de la fuerza en el S.I. es el Newton (N). La dirección de las fuerzas es igual a la dirección de la recta que une ambos cuerpos. Que m1 y son los valores de las masas de los cuerpos. La unidad de medida en el S.I. para la masa es el kilogramo (kg). Que r es la distancia que separa los cuerpos. La unidad de medida en el S.I. es el metro (m). En la ecuación este valor está elevado al cuadrado. Que Ges la constante de Gravitación Universal, su valor no pudo ser determinado por Newton, pero predijo de debía ser un valor muy pequeño. Cavendish fue el primero que intentó determinarla en 1798, hoy en día el valor más preciso al que se ha llegado es: G = 6,67384 x 10-11 N.m2/kg2


3. Aceleración Gravitatoria

Si consideramos la interacción entre la Tierra de masa M = 5,97 × 1024 kg y radio promedio de  r = 6,37 x 106 m y un objeto cualquiera ubicado en su superficie de masa m. Al plantear la Ley de Gravitación Universal:

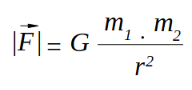
ecuación de gravitación universal: módulo de la fuerza gravitatoria es igual a la constante de gravitación universal por el producto de las masas de los cuerpos que interactúan dividido la distancia que los separa elevada al cuadrado.

para la interacción entre la Tierra y el objeto de masa m:

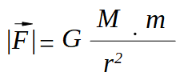
ecuación de gravitación universal: módulo de la fuerza gravitatoria es igual a la constante de gravitación universal por el producto de la masa de la Tierra M por la masa del otro cuerpo, dividido la distancia que los separa elevada al cuadrado.

Dado que G (Constante de Gravitación Universal), M (masa de la Tierra) y r (radio de la Tierra) son valores constantes podemos agruparlos en una nueva constante que llamaremos |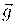 \vec{g} |:

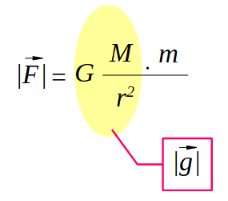
ecuación de gravitación universal: módulo de la fuerza gravitatoria es igual a la constante de gravitación universal por el producto de la masa de la Tierra M por la masa del otro cuerpo, dividido la distancia que los separa elevada al cuadrado. Se indica con un círculo amarillo que la constante de gravitación universal por la masa de la Tierra dividido el rario de la Tierra al cuadrado corresponde al módulo de la aceleración gravitatoria.

Reescribiendo la ecuación y reordenándola, obtenemos:

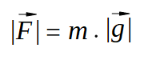
módulo de la fuerza gravitatoria es igual a la masa del cuerpo por el módulo de la aceleración gravitatoria.

La aceleración que experimenta un cuerpo cerca de la superficie terrestre:

cálculo de la aceleración gravitatoria usando la constante de gravitación universal multiplicada por la masa de la Tierra y dividido entre el radio terrestre.

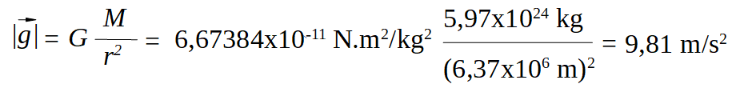
Por tanto el módulo de la aceleración gravitatoria es:

módulo de g igual a 9,81 metros por segundo al cuadrado

Observemos la similitud entre el Principio de Masa y  la expresión obtenida para la interacción gravitatoria entre la Tierra y un cuerpo cualquiera cercano a su superficie de masa m:

vector fuerza es igual a la masa por el vector aceleración y el vector fuerza igual a la masa por la aceleración gravitatoria.

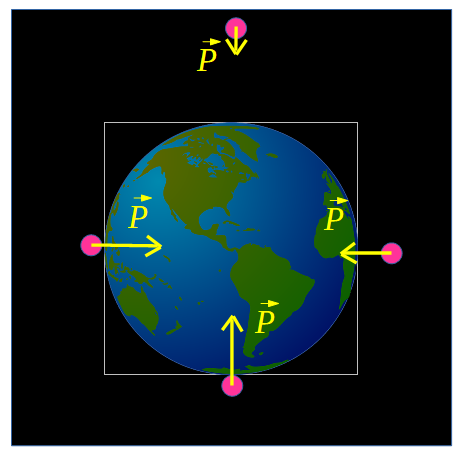
Por tanto la Fuerza de atracción que ejercerá la Tierra sobre un objeto cualquiera, se llama peso y  tendrá un módulo que es el producto entre su masa y 9,81 m/s2, dirección radial y apuntando hacia el centro de la Tierra.

Pelota ubicada a diferentes distancias de la superficie terrestre. El peso está representado en cada una de ellas mostrando la diferencia de tamaño con la distancia a la superficie

4. Video

Hace muchos años, un actor mexicano apodado “Cantinflas”, hacía películas muy divertidas. Invita a las personas más grandes que vivan contigo a mirar este fragmento de una película de ese actor. Se van a divertir un rato juntos y podrás aprovechar la oportunidad para explicarle a los demás en qué consiste la Ley de Gravitación Universal:

Actividad tomada de: http://aulasvirtuales2.ces.edu.uy/pluginfile.php/9053/mod_resource/content/1/actividad_8__ley_de_gravitacin_universal.html

5. Créditos

Bibliografía consultada:

  • Hewitt, P. (2007). Física conceptual. México: Pearson-Addison Weasley. 
  • Alvarenga, B., Máximo, A. (1997). Física general. México: Oxford University.


Las imágenes utilizadas fueron tomadas de:

  • Introducción: Newton's apple. Autor: Borek, A. Licencia: CC BY -SA 4.0.
  • Ley de gravitación Universal: Dos cuerpos atrayéndose con las fuerzas representadas. Autor: Pedreira, S. Licencia: CC BY - SA 4.0
  • Aceleración gravitatoria: Planeta Tierra. Autor: Clker-Free-Vectors-Images/29611. Licencia: Dominio Público CC0
  • Aceleración gravitatoria: Pelota ubicada a diferentes distancias de la superficie terrestre con el peso representado en cada una de ellas.  Autor: Pedreira, S. Licencia: CC BY -SA 4.0


Videos, páginas y simuladores utilizados:


Autoría del Módulo: Profesora Silvia Pedreira.

spedreira@uruguayeduca.edu.uy


Esta obra está bajo una Licencia Creative Commons Atribución 4.0 Internacional. 

Portal Uruguay Educa.
Julio de 2017. Actualizado Marzo de 2020.