¿Cómo calculamos el calor?
-
| Sitio: | Aulas | Uruguay Educa |
| Curso: | Ciencias Físicas - 2º C.B. |
| Libro: | ¿Cómo calculamos el calor? |
| Imprimido por: | Invitado |
| Día: | jueves, 3 de abril de 2025, 23:58 |
1. Calorímetro
El calorímetro es un instrumento de laboratorio que permite cuantificar la cantidad de calor liberada o absorbida por un sistema en un determinado proceso.
Se utiliza para estudiar la relación entre el calor suministrado a un sistema y su variación de temperatura, o el calor de un proceso y su variación de temperatura.


Figuras 1 y 2. Imagen del interior y exterior de un calorímetro utilizado en los liceos.
El calorímetro está formado por:
- Un recipiente con tapa construido de material aislante, por ejemplo espumaplast.
- Una fuente térmica que suministre energía; generalmente se utiliza un resistor conectado a un generador de corriente eléctrica, cuando la corriente eléctrica pasa por el resistor, éste transfiere energía por calor al sistema.
- Un termómetro para medir las temperaturas del líquido (generalmente agua) o del sistema contenido en el recipiente.
Las siguientes imágenes muestran un corte longitudinal de dos calorímetros (con y sin resistor) de uso común en un laboratorio, en ellas se muestran sus partes fundamentales:
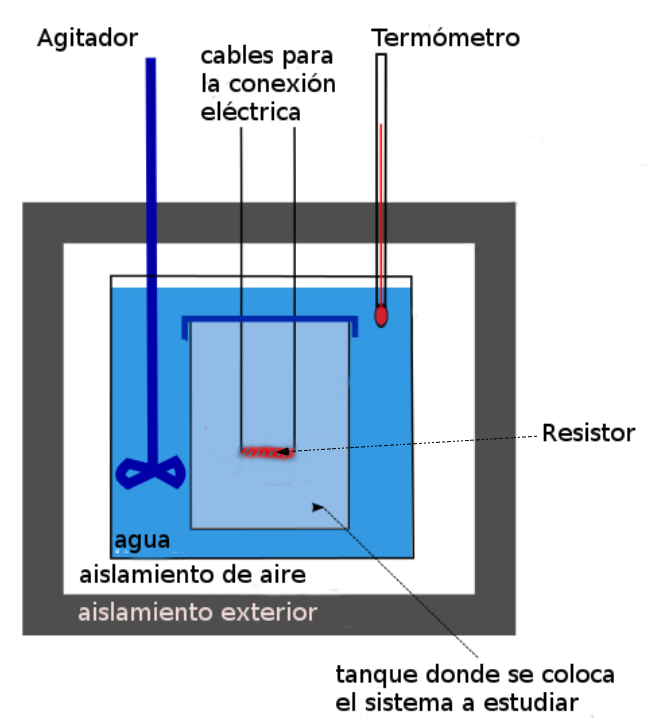
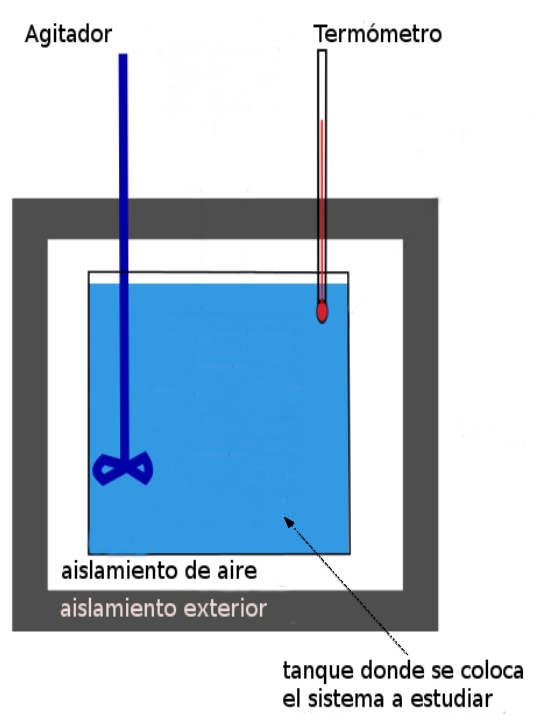
Figura 3. Corte longitudinal de calorímetro con resistor. Figura 4. Corte longitudinal de calorímetro sin resistor.
2. Relación entre calor y variación de temperatura
A partir de datos experimentales se puede concluir que el calor es directamente proporcional a la variación de temperatura.
La variación de temperatura, se determina haciendo la temperatura final menos la temperatura temperatura inicial (Δt = tfinal - tinicial).
PODEMOS REPRESENTAR DICHA RELACIÓN CON LA CONSTRUCCIÓN DE LA SIGUIENTE GRÁFICA:
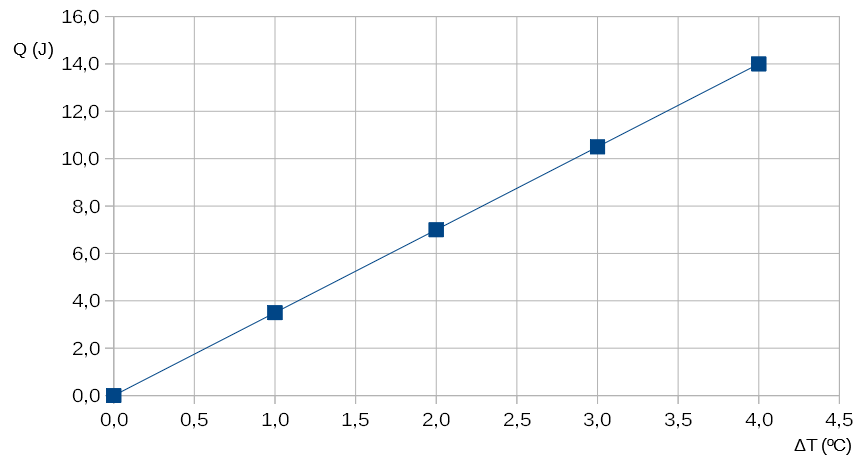
Figura 5 . Gráfico de Calor en función de la variación de temperatura.
3. Relación entre calor y masa
A partir de datos experimentales se puede concluir que el calor es directamente proporcional a la masa.

PODEMOS REPRESENTAR DICHA RELACIÓN CON LA CONSTRUCCIÓN DE LA SIGUIENTE GRÁFICA:
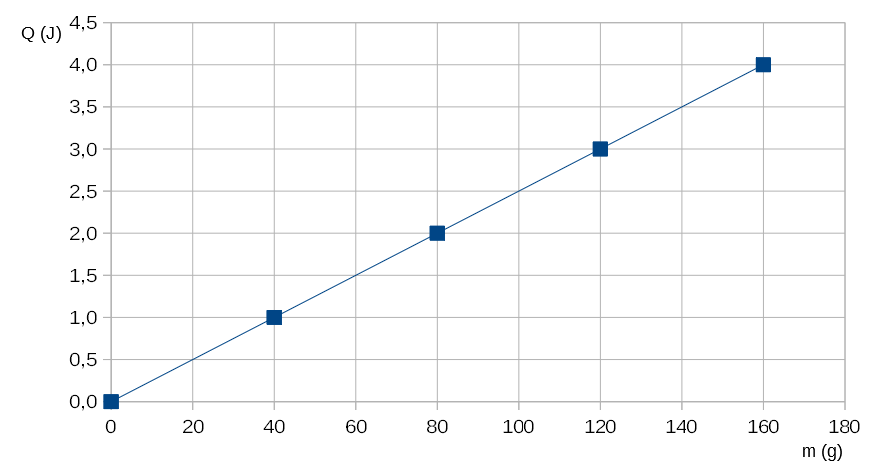
Figura 6. Gráfico de Calor en función de la masa.
4. Calor específico
A partir de los puntos trabajados en los capítulos anteriores, sabemos que: Q α Δt y también lo es a la masa, por lo tanto el cociente entre el calor y (m . ΔT) tiene un valor constante.
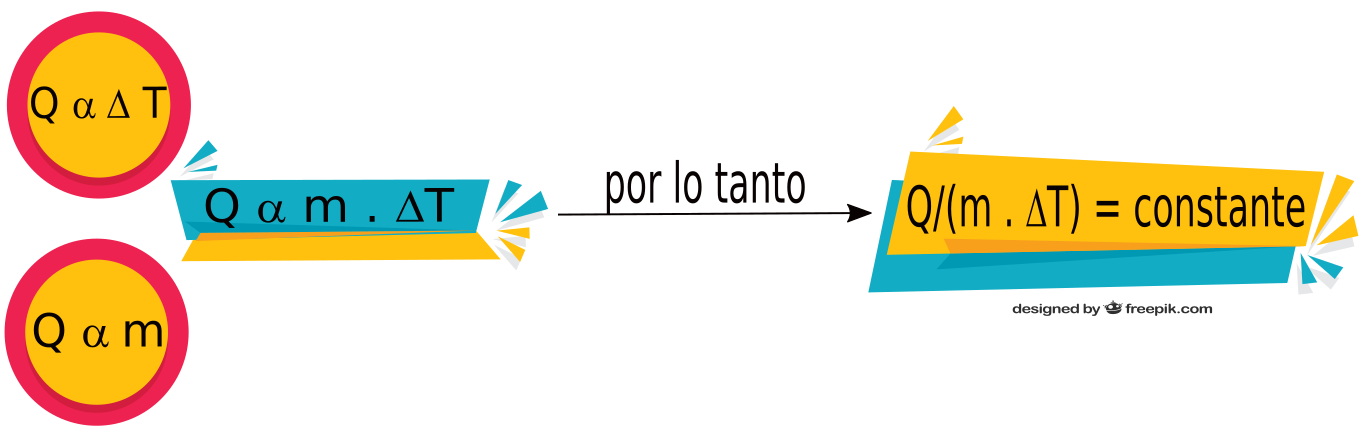
El valor constante que se obtiene al hacer el cociente Q/(m . ΔT ), es diferente para cada sustancia o material, y es una propiedad intensiva característica denominada Calor Específico. La notación que se utiliza para denominar al Calor Específico es Ce.

El calor específico de una sustancia o material, cuya notación es "Ce", es la cantidad de energía que hay que suministrar a 1 gramo de la misma para que su temperatura aumente 1 °C.
Las unidades más utilizadas del calor específico son: J/g°C o cal/g°C
5. Tabla de calores específicos
|
Sustancia o Material |
Ce (J/g°C) |
Ce (cal/g°C) |
|---|---|---|
|
Agua |
4,180 |
1,000 |
|
Hielo |
2,215 |
0,530 |
|
Etanol |
2,508 |
0,600 |
|
Cobre |
0,389 |
0,093 |
|
Plata |
0,233 |
0,056 |
|
Aluminio |
0,944 |
0,226 |
|
Hierro |
0,456 |
0,109 |
|
Platino |
0,134 |
0,032 |
|
Oro |
0,130 |
0,031 |
6. ¿Cómo se determina la transferencia de energía por calor?
Se puede determinar el intercambio de energía por calor que experimenta un cuerpo sabiendo su temperatura inicial y final, su masa y el calor específico del material que forma el cuerpo. El calor se calcula con la siguiente ecuación:

Siendo: Q → calor absorbido o liberado por el cuerpo
m → masa del cuerpo
Ce → calor específico (valor característico para cada sustancia o material)
ΔT = Tf - Ti → variación de temperatura (temperatura final menos temperatura inicial)
Para tener en cuenta:
- si el sistema absorbe energía, la temperatura del cuerpo aumenta, es decir la temperatura final es mayor que la inicial, por lo tanto la ΔT es positiva y el Q es positivo: ΔT > 0 → Q > 0.
- si el sistema libera energía, la temperatura del cuerpo disminuye, es decir la temperatura final es menor que la inicial, por lo tanto Δt es negativa y el Q es negativo. ΔT < 0 → Q < 0.
Usando la misma ecuación pero operando matemáticamente se pueden determinar las magnitudes masa, calor específico o variación de temperatura, según se desee y dependiendo de los datos experimentales que se tengan.
El siguiente esquema te ayudará a calcular la magnitud que corresponda según los datos, también se aclara la unidad de cada una:
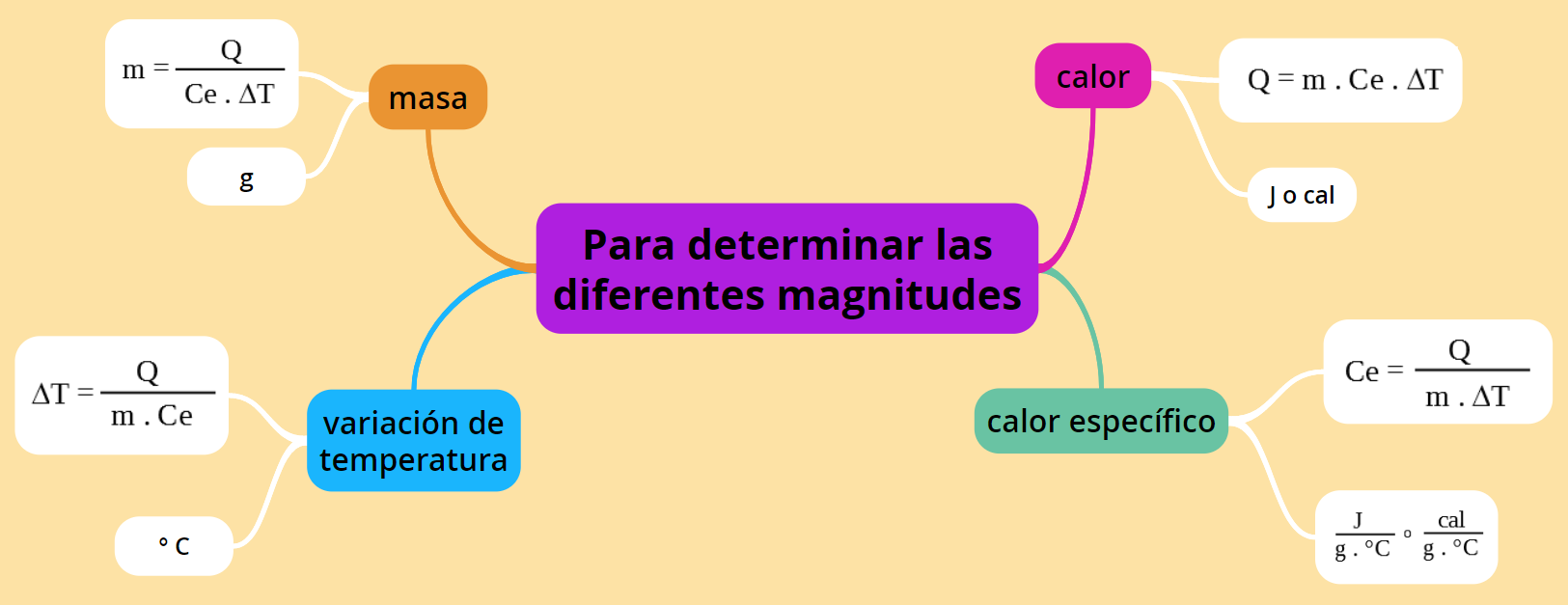
La tabla a continuación contiene la misma información del esquema en otro formato:
|
Magnitud |
Ecuación |
Unidades |
|---|---|---|
|
Calor (Q) |
Q = m . Ce . ∆T
|
J o cal |
|
Calor específico (Ce) |
Ce = Q/m.∆T
|
J/g°C o cal / g°C |
|
Masa (m) |
m = Q/Ce .∆T |
g |
|
Variación de temperatura (∆T) |
∆T = Q/ m. Ce
|
°C |
7. Ejemplos de resolución de ejercicios
Ejemplo 1:
Determinar el calor que absorbe una moneda de cobre (Ce = 0,385 J/g.°C), de masa 3,25 g, si su temperatura se eleva desde 5,0 °C hasta 30,0 °C.
Resolución:
- Como nos pide que determinemos el Q, usaremos la ecuación: Q = m . Ce . ΔT, y sabemos que ΔT= Tf - Ti
- Identificamos los datos que nos da la letra:
Ce = 0,385 J/g.°C
m = 3,25 g
Ti = 5,0 °C
Tf = 30,0 °C
- Sustituimos los valores en la ecuación: Q = 3,25 g . 0,385 J/g.°C . (30,0 °C - 5,0 °C) = 31,3 J
- Luego de realizar la operación el valor del calor absorbido por la moneda es de 31,3 J, este valor es positivo porque la moneda aumentó su temperatura.
Ejemplo 2:
Se le suministran 30,00 kcal a una cierta masa de agua, su temperatura aumenta de 5,00 °C a 30,00 °C. Determinar el valor de la masa de agua usada en el experimento.
Resolución:
- Como nos pide que determinemos la masa, usaremos la ecuación: m = Q/Ce . ΔT
- Identificamos los datos que nos da la letra del ejercicio:
Q = 30 kcal, el valor que está en kcal lo tenemos que pasar a cal, por lo tanto Q = 30.000 cal
Ti = 5,0 °C
Tf = 30,0 °C
- El valor de Ce del agua lo sacamos de la tabla de Calores Específicos vista anteriormente: Ce = 1,00 cal/g . °C
- Sustituimos los valores en la ecuación: m = 30.000 cal / [1,000cal/g . °C . (30,00 °C - 5,00 °C)] = 1.200 g
- Luego de realizar la operación, determinamos que la masa de agua usada fue de 1.200 g o 1,2 kg.
De igual forma se procede si se pide cualquiera de las otras magnitudes.
8. Créditos
Bibliografía consultada:
- Segurola, B; Saravia, G; Szwarcfiter, M; Amoedo, A. y Uzal, C. (2010). Ciencias Físicas 2. Montevideo, Uruguay: Contexto.
- Ferreira, D; Menéndez, M. (2012). Ciencias Físicas 2º. Uruguay: Textos del Sur.
- Franco, R; López Arriazu, F.; Serafini, G et al (2008). Física y química. Intercambios de energía. Estructura y transformación de la materia. Argentina: Santillana.
- Hewitt, P. (2007). Física Conceptual. México: Addison Wesley Longman.
- Alvarenga, B., Máximo, A. (1997). Física general. México: Oxford University.
Las imágenes utilizadas fueron tomadas de:
- Calorímetro. Autor: Lanzi. Licencia: Dominio Público CC0, vía Wikimedia Commons.
- Calorímetro de laboratorio. Autor: Anarella Gatto. Licencia: CC BY-SA 4.0.
- Banners de origami de rebajas. Autor: Freepik. Licencia: CC BY-SA 3.0.
- Colorful origami sale banner collection. Autor: Freepik. Licencia: CC BY-SA 3.0.
- Pack of geometric lower thirds. Autor: Freepik. Licencia: CC BY-SA 3.0.
- Collection of abstract infographic banners. Autor: Freepik. Licencia: CC BY-SA 3.0.
- Ecuaciones relacionadas con el calor. Autor: Silvia Pedreira. Licencia: CC BY-SA 3.0
Autoría del Módulo: Profesoras Anarella Gatto y Silvia Pedreira.
agatto@uruguayeduca.edu.uy
spedreira@uruguayeduca.edu.uy
Esta obra está bajo una Licencia Creative Commons Atribución 4.0 Internacional.
Portal Uruguay Educa.