¿Qué es la densidad?
En este libro estudiarás sobre la densidad, propiedad intensiva característica de la materia.
| Sitio: | Aulas | Uruguay Educa |
| Curso: | Ciencias Físicas - 1º C.B. |
| Libro: | ¿Qué es la densidad? |
| Imprimido por: | Invitado |
| Día: | jueves, 6 de marzo de 2025, 23:40 |
1. ¿Qué es la densidad?
Si comparamos un cubo de madera y otro de hierro de 10 cm de arista cada uno, podemos decir que ambos tienen igual volumen pero diferente masa.
Obviamente la masa del cubo de hierro es mayor que la del cubo de madera. Decimos entonces que el hierro es más denso que la madera.
Las masas de las partículas y las distancias entre ellas determinan la densidad de los materiales.
La densidad es una medida de cuán compacta es la materia, cuánta masa ocupa un determinado volumen.
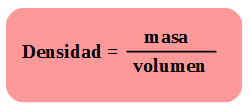
La unidad de densidad en el Sistema Internacional es el kg/m3.
Otra unidad de uso común es el g/cm3.
La equivalencia g/cm3 - kg/m3 es:
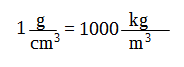
La densidad es una propiedad de la materia que no depende de la masa, es decir, 1 kg de plomo tiene la misma densidad que 2 kg de plomo.
Si consideramos otra sustancia, por ejemplo el aluminio, tiene una densidad diferente de la del plomo.
Cada sustancia o material tiene su densidad característica y por lo tanto es posible identificarla y diferenciarla de otra si sabemos su densidad.
Recuerda las equivalencias de unidades de volumen:
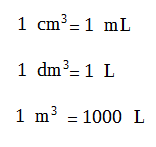
2. Valores de densidad de algunos materiales
En la siguiente tabla podrás observar que las densidades cambian según de qué material se trate:
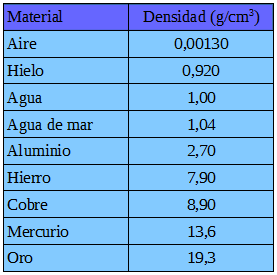
3. Comparamos la densidad de diferentes materiales
Un corcho flota en el agua, porque la densidad del corcho es menor que la del agua.
Un tornillo de hierro y la cuchara se hunden en el agua, porque la densidad de su material es mayor que la del agua.

¿Podemos afirmar que siempre que un cuerpo flota en otro, es menos denso? Veamos dos ejemplos:
1)


El metal que forma el clip y el que forma la hoja de afeitar tienen mayor densidad que el agua, sin embargo flotan. Estos objetos flotan porque sobre la superficie del agua actúan fuerzas (tensión superficial) que impiden que se sumerjan, pero si movemos el agua ambos objetos se hundirán.
2) Los aviones y los pájaros suben, bajan o se suspenden en el aire siendo su densidad mucho mayor que la del aire.
Esto es posible porque tanto los aviones como los pájaros realizan movimientos, es decir mueven el aire a su alrededor lo que permite que se mantengan en el aire.
Por tanto que un objeto flote en otro, no garantiza que su densidad sea menor.
Debemos mejorar la idea, en vez de decir que un cuerpo es menos denso cuando flota en otro, deberíamos decir que si un objeto es capaz de ascender en un líquido o en un gas y mantenerse en esa posición sin que exista movimiento relativo entre el objeto y el líquido o el gas, entonces el objeto será menos denso que el líquido o el gas que lo rodea.

El material de la cometa es más denso que el aire, debido a que el aire se mueve alrededor de la cometa ésta se mantiene en el aire.
Al introducir aceite en agua, podemos observar como las gotas tienden a subir y ubicarse en la superficie del agua, la densidad del aceite es menor que la del agua, el aceite asciende por el agua y se ubica sobre su superficie.

5. Gráficas
En la mayoría de los trabajos científicos, experimentos, el uso de las gráficas es una herramienta de gran utilidad. Porque permiten visualizar fácilmente y de forma simultánea todos los datos. Además permiten establecer relaciones entre las magnitudes graficadas.
En la mayoría de los casos el valor de la pendiente o el valor del área bajo la curva representan alguna magnitud física que es importante para el experimento.
Es posible también encontrar valores por interpolación y extrapolación aunque no los hayamos medido.
En este libro hemos trabajado con las magnitudes masa y con el volumen de un cuerpo, a estas magnitudes se les llama variables.
Variable Independiente: es la variable que se elige de forma arbitraria, su valor no va a depender de otra variable.
Variable Dependiente: su valor depende del valor de otra variable, generalmente la variable independiente.
El volumen es la variable elegida arbitrariamente, por tanto es la variable independiente, y la masa es la que resulta de la otra variable (el volumen) y por tanto es la dependiente.
5.1. Organización de los datos en un experimento
Para realizar el gráfico usaremos los ejes cartesianos x - y, donde:
- el eje x es el eje de las abscisas donde se coloca la variable independiente (el volumen, V, en este caso) y
- en el eje y, llamado eje de las ordenadas se coloca la variable dependiente (la masa, m, en este caso).
Se construye una tabla de valores con los datos experimentales, colocando en la primera columna la variable independiente (la que se colocará en el eje x) y en la segunda columna la variable dependiente (la que se colocará en el eje y) por ejemplo:
|
V (mL) |
m (g) |
|
5,00 |
13,5 |
|
10,00 |
27,0 |
|
15,00 |
40,5 |
|
20,50 |
55,3 |
|
26,00 |
70,2 |
En el encabezado de cada columna se coloca el símbolo de la magnitud y entre paréntesis la unidad de medida que se utilizó al realizar la medida, o el correspondiente múltiplo o submúltiplo de dicha unidad.
Luego realizaremos la gráfica de masa en función del volumen, que se escribe de la siguiente forma: m = f(V). Siendo la m (masa) la variable dependiente, el V (volumen) la variable independiente y la f se lee como "en función de".
En la gráfica debemos trazar los ejes cartesianos, x e y, perpendiculares entre sí. Para realizar esta parte es necesario utilizar instrumentos de geometría, papel cuadriculado o milimetrado lápiz y goma.
En el extremo derecho del eje x así como en el extremo superior del eje y debemos indicar con su símbolo la magnitud graficada y entre paréntesis la unidad de medida de la misma.
La gráfica carecería de significado si no indicamos claramente las magnitudes que queremos relacionar con ella.
Mira la figura que sigue:
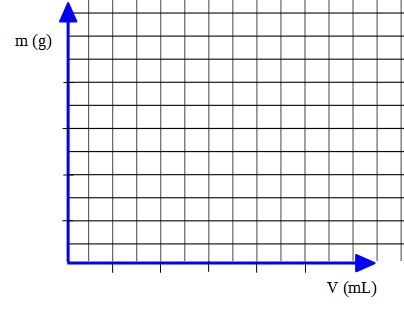
Luego tenemos que elegir una escala adecuada para representar los valores de las magnitudes. La elección de la escala es esencial, ya que los puntos no pueden quedar muy juntos, los ejes además deben medir en centímetros aproximadamente la misma longitud. Es importante tener en cuenta que los puntos que resulten en el gráfico no deben unirse con líneas rectas.
Se debe tratar, que el gráfico ocupe la mayor parte de la hoja de cuadriculada o milimetrada. Se sugiere elegir escalas que puedan subdividirse fácilmente.
Los valores recomendados son 1, 2, 5 y 10. No se recomiendan escalas múltiplos de 3, 7, 6 y 9 debido a que es difícil ubicar los valores y dificultan la lectura de los mismos en el gráfico.
Se puede elegir una escala diferente para cada eje, es decir, para cada magnitud.
En algunos casos no es necesario que la gráfica empiece su escala en cero.
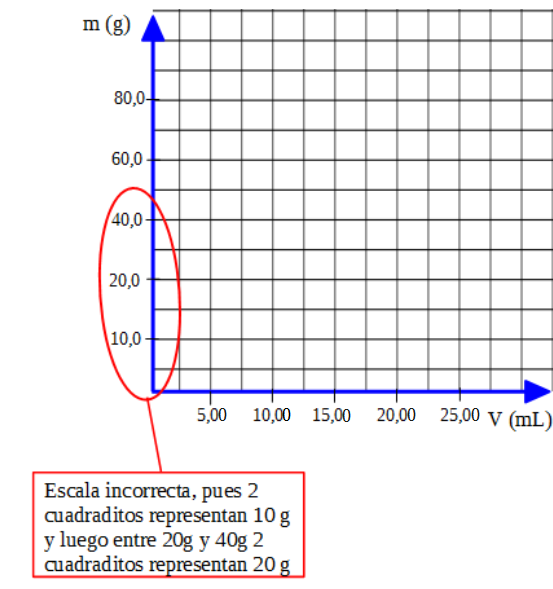
Se debe tener en cuenta que cuando elegimos una escala todos los intervalos en dicha escala tienen que tener el mismo valor, como se ve en la figura que sigue:
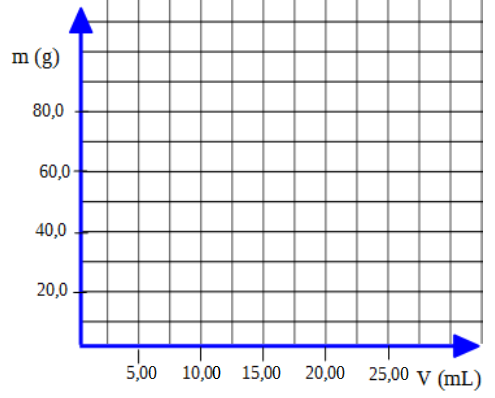
Luego que tenemos la escala indicada en cada uno de los ejes, procedemos a colocar los puntos que corresponden a cada par de medidas de volumen y masa.
Para este ejemplo: Buscamos en el eje del V (mL) el valor que correspondiente a 5,0 mL y en el eje de la m (g) el valor que corresponde a 13,5 g, ayudándonos con las líneas cuadricualdas auxiliares del papel (si el papel no es cuadriculado tenemos que trazar esas líneas utilizando líneas punteadas), en el lugar que se cruzan dichos valores ubicamos el punto.
Repetimos el procedimiento con el resto de los pares de valores:
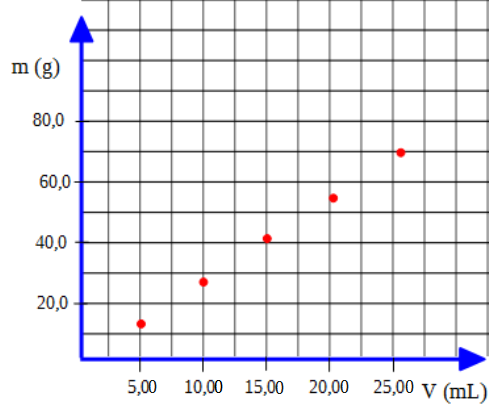
Luego trazamos la curva que se genera con los puntos, en este caso se trata de una recta:
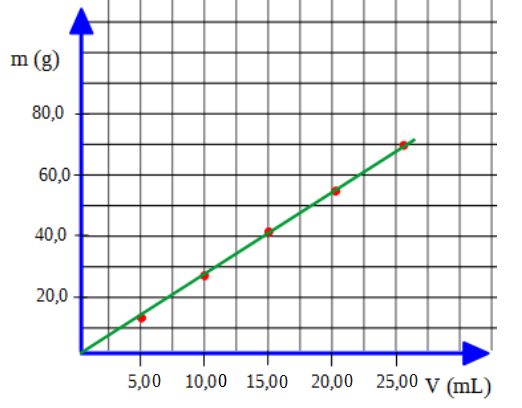
La curva de la gráfica puede no ser una recta, podría ser una parábola, hipérbola, etc.
El trazado de la curva se hace con una línea continua que pase por la mayor cantidad de puntos posible, aunque no pase por todos.
Es importante tener en cuenta que la curva de la gráfica es una línea continua, no es correcto unir cada par de puntos quedando así segmentos unidos.
5.2. Interpretación de una gráfica
La interpretación de las gráficas que surgen de los datos experimentales es muy importante en todas las ciencias y también en la vida cotidiana.
Por ejemplo en el recibo de UTE y OSE vienen gráficas de "consumo de energía" y de agua, en función del mes y se compara también con el consumo del año anterior.
Realizaremos el análisis e interpretación de una gráfica como la obtenida en este experimento, es decir una recta que pasa por el origen de coordenadas.
En el experimento que realizamos, medimos volumen y masa de cuerpos formados por la misma sustancia, al graficar obtuvimos una recta que pasa por el origen de coordenadas, esto significa que las magnitudes graficadas son directamente proporcionales.
Significa esto que si la variable independiente (el volumen en nuestro ejemplo) aumenta o disminuye la variable dependiente (la masa en nuestro ejemplo) aumenta o disminuye en la misma proporción.
| V (mL) |
m (g) |
|---|---|
|
5,00 |
13,5 |
|
10,00 |
27,0 |
|
15,00 |
40,5 |
|
20,50 |
55,3 |
|
26,00 |
70,2 |
- Observemos el primer par de valores, la variable independiente (V) es 5,0 mL y la dependiente (m) es 13,5 g,
- si se duplica el V la m también se duplica par de valores (10,0 mL, 27,0 g),
- si se triplica el V = 15,0 mL la masa también se triplica, m = 40,5 g. Es similar si la variable independiente disminuye, la otra variable disminuirá en igual proporción.
Agregamos una columna a la tabla y realizamos el cociente entre la variable dependiente y la variable independiente:
| V (mL) |
m (g) |
m/V (g/mL) |
|---|---|---|
|
5,00 |
13,5 |
2,70 |
|
10,00 |
27,0 |
2,70 |
|
15,00 |
40,5 |
2,70 |
|
20,50 |
55,3 |
2,69 |
|
26,00 |
70,2 |
2,70 |
Observamos que el valor del cociente entre m y V es igual para todos los pares de valores.
A ese valor que resulta de la división se le denomina: constante de proporcionalidad.
En la mayoría de los casos la constante de proporcionalidad tiene algún significado.
En el ejemplo la constante de porporcionalidad corresponde a la densidad de la sustancia utilizada, ya que la
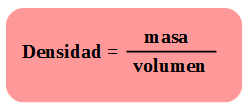
Es importante observar también la unidad que surge al realizar el cociente, eso nos puede dar un indicio de la magnitud que representa la constante de proporcionalidad.
La densidad es una propiedad que permite identificar a una sustancia, si consultamos los valores de las densidades para diferentes sustancias que se encuentran en el capítulo 2 de este libro, verás que una d = 2,7 g/mL corresponde a la densidad del aluminio. Podemos de esta forma saber de qué material son los objetos usados en el experimento.
Para investigar si dos magnitudes son directamente proporcionales podemos:
- Graficar una magnitud en función de la otra, la gráfica que resulte debe ser una recta que pasa por el origen de coordenadas.
- Realizar los cocientes (divisiones) entre la variable dependiente y la independiente, los valores que resulten deben ser siempre constantes. A ese valor constante se le llama constante de proporcionalidad, y generalmente tiene un significado físico.
5.3. Pendiente de una recta
Cuando dos magnitudes son directamente proporcionales al dividirlas podemos determinar la constante de proporcionalidad. También se puede determinar dicha constante a partir de la gráfica, calculando la pendiente de la recta.
- Determinación de la pendiente de una recta
Utilizaremos el mismo ejemplo que en los subcapítulos anteriores para la explicación.
1) Elegimos dos puntos cualesquiera que pertenezcan a la recta.
Al punto que tenga menor valor en el eje de las abscisas le llamaremos inicial (i) y al de mayor valor en el eje de las abscisas le llamaremos final (f).
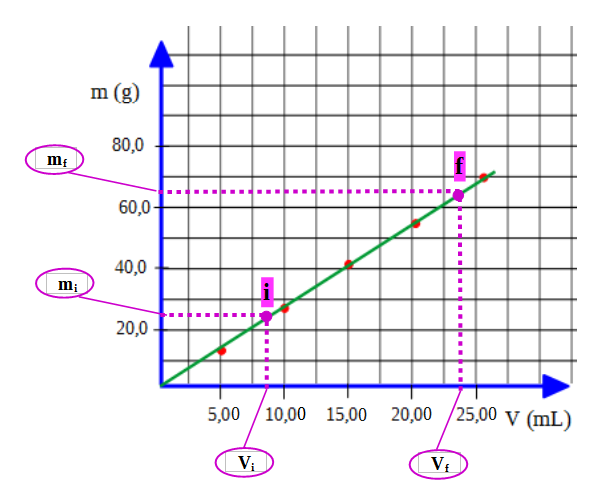
Las coordenadas del punto inicial son: Vi = 8,75 mL, mi = 25,0 g, y las del punto final son: Vf = 23,75 mL, mf = 65,0 g
2) Calculamos las variaciones de cada magnitud: ΔV y Δm. Recuerda que la letra griega delta (Δ) significa variación.
ΔV = Vf - Vi = 23,75 mL - 8,75 mL = 15,00 mL → ΔV = 15,00 mL
Δm = mf - mi = 65,0 g - 25,0 g = 40,0 g → Δm = 40,0 g
3) Cálculo de la pendiente:

En el caso de nuestro ejemplo:

El resultado es:

Podemos observar que la pendiente de la recta es igual a la constante de proporcionalidad que calculamos en el capítulo anterior dentro de un cierto margen de incertidumbre. Por tanto para este ejemplo particular la pendiente de la gráfica representa la densidad de los cuerpos usados para el experimento.
Recuerda que en toda medida siempre hay un margen de incertidumbre.
5.4. Créditos
Bibliografía consultada/Sitios:
- Hewitt, P. (2007). Física conceptual. México: Pearson-Addison Weasley.
- Alvarenga, B. y Máximo, A. (1997). Física general. México: Oxford University.
- Saravia, G; Segurola, B. y Szwarcfiter, M. (1998). Ciencias Físicas I. Uruguay: Ed. Textos del Sur.
- Galagovsky, L. (Diciembre 2007). Del aprendizaje significativo al aprendizaje sustentable. Revista Quehacer Educativo.
Imágenes:
- Comparamos la densidad de diferentes materiales: http://www.clarionweb.es/5_curso/c_medio/cm508/cm50803g.htm
- Comparamos la densidad de diferentes materiales: http://www.ugr.es/~jperez/docencia/Evolver/tutorial6.html
- Comparamos la densidad de diferentes materiales: https://www.ucm.es/data/cont/docs/76-2013-06-11-01_Surface_tension_Objects_on_a_water_surface.pdf
- Comparamos la densidad de diferentes materiales: http://chinalati.com/m/blogpost?id=6466754%3ABlogPost%3A22614
- Comparamos la densidad de diferentes materiales: http://www.elgranporque.com/por-que-no-se-puede-mezclar-aceite-y-agua/
- Repasando m, V y d: http://www.freepik.es/vector-gratis/infografia-con-cuatro-opciones-de-color_1028503.htm
Autoría del Módulo: Profesoras Anarella Gatto y Silvia Pedreira.
agatto@uruguayeduca.edu.uy
spedreira@uruguayeduca.edu.uy
Esta obra está bajo una Licencia Creative Commons Atribución 4.0 Internacional.
Portal Uruguay Educa.
Junio de 2017.
