Trabajo mecánico
En este libro podrás estudiar y entender sobre las transferencias de energía por trabajo.
| Sitio: | Aulas | Uruguay Educa |
| Curso: | Física - 3º C.B. |
| Libro: | Trabajo mecánico |
| Imprimido por: | Invitado |
| Día: | jueves, 3 de abril de 2025, 00:57 |
1. Introducción
Cuando elevamos una carga, estamos realizando un trabajo contra la fuerza de atracción que la Tierra ejerce sobre esa carga. Este trabajo será mayor, cuanto más pesada sea la carga, o cuanto mayor sea la altura a la que se eleve la misma.
La consecuencia que se puede observar de esa transferencia de energía por trabajo, es que el sistema en que la fuerza es aplicada modifica su energía cinética.
Por ejemplo: cuando un resorte que se está deformando o si un cuerpo que se
eleva a cierta altura con respecto a la superficie terrestre se está
produciendo una transferencia de energía por trabajo, pues se está
aplicando una fuerza y el cuerpo se desplaza. En los dos casos los cuerpos cambian su energía.
El caso más sencillo de estudiar es cuando la fuerza es constante, el movimiento se da en una línea recta y en la misma dirección en que actúa la fuerza. En este libro estudiaremos, un poco más adelante, el caso de una fuerza constante que actúa sobre un objeto formando un ángulo con la dirección del movimiento y luego el caso particular en que la fuerza y el desplazamiento tienen igual dirección y sentido.
1.1. Ejemplo
En este ejemplo se estudia en qué partes del levantamiento de las pesas el deportista realiza trabajo sobre las mismas. En el ejemplo se utiliza la imagen de Óscar Figueroa, primer medalla de oro varonil en la historia de Colombia en los Juegos Olímpicos de Río de Janeiro 2016.

En 1. Óscar se concentra y se prepara para realizar el primer movimiento, en ese intervalo de tiempo no realiza trabajo sobre las pesas, pues las pesas no se desplazan de su posición. Si se toma como sistema de referencia el piso, la pesas no tienen Epg (no tienen altura con respecto al sistema de referencia) ni tienen Ec (están en reposo).
En la foto 2. está realizando un desplazamiento desde la posición de la foto 1. hasta la posición de la foto 3, para realizar ese desplazamiento aplica fuerza sobre las pesas. En esta situación sí realiza trabajo sobre las pesas, ya que sobre ellas está aplicada la fuerza que realiza Óscar que produce que las pesas se muevan. Podemos decir aquí que hubo una transferencia de energía por trabajo ya que las pesas adquieren Ec (se mueven) y se elevan con respecto al piso (sistema de referencia) por lo que tienen también Epg.
En la foto 3. las pesas se encuentran en reposo sobre los hombros del deportista, mientras las pesas permanecen en reposo Óscar aplica fuerza sobre las pesas, pero ellas no se mueven, por lo que no realiza trabajo sobre las pesas. Aquí las pesas no cambian ni su Ec ni su Epg. Óscar se cansa mientras las sostiene, pero como las pesas no se mueven, aunque él haga fuerza, no realiza trabajo sobre las mismas. Se realiza trabajo sobre los músculos, que se estiran y contraen (fuerza por la distancia) en escala biológica, pero ese trabajo no es realizado sobre las pesas.
En la foto 4. está realizando un desplazamiento desde la posición de la foto 3. hasta la posición final en la foto 5, en ese intervalo aplica fuerza sobre las pesas y ellas se desplazan. Por tanto, en esta situación sí está realizando trabajo sobre las pesas. También hay transferencia de energía por trabajo: las pesas cambian su Epg y se mueven, adquieren Ec.
En la foto 5. mientras sostiene las pesas, está aplicando fuerza sobre ellas pero no se produce desplazamiento, no realiza entonces, trabajo mecánico sobre las pesas.
En la foto 6. festeja su logro, la medalla de oro.
1.2. Otros ejemplos
En el caso de un arquero:

Cuando estira la cuerda del arco, el arquero aplica una fuerza y desplaza la cuerda, por tanto realiza una tranferencia de energía por trabajo a la cuerda, como consecuencia ella cambia su Epe.
Para el caso de los deportistas:
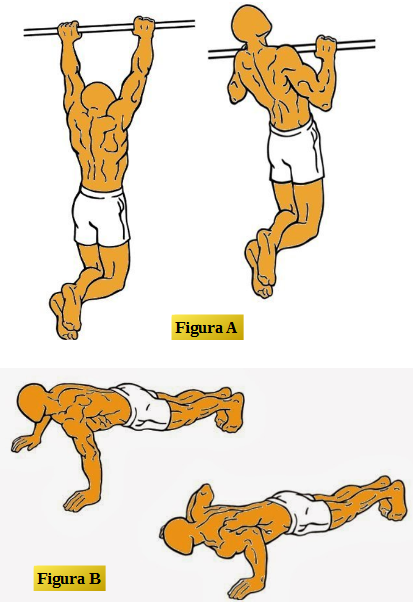
En la figura A la persona efectúa trabajo contra su propio peso, de igual forma en la figura B. La persona realiza fuerza sobre la barra o sobre el piso respectivamente para lograr desplazarse en contra de la fuerza peso que le aplica la Tierra. Por tanto, se realiza trabajo sobre algo cuando se mueve contra la acción de otra fuerza que se opone.
También se puede realizar trabajo para cambiar la rapidez de un objeto, es decir, cuando el objeto experimenta una aceleración.
En el siguiente ejemplo:

El joven empuja el muelle, se cansa al hacerlo, pero el muelle no se mueve, por lo tanto el joven no realiza trabajo sobre el muelle, pues el muelle no cambia su energía.
En todos los casos en los que se efectúa trabajo, se produce una transferencia de energía, un cambio en la energía del cuerpo sobre el que se realiza trabajo.
2. Trabajo realizado por una fuerza constante
La siguiente situación muestra un cuerpo que es arrastrado sobre una superficie horizontal, sometido a la acción de una fuerza ![]() (siendo esta fuerza constante), esta fuerza forma un ángulo α con la dirección del movimiento (Figura 1).
(siendo esta fuerza constante), esta fuerza forma un ángulo α con la dirección del movimiento (Figura 1).
Observar que el cuerpo experimentará un cambio en su velocidad, porque al estar actuando sobre él una fuerza neta está acelerado (por tanto cambiará su Ec).

El cuerpo se desplaza un cierto ![]() , como muestra la figura 2:
, como muestra la figura 2:
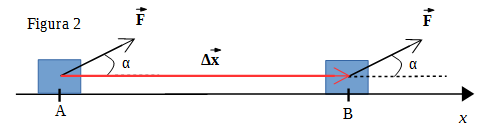

En la ecuación de definición de trabajo,![]() es el módulo del vector fuerza,
es el módulo del vector fuerza,![]() es el módulo del vector desplazamiento, y α es el ángulo formado entre los vectores fuerza y desplazamiento. Para simplificar la notación en la ecuación de trabajo se puede escribir:
es el módulo del vector desplazamiento, y α es el ángulo formado entre los vectores fuerza y desplazamiento. Para simplificar la notación en la ecuación de trabajo se puede escribir:
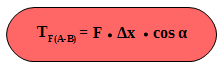
Donde F y Δx representan el módulo de la fuerza y el desplazamiento respectivamente.
Al analizar la ecuación del trabajo se puede deducir su unidad de medida, es el producto entre la fuerza cuya unidad es el N (Newton), el desplazamiento cuya unidad es el m (metro) y el coseno de un ángulo que es una magnitud adimensionada (no tiene unidades). Por tanto, la unidad resultante de dicho producto es: N.m, a esta unidad se le denomina J (Joule) en honor al físico inglés James P. Joule (siglo XIX) quien realizó estudios diversos sobre la energía.
Unidad de trabajo:
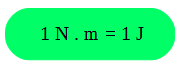
Ejemplo:
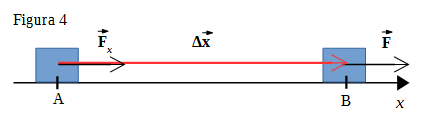
Sobre un cuerpo actúa una fuerza en la dirección de su movimiento como se ve en la Figura 3. Como consecuencia el cuerpo se desplaza la distancia entre los puntos A y B, indicada por el vector desplazamiento ![]() (Figura 4).
(Figura 4).

![]()
El cos 0° = 1, por tanto el trabajo realizado por una fuerza constante que actúa en la dirección del movimiento se determina:
![]()
2.1. Trabajo total o trabajo de la fuerza resultante
Si sobre un sistema (cuerpo de la figura) actúan varias fuerzas:
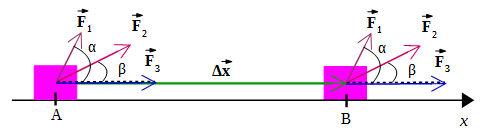
se puede determinar el trabajo total o neto de dos formas:
1) Determinando la fuerza neta y luego calculando el trabajo de la fuerza neta:
![]()
Siendo Fneta el módulo del vector fuerza neta, Δx , el módulo del vector desplazamiento y δ el ángulo entre el vector fuerza neta y el vector desplazamiento.
2) Calculando el trabajo de cada una de las fuerzas y luego sumando los trabajos de cada una:
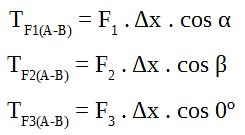
![]()
Ejemplo:
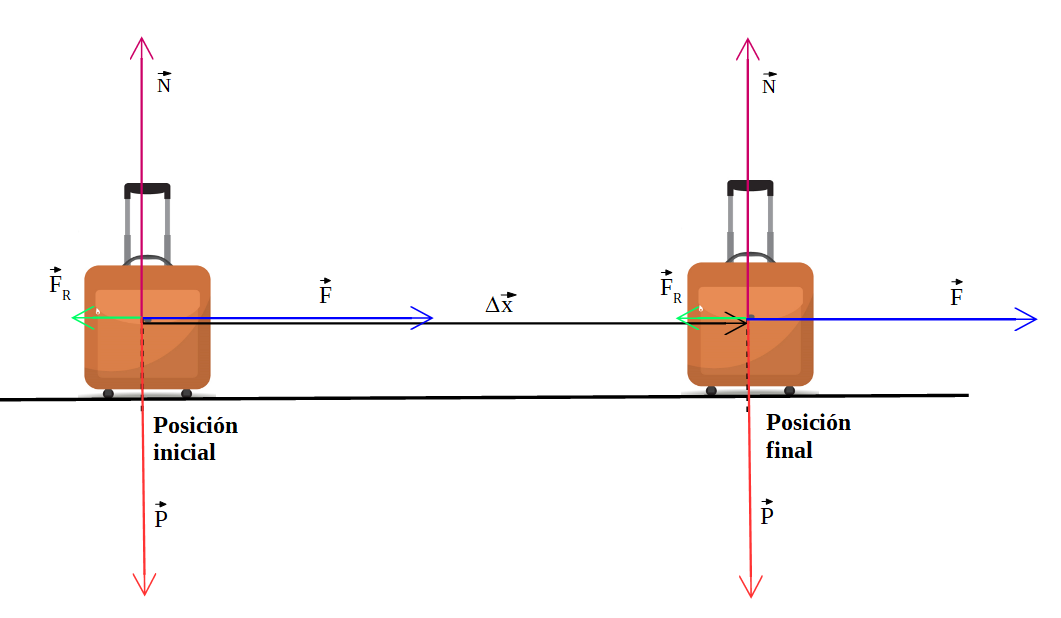
Los valores de las fuerzas son: F = 400 N, Fr = 100 N, P = 400 N, el valor de la normal en este caso es igual al del peso, N = 400 N.
Determinar el trabajo neto realizado sobre la valija, si la misma se desplaza 100 m.
Solución:
Se puede determinar el trabajo de las dos formas descriptas más arriba. En este ejemplo los trabajos realizados por las fuerzas que actúan sobre la valija son calculados siempre entre la posición inicial y la final:
1) Se determina la fuerza neta, para ello se suman las fuerzas las fuerzas en la horizontal, en el eje x
![]()
Al ser colineales y tener sentido opuesto, el módulo de la fuerza resultante en el eje x se determina:
![]()
![]()
A continuación se suman las fuerzas en el eje vertical y:
![]()
la normal y el peso son colineales y de sentido opuesto por tanto:
![]()
![]()
La fuerza neta es la suma de las fuerzas en el eje x y en el eje y, como la suma de fuerzas en el eje y es cero, la resultante es solamente la suma de fuerzas hallada para el eje x:
![]()
![]()
su dirección es horizontal a la derecha:
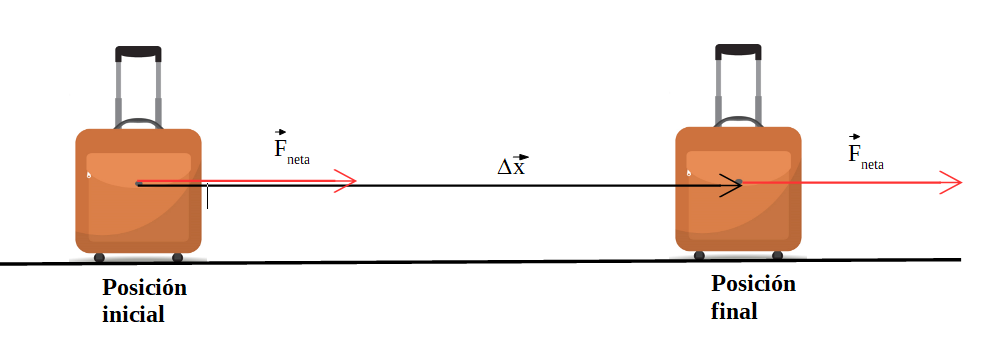
A continuación se determina el trabajo de la fuerza neta entre la posición inicial y final:
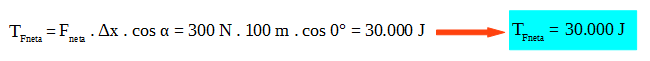
2) En la segunda forma de calcular el trabajo neto, se determina el trabajo de cada una de las fuerzas entre las posiciones inicial y final, y luego se suman:
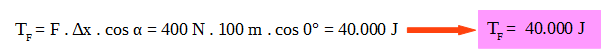
El ángulo α entre la fuerza y el desplazamiento es 0º.
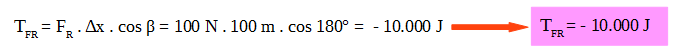
El ángulo entre la fuerza de rozamiento y el desplazamiento es 180º.

El ángulo δ entre la fuerza normal y el desplazamiento es 90º.

El ángulo θ entre la fuerza peso y el desplazamiento es 90º.
El trabajo neto es entonces la suma de los trabajos de cada una de las fuerzas que actúan sobre la valija (entre las posiciones inicial y final):
![]()
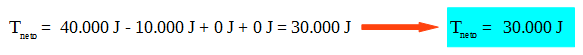
Se puede observar que el trabajo calculado por las dos formas da lo mismo.
2.2. Ejemplos
1) Sobre un cuerpo actúa una fuerza de módulo 20 N como se ve en la figura, el cuerpo se desplaza una distancia de 10 m.
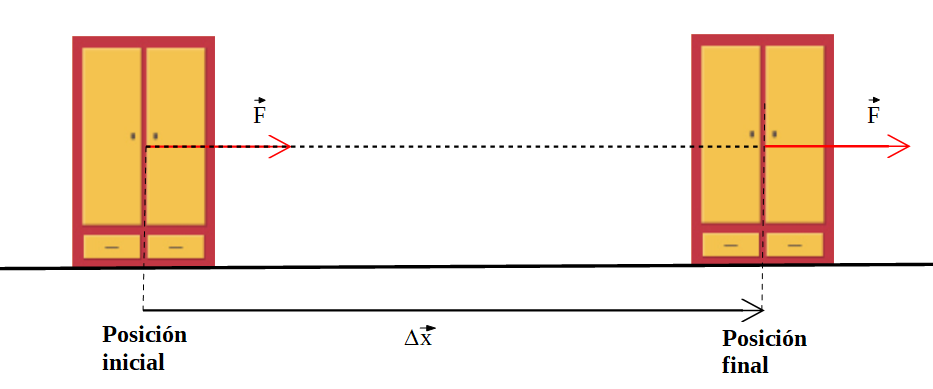
Nota: Se representa más abajo el vector desplazamiento, sólo para visualizarlo con más claridad.
Determinar el trabajo realizado por la fuerza ![]() entre la posición inicial y la final, indicadas.
entre la posición inicial y la final, indicadas.
Solución:
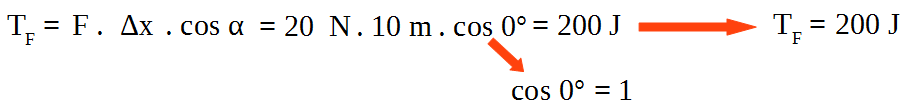
2) Sobre la caja de la figura está representada la fuerza normal a la superficie, su valor es de 30 N, el cuerpo se desplazó desde una posición inicial a la posición final, también está indicado el vector desplazamiento, su valor es de 2,0 m. Observar que el ángulo entre la fuerza normal y el vector desplazamiento es de 90°.
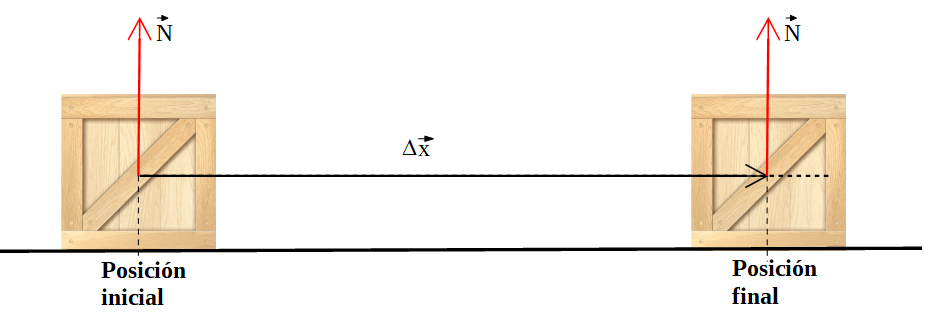
Determinar el trabajo realizado por la fuerza normal, entre la posición inicial y final indicadas.
Solución:
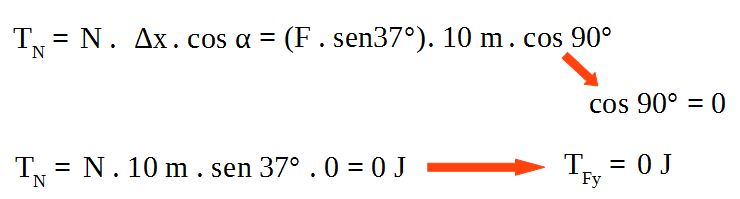
Conclusión: cualquier fuerza que tenga dirección perpendicular al desplazamiento, no realiza trabajo mecánico.
3) Sobre un baúl actúa una fuerza de módulo 20 N como se ve en la figura, el baúl se desplaza una distancia de 10 m.
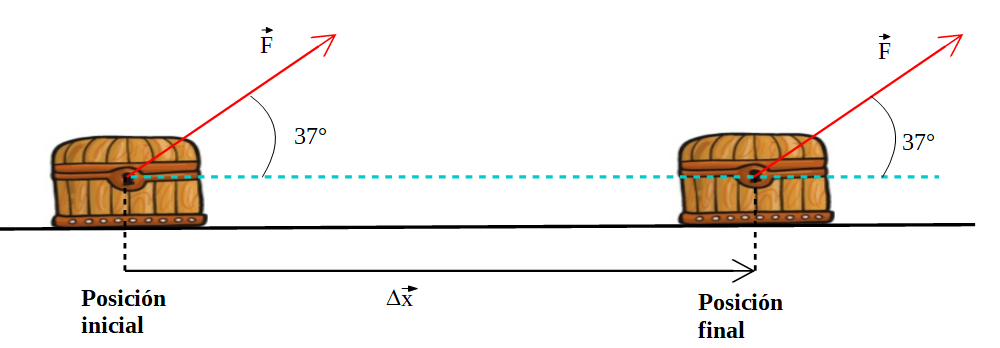
Determinar el trabajo realizado por la fuerza ![]() entre la posición inicial y final indicadas.
entre la posición inicial y final indicadas.
Solución:
![]()
En este último ejemplo se descompone la fuerza ![]() , para determinar el trabajo de cada una de las componentes de la fuerza y luego calcular el trabajo total sumándolos, TF = TFx + TFy:
, para determinar el trabajo de cada una de las componentes de la fuerza y luego calcular el trabajo total sumándolos, TF = TFx + TFy:
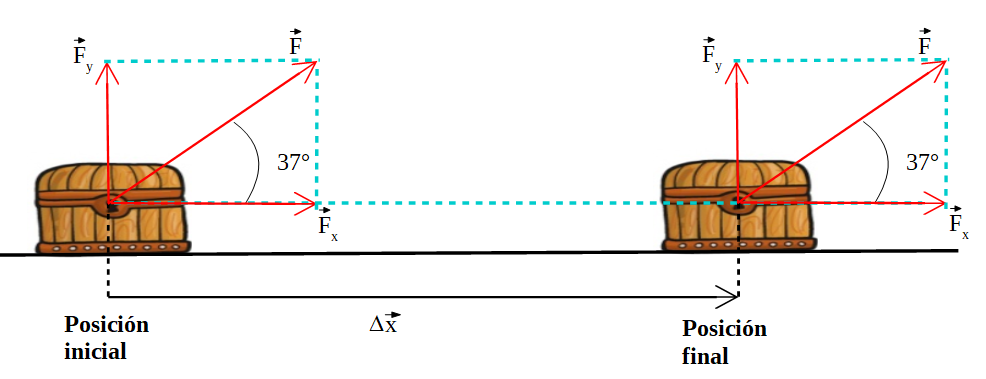
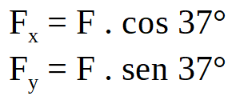
El trabajo total o trabajo neto realizado sobre un cuerpo, se determina sumando los trabajos de cada una de las fuerzas que actúan sobre el cuerpo. Por tanto al descomponer la fuerza ![]() tomamos el trabajo realizado por ella como la suma de los trabajos realizados por cada componente:
tomamos el trabajo realizado por ella como la suma de los trabajos realizados por cada componente:
![]()
El trabajo de la componente de ![]() en el eje x:
en el eje x:
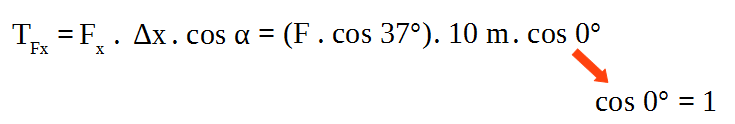
Al reordenar la expresión:

Se observa que esta expresión es igual a la usada para calcular el trabajo de ![]() , sin la descomposición de la fuerza:
, sin la descomposición de la fuerza:
![]()
El trabajo de la componende de ![]() en el eje y:
en el eje y:
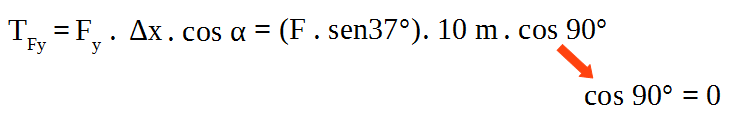
![]()
La suma de ambos trabajos:
![]()
La componente de la fuerza ![]() que realiza trabajo es solamente la que tiene igual dirección que el desplazamiento, en este caso es la componente x de
que realiza trabajo es solamente la que tiene igual dirección que el desplazamiento, en este caso es la componente x de ![]() . La componente que es perpendicular con respecto al desplazamiento no realiza trabajo, en este caso es la componente vertical, y.
. La componente que es perpendicular con respecto al desplazamiento no realiza trabajo, en este caso es la componente vertical, y.
3. Relación entre el trabajo y la energía cinética
Sobre una caja que se encuentra en la posición inicial y se mueve con una velocidad inicial (cuyo valor es vi), se aplica una fuerza (Fneta porque es la resultante de todas las fuerzas aplicadas sobre la caja), como muestra la figura, como consecuencia la velocidad de la caja aumenta porque ésta se acelera.
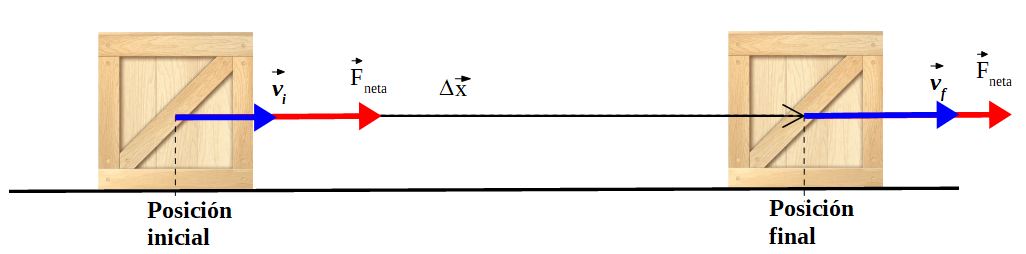
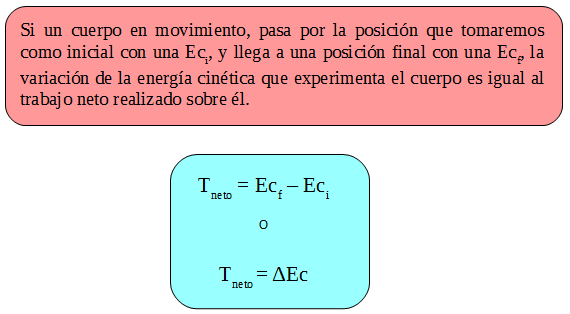
Esta fuerza realiza trabajo sobre la caja, le transfiere energía, la caja que inicialmente se encontraba moviéndose con una velocidad, es decir posee una Eci, aumenta su energía cinética, pues aumenta su velocidad, Ecf. Toda la energía transferida por el trabajo realizado por la fuerza se transforma en energía cinética, por tanto:
TFneta = ΔEc = Ecf - Eci
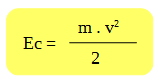
Resumiendo:
4. Relación entre el trabajo y la energía potencial
La energía potencial está asociada a la posición relativa de las partículas en función de las interacciones fundamentales. Se analizan aquí los casos cuando la fuerza peso o la fuerza elástica realizan trabajo sobre un cuerpo y su relación con la energía potencial vinculada a esta transferencia.
* Relación entre el trabajo del peso y la energía potencial gravitatoria
La pelota de la figura se desplaza de la posición inicial a la final por la acción de la fuerza peso representada:
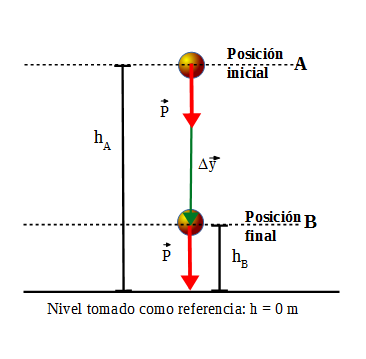
El trabajo realizado por la fuerza peso: puede ser que actúen otras fuerzas sobre la pelota, pero aquí sólo se focalizará en el trabajo que realiza la fuerza el peso. Por lo que el trabajo realizado por la fuerza peso desde A a B es:
TP(A-B) = P . Δy . cos 0º
El módulo del desplazamiento de la pelota es Δy = hA - hB, y el módulo del peso P = m . g y cos 0º = 1
TP(A-B) = m . g . (hA - hB)
Por otro lado si analizamos las Epg inicial y final, vemos que inicialmente la pelota tiene una EpgA = m . g . hA. En la posición final su EpgB = m . g . hB. Por lo que su variación de Epg es:
ΔEpg = EpgB - EpgA
ΔEpg = m . g . hB - m . g . hA
ΔEpg = m . g . (hB - hA)
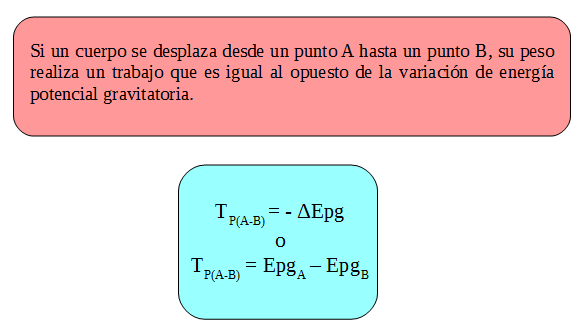
Al comparar: TP(A-B) = m . g . (hA - hB) con ΔEpg = m . g . (hB - hA) se observa que si a ΔEpg multiplicamos por -1 obtenemos TP(A-B).
ΔEpg = m . g . (hB - hA) - ΔEpg = - m . g . (hB - hA)
- ΔEpg = m . g . (hA - hB) esta última expresión es igual a TP(A-B) = m . g . (hA - hB)
En conclusión:
* Relación entre el trabajo de la fuerza elástica y la energía potencial elástica
De forma análoga a cómo se estudió la relación entre el trabajo del peso y la energía potencial gravitatoria se puede deducir que la relación entre el trabajo realizado por la fuerza elástica y la energía potencial elástica es:

* El trabajo también se relaciona con otras energías potenciales que no estudiaremos en este módulo.
5. Potencia
La potencia es el trabajo efectuado sobre un cuerpo por unidad de tiempo. Es decir, es la energía transferida de un cuerpo a otro por unidad de tiempo. La potencia es la medida de cuán rápido se hace trabajo.
Al subir una montaña cargando un cajón con manzanas, se realiza el mismo trabajo si se sube caminando que si se sube corriendo. Sin embargo, el cansancio es mayor al subir la montaña corriendo con la carga.
En el caso de los motores es importante saber la potencia, pues es el trabajo que puede efectuar el motor por unidad de tiempo, es decir, es la rapidez con la que realiza el trabajo o la rapidez con la que se produce la transferencia de energía.

La unidad de medida de la potencia es:
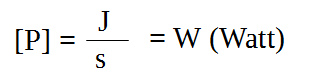
Es muy común que se utilicen múltiplos de esta unidad: kW (kilo Watt, 1.000 W) o MW (mega Watt, 1.000.000 W).
Otra unidad frecuente para la potencia de los motores de combustión es el caballo de fuerza, el símbolo de esta unidad es hp, por sus iniciales en inglés horse power, la equivalencia entre hp y W es:
![]()
6. Créditos
Bibliografía consultada:
- Hewitt, P. (2007). Física conceptual. México: Pearson-Addison Weasley.
- Alvarenga, B., Máximo, A. (1997). Física general. México: Oxford University.
- Laboratorio de Fisicoquímica IINN. (2012). Energía - una visión del problema. Montevideo.
Las imágenes utilizadas fueron tomadas de:
- Ejemplo: Capturas de pantalla del siguiente vídeo: Gold for retiring 62kg
Colombian weightlifter. Autor: Olympics. Licencia estándar de You Tube.
Recuperado de: https://www.youtube.com/watch?v=QVkkxA7AMHY
- Otros ejemplos: Bardo el arquero. Autor: Fandom. Licencia: CC BY-SA
- Otros ejemplos: Imágenes de musculación. Autor: Gottau, G. Licencia: CC BY-NC 3.0.
- Otros ejemplos: Joven haciendo push ups cerca del mar. Autor: Nensuria - Freepik.com. Licencia: CC BY 3.0.
- Trabajo total o trabajo de la fuerza resultante: Variedad de bolsos. Autor: Freepik. Licencia: CC BY 3.0.
- Ejemplos: 30 interior and funiture icons. Autor: Graphiqa Stock/Freepik. Licencia: CC BY 3.0.
- Ejemplos: Lindos objetos para videojuegos dibujados a mano: Autor: Freepik. Licencia: CC BY 3.0.
- Ejemplos: Ícono cajón de madera. Autor: Psd Graphics. Licencia: CC BY 3.0.
- Relación entre trabajo y energía potencial: Pelota en dos posiciones diferentes. Autor: Pedreira, S. Licencia: CC BY 4.0
Autoría del Módulo: Profesora Silvia Pedreira.
spedreira@uruguayeduca.edu.uy
Esta obra está bajo una Licencia Creative Commons Atribución 4.0 Internacional.
Portal Uruguay Educa.
Agosto de 2017. Actualizado en Marzo de 2020.