Algunas resoluciones
Libro que contiene parte de las resoluciones de problemas planteados.
| Sitio: | Aulas | Uruguay Educa |
| Curso: | Matemática - 2º C.B. |
| Libro: | Algunas resoluciones |
| Imprimido por: | Invitado |
| Día: | jueves, 3 de abril de 2025, 23:59 |
1. Problemas


En este libro tendrás las resoluciones de los problemas, presentando algunas estrategias, pero recuerda que siempre es posible resolverlos de otra forma.
¡Trata de hacerlos tú solo o con un compañero!
A la izquierda de tu pantalla encontrarás la tabla de contenidos para acceder a la lista de los problemas resueltos (o planteados).

¡Éxitos!
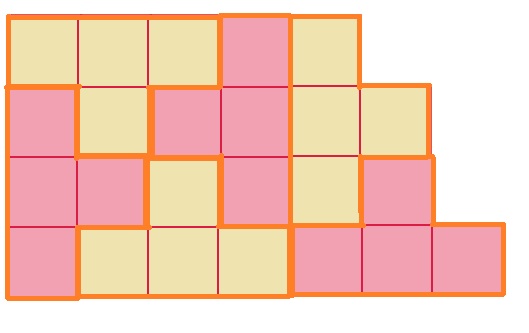
2. Dividir la figura
Una estrategia es contar cuántos cuadraditos la componen.
Como son 24 y tiene que ser dividida en 6 figuras iguales, sabemos entonces que hay que dividirla en figuras de 4 cuadraditos.
3. Torre de cubos
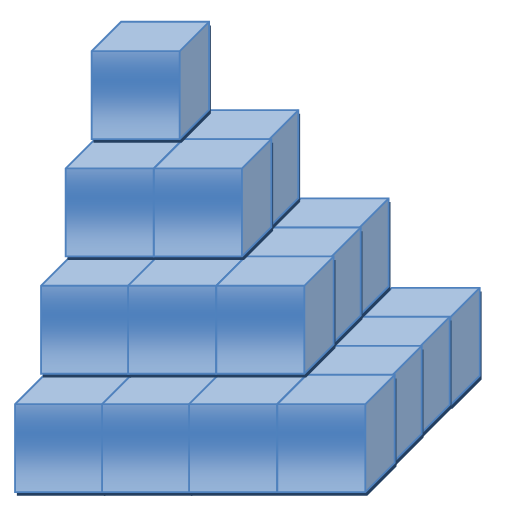
Una estrategia es pensar en cada piso.
El de abajo es un cuadrado de 4 cubitos de lado. Por lo tanto tiene 16 cubitos.
El primer piso tiene 3 cubitos de lado, por lo tanto tiene 9 cubitos, etc.
16+9+4+1=30
Se construye con 30 cubitos.
4. Perímetro y área

Se sabe que esta figura está compuesta por 3 cuadrados iguales, y que su perímetro es 24 cm.
Una estrategia sería dividir la figura en cuadrados de lado u y plantear la medida de cada lado de la figura.
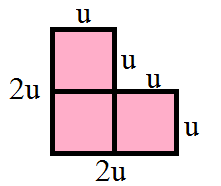
Planteamos el perímetro: P=2u+2u+u+u+u+u=8u
Como el perímetro es 24, entonces: 8u=24, por lo tanto u= 3.
Entonces el área de cada cuadradito es 9.
El área de la figura es 27cm2
Otra estrategia puede ser formar un cuadrado grande:
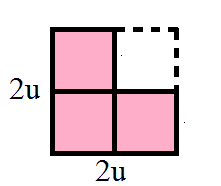
Este cuadrado también tiene perímetro 24, y es más fácil ver que cada cuadradito tiene 3cm de lado, ya ue 6x4=24.
5. Ampliar la figura
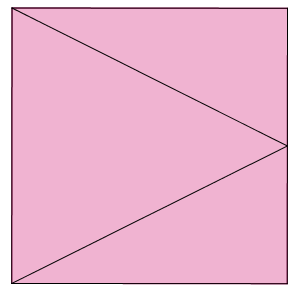
Una estrategia es pensar en las dimensiones del cuadrado.
Si su lado es u, al ampliarlo tendrá lado 2u.
La figura original tiene área u2, mientras que la ampliada tendrá área 4u2. Se cuatriplicó el area, no se duplicó.
Otra estrategia puede ser dar un valor concreto al lado, por ejemplo 1.
Piénsalo para el triángulo.
6. Triángulo en circunferencia
Si construimos los triángulos según las condiciones encontramos sólo 2 puntos R y R', ya que la única opción es que el ángulo recto esté en O.
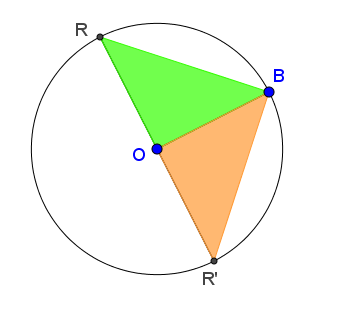
Y ambos triángulos OBR y OBR' son isósceles porque OR y OB son radios de la corcunferencia, por lo tanto son iguales.
7. Cuadrado en cuadrado
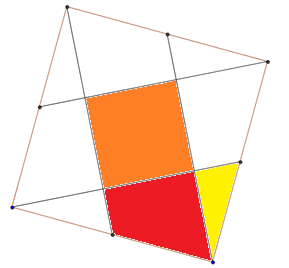
Una estrategia para este problema es observar cómo está dividido el cuadrado.
Si nos fijamos en trapecio rojo y el triángulo amarillo podemos probar que la suma de sus áreas es igual al área del cuadrado naranja.
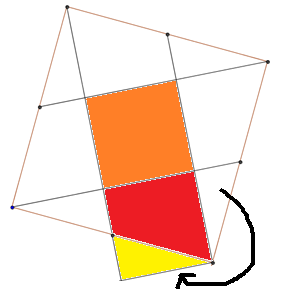
8. Cubo pintado
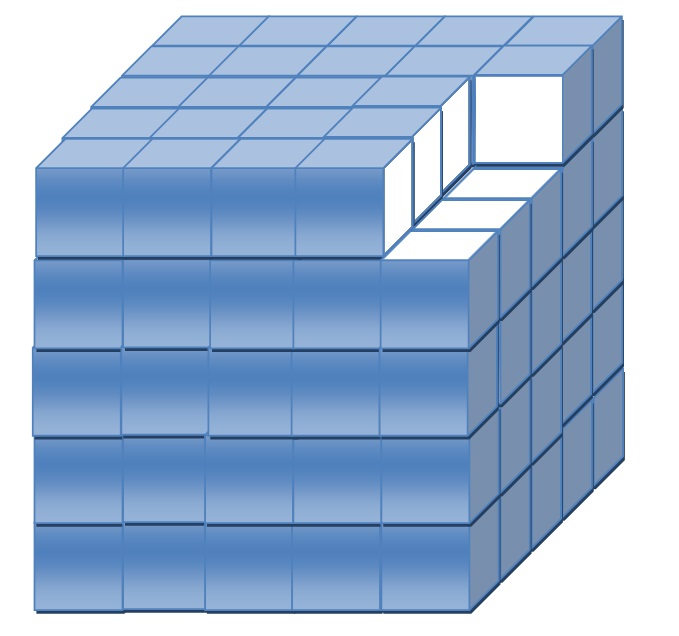
Una estrategia es primero contar cuántos cubitos forman el cubo grande.
Como tiene 5 cubitos de lado, entonces está formado por 125 cubitos.
De ellos están pintados sólo los que están "por fuera"
Por eso piensa en los que están en las esquinas, en las aristas y en las caras del cubo grande, de esta forma podrás ver cuántos cubitos quedaron pintados.
Respuestas:
No
8
36
54
64
9. ¿Cuántos metros de tejido?
Este problema es similar a "Perímetro y área"
Por lo tanto solo plantearemos la solución, (para que corrobores),
¡Lo importante es que lo pienses!
Solución: 120 metros.
10. Compara triángulos
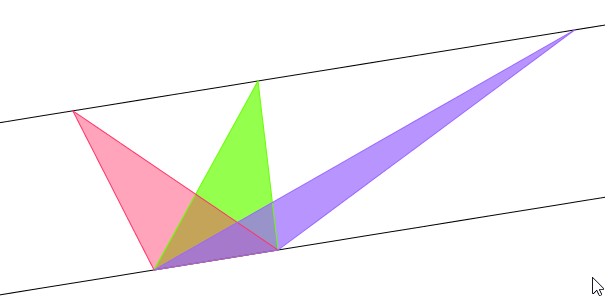
En este problema una estrategia es fijarnos en las características de los tres triángulos.
Los tres comparten un lado, y como los vértices opuestos a ese lado pertenecen a una recta paralela a la recta que contiene el lado, podemos decir que la altura de los tres triángulos es igual. Por eso tienen los tres la misma área.