Instrumentos y medidas
| Sitio: | Aulas | Uruguay Educa |
| Curso: | Ciencias Físicas - 1º C.B. |
| Libro: | Instrumentos y medidas |
| Imprimido por: | Invitado |
| Día: | jueves, 3 de abril de 2025, 02:13 |
Tabla de contenidos
1. Instrumentos y medidas
En este módulo definiremos conceptos básicos de las ciencias experimentales. Con toda seguridad en cualquier investigación por más simple que sea, tendremos que realizar alguna medida. Cuando deseamos medir, necesitamos elegir un instrumento adecuado, realizaremos con él la medida y la registraremos.
Es importante antes de comenzar ponernos de acuerdo en algunos conceptos:
Magnitud: una magnitud es una propiedad de los cuerpos que puede ser medida, para realizar la medida se usa un patrón de referencia que define a la magnitud. El instrumento de medida de una magnitud es fundamental para poder definirla. Son ejemplos de magnitudes, la masa, el tiempo, etc.
Medir: realizar una medida es comparar lo que queremos medir con una cantidad conocida de la misma magnitud y que tomamos como unidad. Cuando logramos medir una determinada magnitud, tendremos un número con su correspondiente unidad de medida.
Por ejemplo, cuando vas al control médico se toman medidas de tu talla, masa corporal, a veces temperatura, etc.
- Para medir tu talla (longitud del cuerpo desde los pies a la cabeza) se utiliza un metro que es un instrumento cuya medida está calibrada según acuerdos internacionales, por ejemplo 1,5 m (metros).
- De igual modo para medir tu masa se utiliza la balanza, por ejemplo 50 kg (kilogramos), y para medir tu temperatura se utiliza un termómetro, 36,5 °C.
En Estados Unidos y el Reino Unido, utilizan un sistema de unidades diferente al nuestro, por ejemplo para medir longitudes utilizan la unidad llamada pie y para medir la masa utilizan la libra, si tu vas al control médico y te dicen que tu talla es 49,2 pies y tu masa es 110,2 libras, no vas a tener mucha idea de qué cantidades representan ya que no son unidades de uso cotidiano para nosotros. Por eso es muy importante la definición de los patrones de medida, es decir los objetos de referencia con los que comparamos lo que deseamos medir.
2. Magnitudes y sus unidades
El Sistema Métrico Decimal fue aprobado por el gobierno francés en 1795, luego en 1875 fue ratificado por los países más importantes del mundo, de esta forma este sistema tomó un alcance internacional.
La Conferencia General de Pesas y Medidas en su versión número 14, en el año 1960 con el acuerdo de 36 países aprobó el Sistema Internacional de Unidades, que se abrevia S.I. Nuestro país forma parte de ese acuerdo internacional donde se establecen las unidades para cada magnitud.
En la siguiente tabla se muestran algunas magnitudes y sus unidades:
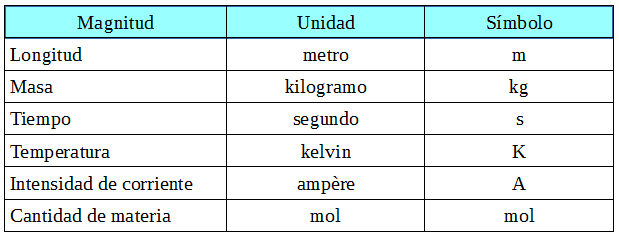
En algunas medidas es útil el uso de múltiplos o submúltiplos de estas unidades:
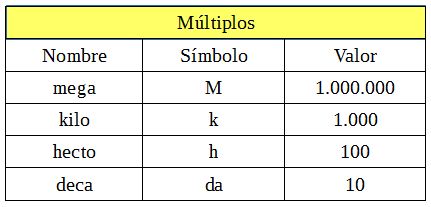

Ejemplos:
1 km son 1000 m
1 cm son 0,01 m
3. Instrumentos de medida
Para medir las diferentes magnitudes se utilizan instrumentos que permiten hacerlo, las siguientes imágenes son ejemplos:
Medida de longitudes:
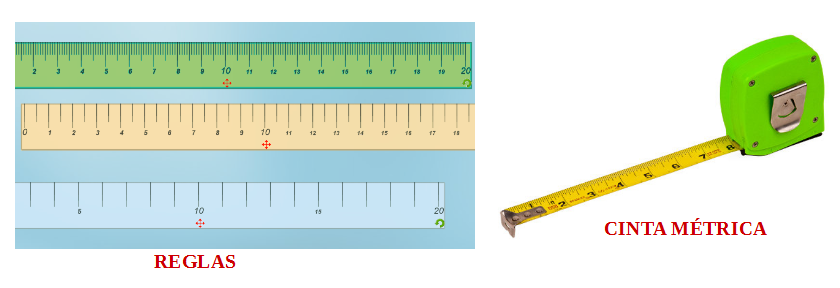
Medida de masas:

Medida del tiempo

Medida de temperatura

Medida de volumen:

Cuando deseamos realizar una medida, debemos elegir el instrumento que sea adecuado, para ello debemos tener en cuenta dos características fundamentales que son el alcance y la apreciación.
3.1. Alcance de un instrumento de medida
El alcance es la mayor medida que se puede registrar con un instrumento.
Ejemplos:
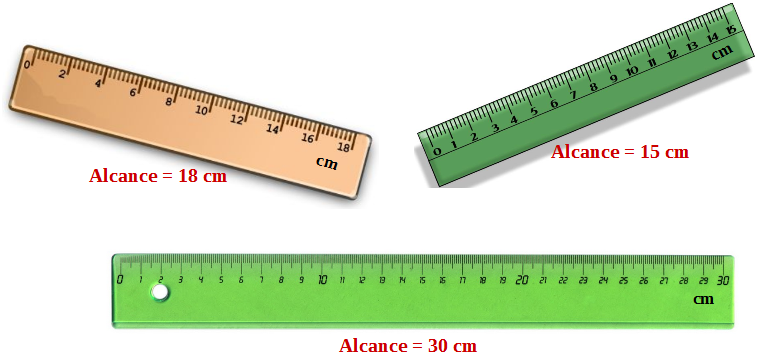


3.2. Apreciación de un instrumento de medida
La apreciación es la menor variación de la medida que se puede registrar con un instrumento.
En aquellos instrumentos que tienen una escala, el valor entre dos divisiones consecutivas es la apreciación. En los instrumentos digitales la apreciación es el menor cambio que se registra en él.
Ejemplos:
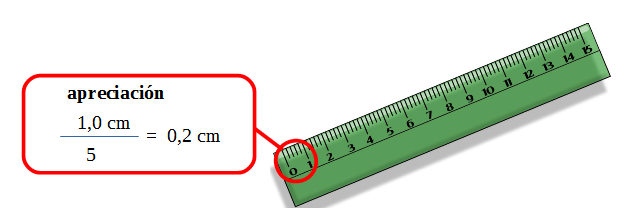
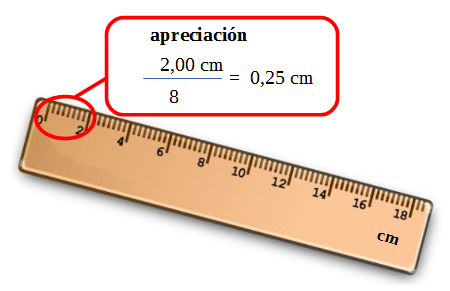
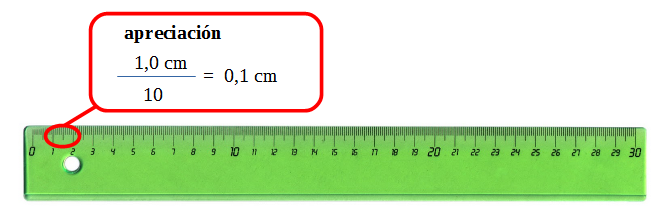
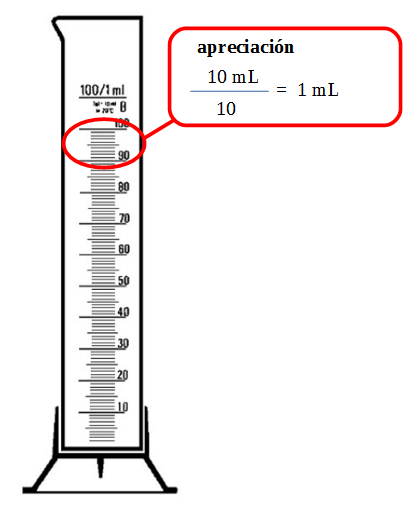


En el caso de un instrumento digital la apreciación es lo mínimo que puede variar el último dígito que se muestra en la pantalla, en el caso de la balanza anterior es 0,01 g.
3.3. Estimación de una medida
La estimación es un proceso que realiza el observador, dónde éste evalúa qué fracción de la apreciación del instrumento le corresponde a una medida.
Si la medida queda entre dos divisiones, como en el caso de la siguiente imagen:

El termómetro de la figura tiene una apreciación de 1 °C, la lectura de la temperatura en este ejemplo queda entre la división 97 y 98 °C. El observador para realizar esta medida debe tomar la decisión en cuántas partes puede dividir el intervalo, eso va a depender de la destreza que tenga. En este caso la medida queda en la mitad del intervalo, siendo la lectura: 97,5 °C.
Este proceso por el cual la persona que realiza la medida, dividiendo a "ojo" el intervalo graduado se denomina estimar la medida. De esta forma podemos decir que todas las medidas tienen un margen de incertidumbre, ya que va a depender del instrumento y del observador.
El margen de incertidumbre de una medida "M" se expresa como "δM", en el ejemplo de la medida de la temperatura: (t ± δt) °C.
t = (97,5 ± 0,5) ºC
Esto quiere decir que la medida se encuentra en el intervalo entre
- 97,5 ºC - 0,5 ºC = 97,0 ºC y
- 97,5 ºC + 0,5 ºC = 98,0 ºC.
Todas las medidas tienen un margen de incertidumbre, ya sea que estimemos o no la misma.
La incertidumbre o error de una medida, δM, coincide generalmente con la estimación de la medida o a veces con la apreciación del instrumento. Por tanto, siempre que realicemos una medición debemos informar la incertidumbre de la misma.
4. Cifras significativas
En la medida de temperatura del ejemplo del capítulo anterior:
t = (97,5 ± 0,5) ºC
Este valor 97,5 ºC, está compuesto por 3 cifras (un 9, un 7 y un 5) de estas 3 cifras el 5 no es seguro pues está afectado por la incertidumbre de la medida. Las otras dos cifras el 9 y el 7 son cifras seguras, ellas no están afectadas por la incertidumbre.
En una medida, las cifras significativas son todas las cifras seguras y una única cifra insegura, que corresponde al último dígito de la medida. Cuando realizamos una medida, la debemos expresar utilizando sólo las cifras significativas.
En los siguientes ejemplos explicitaremos algunas reglas:
* 0,0037 kg, en este caso hay 2 cifras significativas el 3 y el 7, los ceros que indican el lugar decimal, es decir los ceros a la izquierda del primer número diferente de cero no son cifras significativas.
* 30,2 L, aquí son 3 cifras significativas, el 3 el 0 y el 2. Los ceros que quedan entre dos cifras significativas son significativos.
* 7,100 m, en este último ejemplo son 4 cifras significativas. Los ceros a la derecha del último número diferente de cero son significativos.
Si comparamos dos medidas: 31 cm y 31,0 cm, parecería que no hay diferencia, pero sí la hay. Las cifras significativas de 31 cm son dos, significa que tiene una cifra segura (el 3) y una cifra insegura (el 1). El 31,0 cm, tiene tres cifras significativas, dos cifras seguras (el 31) y una cifra insegura (el 0).

En este ejemplo hemos tomado como incertidumbre la apreciación del instrumento. Esto significa que la medida 31,0 cm es más precisa que la 31 cm, en esta última el margen de incertidumbre es mayor.
4.2. Cifras significativas y las operaciones matemáticas
Cuando se realizan operaciones con las medidas de un experimento, es importante respetar el número de cifras significativas del resultado. Las cifras significativas están relacionadas con la "precisión" de las medidas, por lo que no es posible que los resultados de las operaciones tengan mayor precisión que las medidas originales.
Suma y resta
Hemos comprado en un supermercado 1,0 kg de queso, luego en el almacén de la esquina compramos 540 g más. Para determinar la masa total de queso debemos sumar las masas.
El valor 1,00 kg que posee 3 cifras significativas y dos cifras después de la coma, de las que la última es la cifra insegura. Indicaremos la cifra insegura: ![]()
El valor 540 g, 3 cifras significativas, este valor tiene una unidad diferente del primer valor, por tanto lo convertiremos a kg, de ese modo los podremos sumar: 0,543 kg, el valor continúa teniendo 3 cifras significativas y tres cifras después de la coma, de las cuales la última el 3 es la cifra insegura: ![]()
Al realizar la suma:
![]()
Expresada de otra forma:
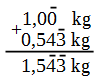
La suma tiene dos cifras seguras y dos inseguras, la expresión del resultado se debe realizar con todas las cifras seguras y la primera insegura, para ello debemos redondearlo, así que como el "3" es menor que cinco, el valor queda en 1,54 kg.
El resultado de sumar o restar dos medidas debe tener el mismo número de cifras decimales (lugares después de la coma) que el número que tenga menos.
Reglas de redondeo: en el siguiente enlace de Wikipedia puedes estudiar y ver ejemplos sobre el redondeo de las medidas.
Producto y división
Deseamos calcular el área de un piso para ir a comprar la cerámica: para hacer la medida usamos un metro y registramos 3,7 m de largo y 1,45 m de ancho.
Al calcular el área:
![]()
Los datos de las medidas, tienen dos y tres cifras significativas, el resultado del producto se debe expresar con igual cantidad de cifras significativas como el valor que tiene menor cantidad de cifras significativas, en este caso dos. Por tanto el resultado final será 5,4 m2. Tal como lo estudiaste en el enlace de Wikipedia, para redondear 5,365 a dos cifras, nos tenemos que quedar con el 5 y con el 3 pero como el número que le sigue al 3 es un 6 debemos sumar un dígito al 3, por lo que el resultado expresado con dos cifras queda 5,4 m2
El resultado de una multiplicación o división tendrá igual cantidad de cifras significativas como el factor que tenga menos cifras significativas.
4.3. Video explicativo - Cifras, operaciones y redondeo
Mira con atención el siguiente video, ten en cuenta que en una parte del mismo habla de cómputos que significa operaciones matemáticas.
5. Notación Científica
Mira el siguiente video explicativo sobre cómo se hace para escribir un número en notación científica.
Esto es útil pues cuando deseamos redondear un número con determinada cantidad de cifras significativas, a veces no hay otra forma de hacerlo si no es con la notación científica.
6. Créditos
Bibliografía consultada/Sitios:
- Segurola, B; Saravia, G; Szwarcfiter, M. (1996). Ciencias Físicas 1. Montevideo, Uruguay: Textos del Sur.
- Hewitt, P. (2007). Física Conceptual. México: Addison Wesley Longman.
- Alvarenga, B., Máximo, A. (1997). Física general. México: Oxford University
- Redondeo. https://es.wikipedia.org/wiki/Redondeo
Imágenes:
- Instrumentos y medidas: http://recursostic.es/multidisciplinar/wikididactica/images/Reglasgraduadas.png
- Instrumentos y medidas: http://www.educando.edu.do/files/7813/3070/8925/cinta_metrica.jpg
- Instrumentos y medidas: https://spanish.alibaba.com/product-detail-img/solo-pan-balanza-de-desigual-de-brazo-con-3-vigas-triple-haz-balanza-475842784.html
- Instrumentos y medidas: http://www.kalkumezquerra.com/images/metrologia/cronometros_digitales_2_funciones_.jpg
- Instrumentos y medidas: http://www.confianzamarketing.com/productos/Reloj/relojdearena.jpeg
- Instrumentos y medidas: http://www.marienfeld-superior.com/system/html/63.901.00-e430dd7f.jpg
- Instrumentos y medidas: https://janomedical.com/shop/wp-content/uploads/2015/11/termohigrometro-humedad-temperatura-analogo-farmacias-533001-MEC20263461446_032015-O.jpg
- Instrumentos y medidas: http://media.rs-online.com/t_large/F2068856-01.jpg / http://soñar-con.com/wp-content/uploads/2016/04/So%C3%B1ar-con-term%C3%B3metro.jpg
- Instrumentos y medidas: http://www.auxilab.es/controles/ObtenerImagen.ashx?f=%5c00%5c00%5c4f%5c05_DBB001_9.jpg
- Instrumentos y medidas: http://www.museohistoricodeenfermeria.org/panel/output/files/CEA_0227%20r%20ok.jpg
- Instrumentos y medidas: http://img.directindustry.es/images_di/photo-mg/28307-7552157.jpg
- Alcance de un instrumento de medida: http://t2.gstatic.com/images?q=tbn:ANd9GcQGuGqozwTHcd_Ls79O4PtMLoOHXEdqEZfxfBQMIAjP-hZsIg4reZd_xQ
- Alcance de un instrumento de medida: https://s-media-cache-ak0.pinimg.com/236x/bd/1f/ef/bd1fef609f5cd5dd8f5609e29008a743.jpg
- Alcance de un instrumento de medida: http://img.directindustry.es/images_di/photo-g/54946-3949091.jpg
- Alcance de un instrumento de medida: https://spanish.alibaba.com/product-detail-img/solo-pan-balanza-de-desigual-de-brazo-con-3-vigas-triple-haz-balanza-475842784.html
- Apreciación de un instrumento de medida: http://t2.gstatic.com/images?q=tbn:ANd9GcQGuGqozwTHcd_Ls79O4PtMLoOHXEdqEZfxfBQMIAjP-hZsIg4reZd_xQ
- Apreciación de un instrumento de medida: https://s-media-cache-ak0.pinimg.com/236x/bd/1f/ef/bd1fef609f5cd5dd8f5609e29008a743.jpg
- Apreciación de un instrumento de medida: http://img.directindustry.es/images_di/photo-g/54946-3949091.jpg
- Apreciación de un instrumento de medida: https://spanish.alibaba.com/product-detail-img/solo-pan-balanza-de-desigual-de-brazo-con-3-vigas-triple-haz-balanza-475842784.html
- Apreciación de un instrumento de medida: http://www.boeco.com/system/SiteLoad.php?Foto=180.jpg&keepThis=true&
- Estimación de una medida: https://apuntomania.files.wordpress.com/2012/06/fig3.png
Vídeos:
- Cifras significativas. Jorge Cogollo. https://www.youtube.com/watch?v=Ina-E8NEF6U
- Cifras significativas, operaciones y redondeo. J. Córdova. https://www.youtube.com/watch?v=nZLlbs44yaw&t=25s
- Notación científica. Laracos Math. https://www.youtube.com/watch?v=EMYTxbpXnJI
Autoría del Módulo: Profesores Anarella Gatto, Sebastián Mendieta y Silvia Pedreira.
agatto@uruguayeduca.edu.uy
spedreira@uruguayeduca.edu.uy
Esta obra está bajo una Licencia Creative Commons Atribución 4.0 Internacional.
Portal Uruguay Educa.
Junio de 2017.