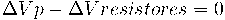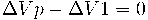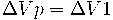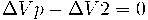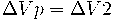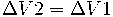Magnitudes eléctricas y circuitos
| Sitio: | Aulas | Uruguay Educa |
| Curso: | Física - 1º B.D. |
| Libro: | Magnitudes eléctricas y circuitos |
| Imprimido por: | Invitado |
| Día: | jueves, 3 de abril de 2025, 17:17 |
Tabla de contenidos
- 1. Introducción
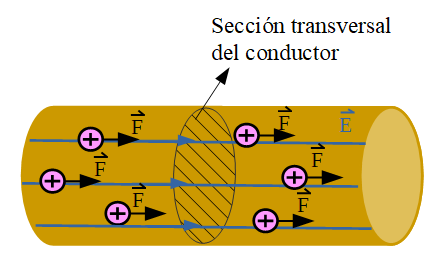
- 2. Corriente eléctrica
- 3. Intensidad de corriente
- 4. Energía potencial eléctrica
- 5. ¿Qué es la diferencia de potencial o voltaje?
- 6. Circuito eléctrico
- 7. ¿Cómo se mide la intensidad de corriente en un circuito eléctrico?
- 8. ¿Cómo se mide la diferencia de potencial entre dos puntos de un circuito eléctrico?
- 9. Resistencia eléctrica
- 10. Potencia eléctrica
- 11. Créditos
1. Introducción
El siguiente video introduce varios de los conceptos que se trabajarán en el módulo. Visualízalo con atención y luego recorre el resto de los capítulos.
2. Corriente eléctrica
En el siguiente recurso debes hacer clic en los diferentes elementos interactivos y toma nota de los temas tratados.3. Intensidad de corriente
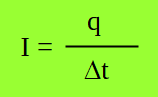

3.1. Ejemplo
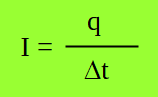
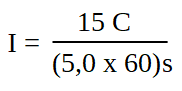
4. Energía potencial eléctrica
Cuando una fuerza desplaza un cuerpo y ella está siendo aplicada en la dirección del movimiento, sobre el cuerpo se está realizando un trabajo. Este trabajo realizado sobre el cuerpo está relacionado con la energía potencial. La energía potencial está relacionada con la posición del cuerpo dentro de un cierto campo.
Si un cuerpo se eleva una cierta altura, se realiza sobre él un trabajo y aumenta su energía potencial gravitatoria. A medida que aumenta la altura, mayor será su energía potencial gravitatoria con respecto a la altura de referencia.
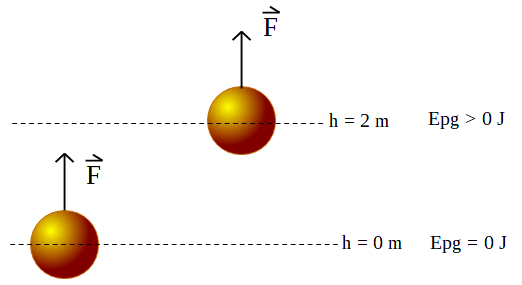
Figura 2. Cuerpo que es desplazado mediante una fuerza dentro del campo gravitatorio terrestre.
La energía potencial de un cuerpo cargado va a estar vinculada a su posición dentro de un campo eléctrico.
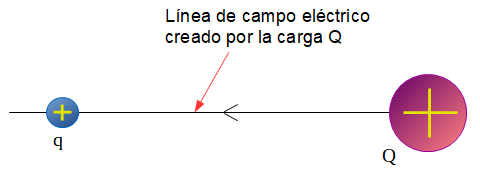
Figura 3. Cuerpo Q que genera un campo eléctrico en el que se encuentra a otra carga Q.
Es necesario aplicar una fuerza, es decir, realizar un trabajo para mover un cuerpo cargado contra el campo eléctrico. De este modo, la energía potencial eléctrica del cuerpo cargado aumenta si se realiza trabajo para moverlo en contra de un campo eléctrico.
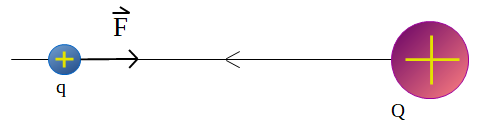
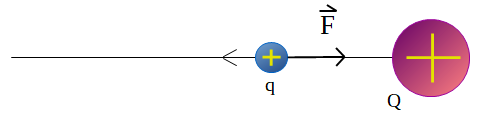
Figura 4. Cuerpo q se mueve por la acción de una fuerza que se realiza en contra del campo eléctrico creado por el cuerpo Q.
Para poder acercar el cuerpo con carga q al cuerpo con carga Q, se le debe proporcionar energía para vencer la repulsión eléctrica. La fuerza aplicada realiza un trabajo al mover la carga en contra del campo eléctrico del cuerpo Q. El trabajo realizado es igual a la energía que adquiere el cuerpo q. Esa energía adquirida por q, que depende de la posición en la que se encuentra, se denomina energía potencial eléctrica. La energía potencial eléctrica que almacena el cuerpo q, será liberada y se transformará en energía cinética si se deja de aplicar la fuerza, en ese caso comenzará a moverse hacia la izquierda aumentando su velocidad.
Si en vez de empujar un cuerpo con carga q, si se empujan dos cuerpos con cargas q, se tiene que realizar el doble de trabajo. De esta forma, dos cargas en una posición van a tener el doble de energía potencial eléctrica que una sola, así tres cuerpos con carga q tendrán el triple de energía potencial eléctrica y así sucesivamente. Resulta de utilidad definir el concepto de diferencia de potencial eléctrico, que consiste en considerar la energía potencial eléctrica por unidad de carga.
5. ¿Qué es la diferencia de potencial o voltaje?
La diferencia de potencial eléctrico, también llamada voltaje o tensión se define como:
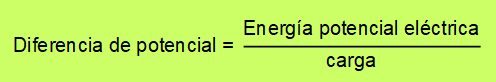
Esta energía potencial eléctrica, se la proporciona el campo eléctrico a las cargas. El campo eléctrico realiza trabajo sobre las cargas para que ellas se desplacen entre dos puntos.
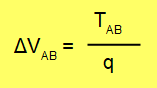
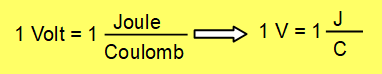
5.1. Ejemplo
En Uruguay la tensión o voltaje que brinda UTE es 230 V, esto significa que una carga de 1 C que se desplace de un terminal a otro del enchufe recibirá 230 J de energía del campo eléctrico que existe entre los terminales. De esta forma, las cargas transferirán al aparato conectado la energía que reciben del campo eléctrico para que el aparato funcione.
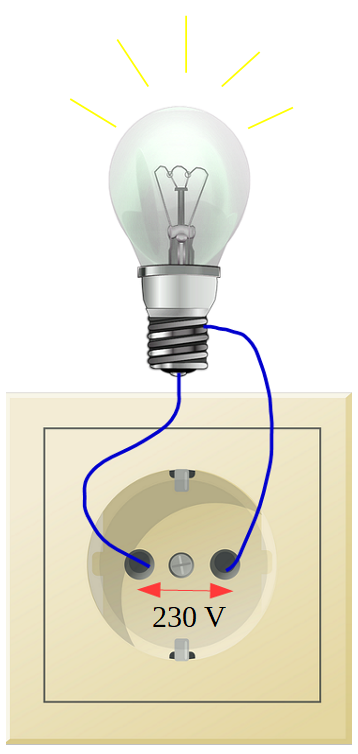
Figura 5. Lamparita conectada a un enchufe cualquiera del hogar mediante dos cables representados con color azul.
Una pila brinda 1,5 J de energía a cada Coulomb de carga que circula. Si se conecta una lamparita, ella va a transformar esa energía en luz y calor.
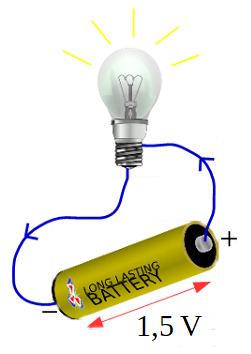
Figura 6. Lamparita conectada a una pila mediante dos cables representados con color azul.
6. Circuito eléctrico
Un circuito eléctrico es un recorrido cerrado con el fin de llevar energía eléctrica desde los elementos que la "producen", pilas, baterías y generadores, hasta otros elementos, los receptores, que la transforman en otro tipo de energía.
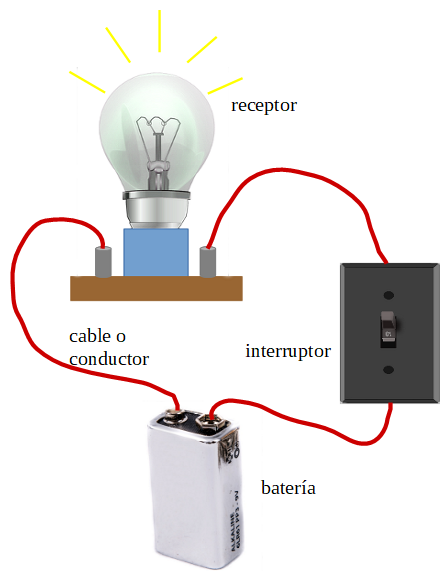
Figura 7. Circuito simple.
6.1. Elementos de un circuito eléctrico
Los elementos de un circuito eléctrico tienen diferentes funciones y símbolos. A continuación verás cómo se representan.
| Elemento | Nombre | Símbolo | Función |
|---|---|---|---|
 |
cable conductor |
 |
a través de sus electrones se transporta la energía eléctrica |
 |
interruptor |
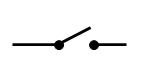 |
permitir o impedir el pasaje de corriente eléctrica |
 |
pila |
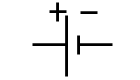 |
aportar energía eléctrica al circuito |
 |
batería |
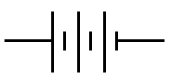 |
aportar energía eléctrica al circuito |
| |
fuente variable |
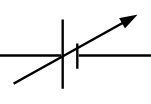 |
aportar energía eléctrica al circuito, permite modificar el valor de energía entregada por unidad de carga |
 |
lámpara |
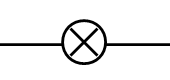 |
transformar energía eléctrica en luz y calor |
 |
resistor |
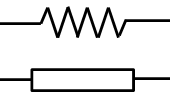 |
transformar energía eléctrica en calor |
| resistor variable |
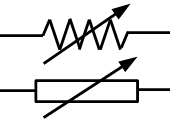 |
transformar energía eléctrica en calor |
|
 |
diodo |
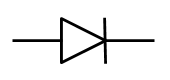 |
dispositivo semiconductor que
permite el paso de la corriente eléctrica en una única dirección con
características similares a un interruptor |
 |
amperímetro | 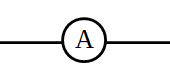 |
medir la intensidad de corriente |
 |
voltímetro |
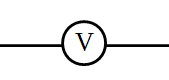 |
medir la diferencia de potencial entre dos puntos del circuito |
7. ¿Cómo se mide la intensidad de corriente en un circuito eléctrico?
Si se desea medir la intensidad de corriente en un circuito se necesitará un instrumento llamado amperímetro. Este instrumento se conecta en serie. En la figura a continuación se muestra un circuito sencillo en el que se ve un resistor conectado en serie a una pila y en el que se conectó también un amperímetro en serie para medir la intensidad de corriente, se representó además el sentido convencional de la corriente eléctrica en cada tramo. Este circuito tiene una sola malla, ya que la corriente solamente puede circular en un recorrido único.
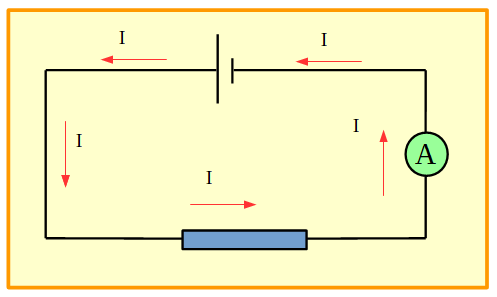
Figura 8. Circuito sencillo con un amperímetro.
En un circuito con más de un receptor conectado en serie, la intensidad corriente al igual que en el circuito sencillo solo tiene un camino posible. Es por este motivo, que los amperímetros que se han conectado en la figura medirán todos el mismo valor. Por lo tanto, en un circuito como este, con un solo amperímetro bastará para medir la intensidad de corriente en cada receptor.
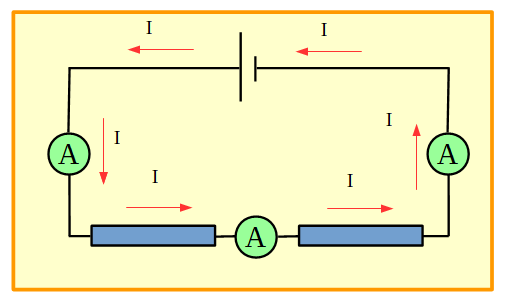
Figura 9. Circuito con dos resistores en serie.
Si los receptores ahora se conectan en paralelo:
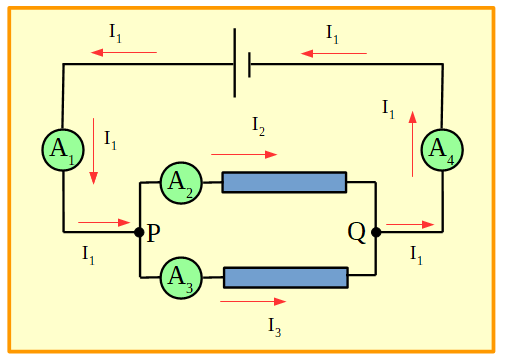
Figura 10. Circuito con dos resistores en paralelo.
En un circuito con receptores conectados en paralelo, es necesario colocar un amperímetro en cada rama del paralelo, en este caso A2 y A3.También se, colocaron los amperímetros A1 y A4 que están conectados en serie con la pila, éstos medirán el mismo valor de intensidad de corriente, I1, ya que se encuentran conectados en serie entre sí. Es así que la intensidad de corriente, I1 al llegar al nudo P se divide en I2 e I3. A su vez, I2 e I3 al llegar al nudo Q, se vuelven a sumar para formar nuevamente I1. Por lo tanto, en un circuito como este, serán necesarios sólo uno de los amperímetros A1 o el A4 (no los dos) , para medir la I1, y los amperímetros A2 y A3 para medir las I2 e I3.
Es así que en este caso: I1 = I2 + I3
Esto se puede generalizar en la Ley de los nudos, que expresa que la suma de las intensidades de corriente que llegan a un nudo es igual a la suma de las intensidades de corriente que salen de él.

7.1. Ley de los nudos y la conservación de la carga eléctrica
El siguiente circuito muestra dos resistores conectados en paralelo a una pila con las intensidades de corriente indicadas en cada zona:
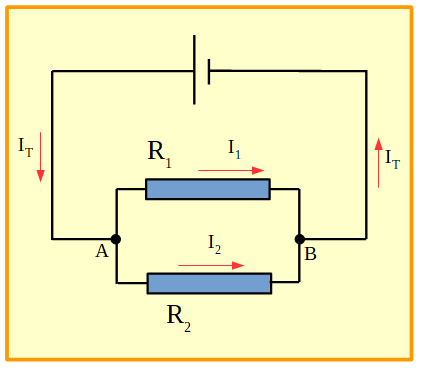
Figura 11. Circuito en paralelo con las intensidades de corriente indicadas.
Si se aplica la ley de los nudos para el nudo A se obtiene:
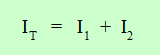
Considerando el concepto de intensidad de corriente: 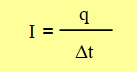
A la carga que circula antes del nudo A se le llama qT, q1 a la carga que circula por R1 y q2 a la carga que circula por R2. Así:
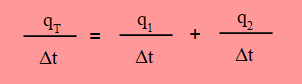
Al tomar un mismo intervalo de tiempo, se puede simplificar Δt en ambos miembros de la ecuación, por lo tanto llegamos a:
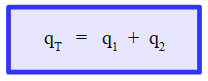
Es decir, la carga que llega al nudo A se divide en cada rama del circuito, de forma que la suma en cada rama es igual a la que llegó. Esto significa que la carga se conserva.
Lo mismo sucede en el nudo B: 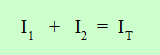 . La suma de las intensidades de corriente que llegan a un nudo es igual a la suma de las intensidades de corriente que salen de él.
. La suma de las intensidades de corriente que llegan a un nudo es igual a la suma de las intensidades de corriente que salen de él.
8. ¿Cómo se mide la diferencia de potencial entre dos puntos de un circuito eléctrico?
Si se desea medir la diferencia de potencial, ΔV, en los extremos de una pila y de un resistor, se debe conectar un voltímetro en paralelo a la pila en los puntos A y D y otro voltímetro en paralelo al resistor en los puntos B y C, como muestra la figura:
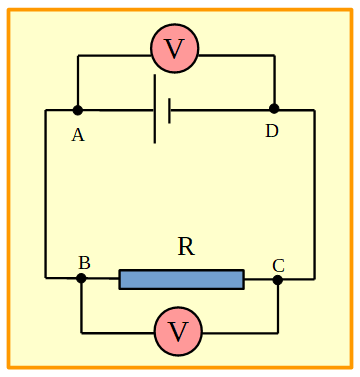
Figura 12. Circuito sencillo con un voltímetro en paralelo al resistor y a la pila.
Estos voltímetros medirán, la cantidad de energía que aporta la pila por unidad de carga y la cantidad de energía transformada en el resistor por unidad de carga eléctrica. Se puede ver que la cantidad de energía que aporta la pila por unidad de carga, es transformada en el único resistor conectado y por lo tanto: ΔVAD = ΔVBC.
Caso de resistores conectados en serie
En el caso que se tenga un circuito con dos o más elementos conectados en serie y se desee medir la diferencia de potencial en cada uno de los elementos conectados, se deberá conectar un voltímetro en los extremos de cada uno de ellos, tal como muestra la figura que sigue:
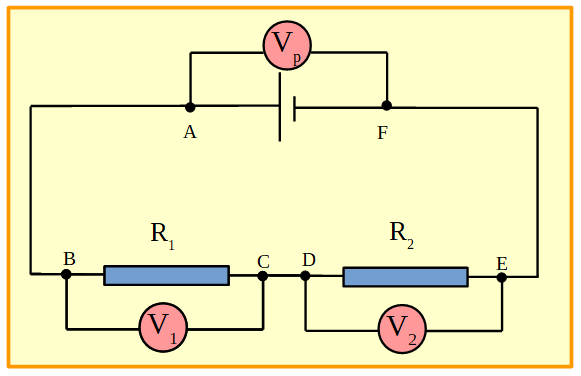
Figura 13. Circuito en serie con dos resistores y una pila. Se conectaron voltímetros en los extremos de cada elemento.
- Vp, mide la ΔVAF, en los extremos de la pila,
- V1, mide la ΔVBC, en los extremos de R1 y el,
- V2 mide la ΔVDE, en los extremos de R2.
- ΔVAF = ΔVBE
- ΔVBE = ΔVBC + ΔVCE → ΔVAF = ΔVBC + ΔVCE
Si ahora se quiere medir la diferencia de potencial en los extremos de elementos conectados en paralelo, se deberán conectar voltímetros como muestra la figura:
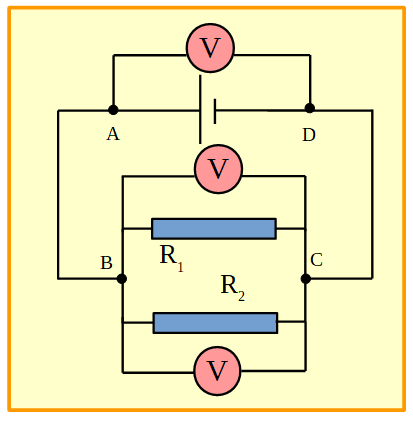
Figura 14. Circuito en paralelo con dos resistores y una pila. Se conectaron voltímetros en los extremos de cada elemento.
Los puntos A y B se encuentran al mismo potencial eléctrico debido a que entre ellos no se encuentra conectado ningún elemento que aporte o transforme energía eléctrica. La misma situación sucede entre los puntos C y D. Por esto se concluye que:
ΔVAD = ΔVBC
De esta manera, elementos cualquiera conectados en paralelo van a tener la misma diferencia de potencial en sus extremos y bastará con un sólo voltímetro conectado en paralelo para poder medir en sus extremos la ΔV.
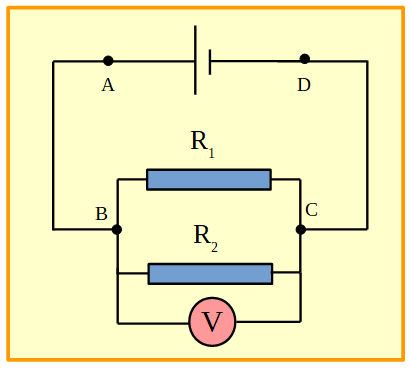
Figura 15. Circuito en paralelo con dos resistores y una pila. Se conectó un voltímetro entre los puntos B y C.
8.1. Ley de las mallas y la conservación de la energía en un circuito
Primero se explica qué es una malla. Una malla es un camino cerrado formado por elementos en un circuito. Por ejemplo, en la siguiente figura se muestra un circuito con una sola malla.
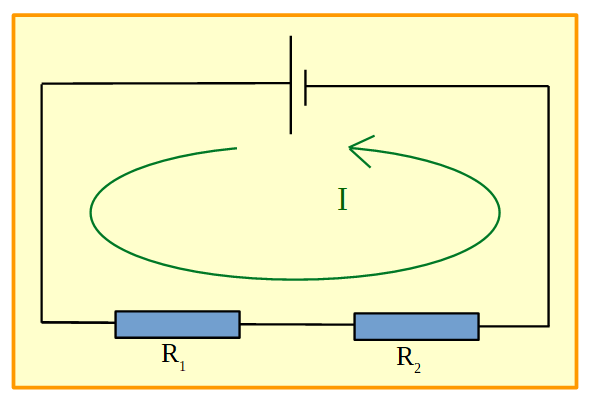
Figura 16. Circuito con una sola malla.
En este circuito hay un elemento que aporta energía eléctrica, la pila, y dos elementos que transforman esa energía en calor, los resistores. Si se recorre el circuito en el sentido convencional de la corriente, como está indicado en la figura, la diferencia de potencial (por convención) de la pila, se tomará positiva +ΔVp y las diferencias de potencial de cada resistor se tomarán negativas: -ΔV1 y -ΔV2.
La ley de las mallas expresa que la suma de las diferencias de potencial en una malla es igual a cero. Para la situación de la figura:
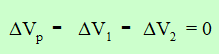
Si se considera el concepto de ΔV:
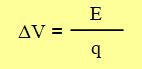
La carga q que circula por el circuito por unidad de tiempo es igual en todo el circuito (circuito en serie), se la nombra q. A la energía que aporta la pila se la nombra Ep, a la que se transforma en el resistor R1, E1 y a la que se transforma en el resistor R2, E2.
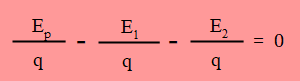
Se puede observar que la carga q divide en todos los términos y por tanto se puede simplificar quedando:
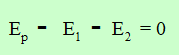
Lo cual significa que la energía se conserva, ya que la energía aportada por la pila es transformada en cada uno de los elementos, es decir:
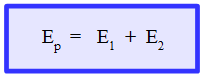
Esto significa que la energía se conserva en una malla. La energía aportada por la fuente se transforma en cada uno de los elementos de dicha malla.

Si en la malla hay más elementos conectados se agregan las diferencias de potencial que correspondan a ellos.
8.2. Circuito en paralelo y la ley de las mallas
Si consideramos el siguiente circuito:
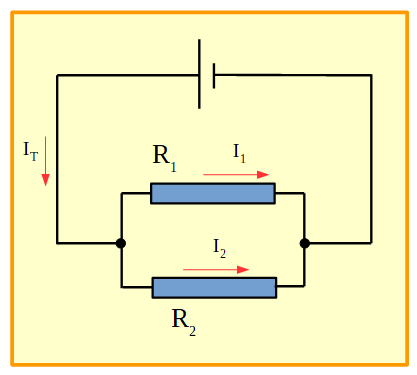
Figura 17. Circuito en paralelo.
Podemos ver que son posibles tres recorridos cerrados, es decir, este circuito posee tres mallas. Para cada una de las mallas aplicaremos lo visto antes:
Malla 1
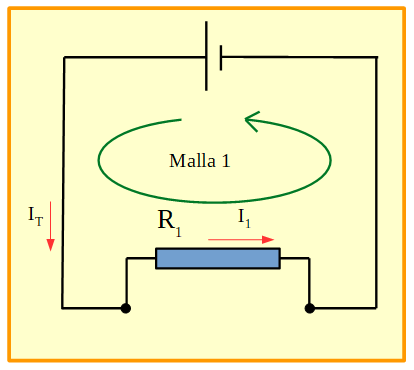
Figura 18. Circuito en el que se muestra la malla 1.
Si aplicamos la ley de las mallas para la malla 1, queda:
es decir que:
tal como vimos anteriormente para un circuito en paralelo.
Malla 2
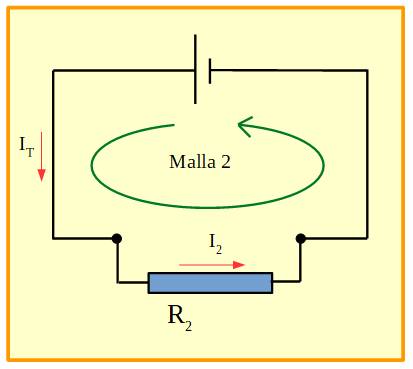
Figura 19. Circuito en el que se muestra la malla 2.
Si aplicamos la ley de las mallas para la malla 1, queda:
es decir que:
tal como vimos anteriormente para un circuito en paralelo.
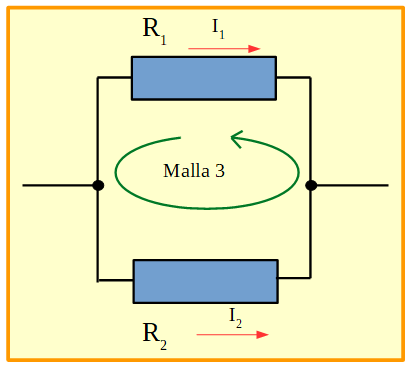
Figura 20. Circuito en el que se muestra la malla 3.
En esta última malla tenemos que hacer la siguiente aclaración: Si recorremos alguna parte del circuito en sentido opuesto al de la corriente convencional, el signo de la diferencia de potencial en los extremos del elemento que se encuentre en dicha zona, será opuesto al que le asignamos si recorremos en el sentido de la corriente convencional. En el caso de este ejemplo queda:
por lo tanto:
tal como vimos anteriormente. La diferencia de potencial de elementos conectados en paralelo, es la misma.
9. Resistencia eléctrica
La resistencia eléctrica es una magnitud física que indica la oposición que presentan los materiales al paso de la corriente eléctrica. Se simboliza con la letra R y su unidad de medida es el ohmio, Ω.
Los materiales conductores tienen poca resistencia, pues permiten que la corriente circule por ellos.
Los materiales aislantes presentan una elevada resistencia, tan alta que no permiten el paso de los electrones.
Todos los receptores (lámparas, motores, etc.) que se conecten en un circuito tienen resistencia, por lo tanto, a los electrones les resulta más difícil circular por ellos.
La resistencia de un elemento se puede determinar si se mide la diferencia de potencial en sus extremos y la intensidad de corriente que circula por él:
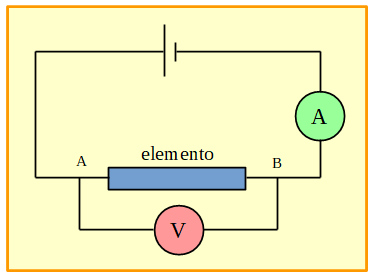
Figura 21. Circuito con un elemento, una pila, un amperímetro y un voltímetro.
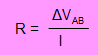
9.1. Resistencia eléctrica de un conductor
La resistencia eléctrica de un conductor depende del material del mismo y de la forma que tiene.
La resistividad es una propiedad intensiva característica, cada material tiene su valor de resistividad a determinada temperatura. Esta magnitud se representa con la letra griega Rho, ρ.
A menor resistividad, el material es mejor conductor eléctrico, por lo tanto, va a tener menor resistencia eléctrica. La siguiente tabla muestra las resistividades de diferentes materiales, observar que la plata y el cobre son los materiales que tienen menor resistividad, por tanto son buenos conductores. El ámbar y el cuarzo tienen resistividades muy elevadas, por tanto se pueden considerar como aislantes.
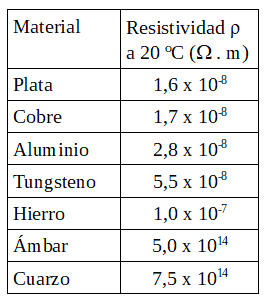
Tabla 2. Resistividades de diferentes materiales a 20 ºC.
La resistencia también depende del largo y del área de la sección que tenga el conductor. Cuanto más largo y más fino sea el conductor, mayor va a ser su resistencia.
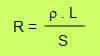
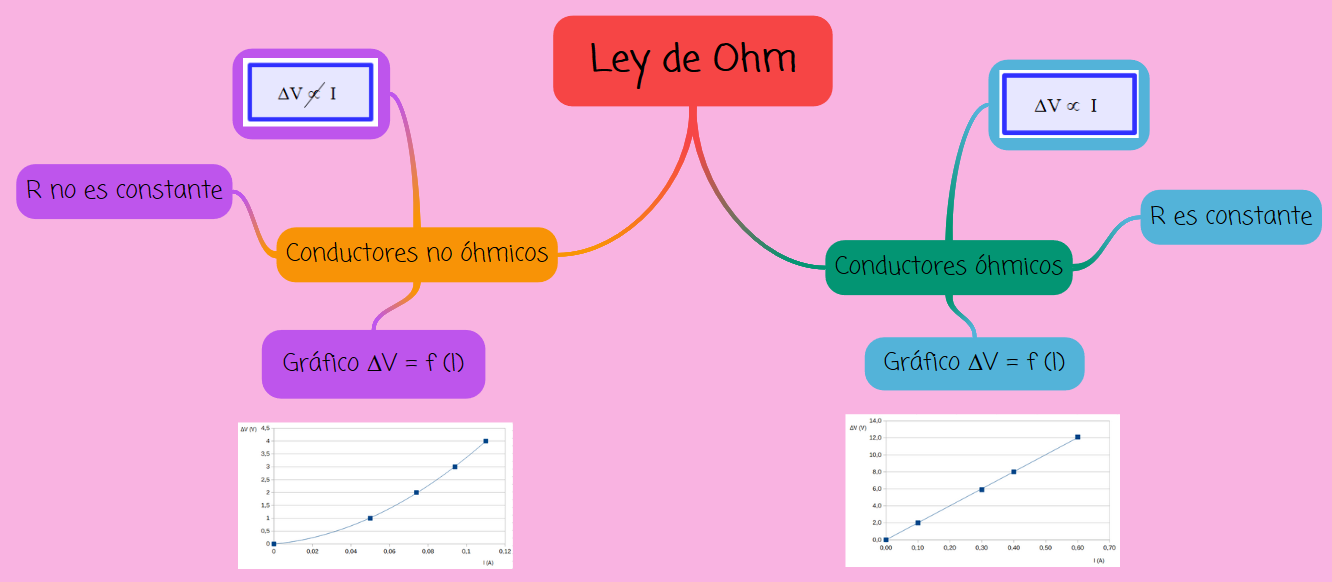
9.2. Ley de Ohm
Los elementos de un circuito pueden tener resistencia variable o constante dentro de determinados parámetros.
Supón que conectamos el siguiente circuito:
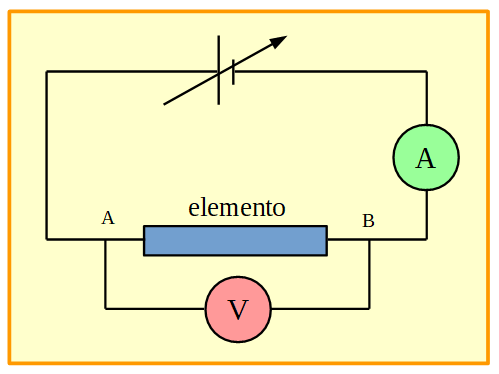
Figura 22. Circuito con un elemento, una fuente variable, un amperímetro y un voltímetro.
La fuente variable permite modificar la diferencia de potencial en los extremos del elemento y la intensidad de corriente que lo atraviesa.
Para un resistor, se va modificando (utilizando la fuente variable) la diferencia de potencial en sus extremos (registrando su valor con el voltímetro conectado en paralelo) y se mide la intensidad de corriente (con el amperímetro conectado en serie al resistor). Se puede construir una tabla de valores como se muestra:
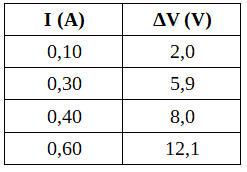
Tabla 3. Valores de intensidad de corriente y diferencia de potencial en los extremos de un resistor.
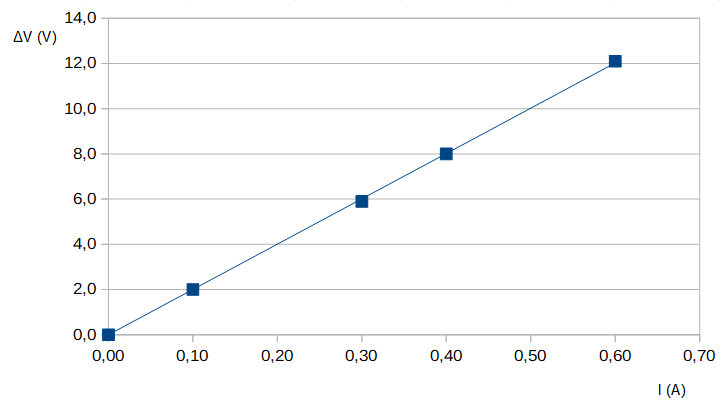
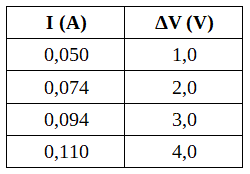
Tabla 4. Valores de intensidad de corriente y diferencia de potencial en los extremos de una lamparita.
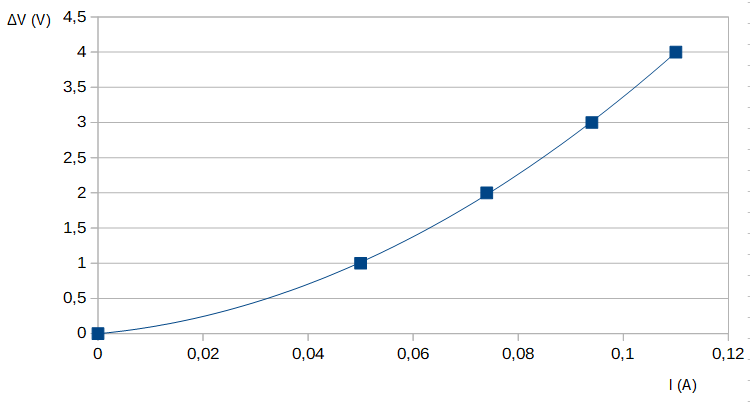
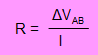
10. Potencia eléctrica
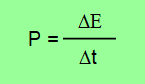
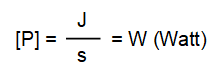
11. Créditos
Bibliografía
- Alvarenga, B. y Máximo, A. (1997). Física general. México: Oxford University.
- Egaña, E; Berruti, M. y González, A. (2014). Interacciones 4. Campos y ondas. Uruguay: Contexto.
- Hewitt, P. (2007). Física conceptual. México: Pearson-Addison Weasley.
Imágenes, sitios, simuladores y videos
- Plantilla colección-banner-vector_3893107. Autor: Vector_corp, Freepik. Licencia Estándar de Freepik.
- Plantilla Canva. Autor: Canva.com. Recuperado de: https://www.canva.com/design/DADthPVpscE/share/preview?token=y_nyiv4U3URdphSUaGnLOA&role=EDITOR&utm_content=DADthPVpscE&utm_campaign=designshare&utm_medium=link&utm_source=sharebutton
- Pastel Graffiti Gift Tag. Autor: Canva.com. Recuperado de: https://www.canva.com/design/DADthdYFvLc/8572_ip2Ap9jwAy4RKRF6Q/view?utm_content=DADthdYFvLc&utm_campaign=designshare&utm_medium=link&utm_source=sharebutton
- Enchufe. Autor: OpenCliplart-Vectors/27427 en Pixabay. Licencia: Pixabay.
- Bombilla. Autor: Alefonte en Pixabay. Licencia: Pixabay.
- Foto de fuente variable. Autor: Desconocido, en Pxhere. Licencia: CC0.
- Batería. Autor: Clker-Free-Vector-Images/29588 en Pixabay. Licencia: Pixabay.
- Cable conductor. Autor: Stefan Riepl en Wikipedia. Licencia: CC BY-SA 3.0.
- Pila. Autor: Maxpower148 en Pixabay. Licencia: Pixabay.
- Interruptor de luz. Autor: Clker-Free-Vector-Images/29588 en Pixabay. Licencia: Pixabay.
- Batería. Autor: Clker-Free-Vector-Images/29588 en Pixabay. Licencia: Pixabay.
- 1.5 ohm 5 % axial resistor.jpg. Autor: Oomlout en Wikimedia commons. Licencia: CC BY-SA 2.0.
- Variable resistor.jpg. Autor: Meganbeckett27 en Wikimedia commons. Licencia: CC BY-SA 3.0.
- Diodo. Autor: Willtron en Wikipedia. Licencia: CC BY-SA 3.0.
- Amperímetro. Autor: Clker-Free-Vector-Images/29588 en Pixabay. Licencia: Pixabay.
- Voltímetro. Autor: Clker-Free-Vector-Images/29588 en Pixabay. Licencia: Pixabay.
- Batería de nueve voltios. Autor: George Hodan en Public Domain. Pictures. net. Licencia: Dominio Público CC0.
- Las imágenes con los símbolos de los circuitos fueron creadas por la autora del recurso utilizando Open Office y su licencia es CC BY-SA 4.0.
- Anteldetodos
(2014). Micro Antel Ciencias: Corriente eléctrica. Recuperado de: https://www.youtube.com/watch?v=dQuoJouqFXQ. Licencia Estándar de
YouTube.
Autoría del Módulo: Silvia Pedreira.
spedreira@uruguayeduca.edu.uy