Lentes

Sitio:	Aulas \| Uruguay Educa
Curso:	Física - 1º B.D.
Libro:	Lentes
Imprimido por:	Invitado
Día:	martes, 7 de mayo de 2024, 07:00

Tabla de contenidos

1. Iniciamos repasando lo visto en 1er año de Ciclo Básico
2. Lentes delgadas
3. Lente biconvexa: Lupa
4. Rayos principales lentes biconvexas
- 4.1. Formación de imágenes lentes biconvexas
- 4.2. Simulamos la formación de imágenes en una lente biconvexa
5. Lentes bicóncavas
6. Créditos

1. Iniciamos repasando lo visto en 1er año de Ciclo Básico

Te sugiero que comiences repasando los conceptos vistos en 1er año de Ciclo Básico sobre las lentes en el siguiente sitio.

Revisa todos los materiales del módulo y realiza las actividades que se proponen.

2. Lentes delgadas

La óptica geométrica explica la formación de imágenes de una forma muy sencilla para lentes delgadas, (es decir, para radios de curvatura grandes). En esta aproximación del modelo, se desprecia el espesor de la lente (lente delgada) y los rayos forman ángulos pequeños con el eje principal de la lente. De esta forma, no es necesario considerar la refracción en cada una de las caras de la lente.

Es importante tener en cuenta, que si la lente no se puede considerar delgada o si los rayos no forman ángulos pequeños, este modelo no será válido y se producirán aberraciones en las imágenes.

Diagrama de una lente biconvexa:

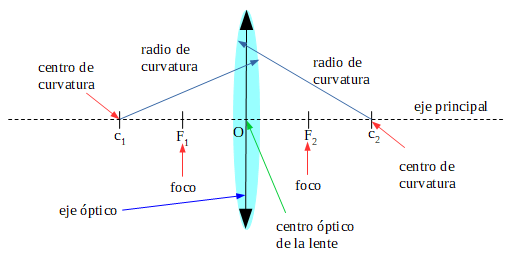
Esquema de una lente biconvexa, en ella se indican los centros de curvatura, los radios de cada cara de la lente, el eje principal, los focos y el centro óptico de la lente

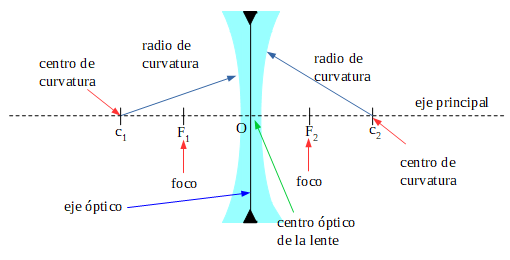
Diagrama de una lente bicóncava:

Esquema de una lente bicóncava, en ella se indican los centros de curvatura, los radios de cada cara de la lente, el eje principal, los focos y el centro óptico de la lente

Se definen:

Los centros de curvatura C₁ y C₂, corresponden a los centros de cada una de las caras esféricas que forman la lente. La distancia desde estos puntos a la cara es el radio de curvatura.
El eje principal, es la recta que une los centros de curvatura. Es un eje de simetría de la lente.
El eje óptico, es el eje de simetría entre las caras de la lente.
El centro óptico, es el centro geométrico de la lente, es el punto en el que se corta el eje principal y el eje óptico.
La distancia del foco al eje de óptico se denomina distancia focal. La distancia focal es la mitad del radio de curvatura.

En las lentes delgadas o lentes simples, se establece el comportamiento de tres rayos, llamados rayos principales, para la construcción de las imágenes.

3. Lente biconvexa: Lupa

La lupa es un instrumento óptico interesante y simple, se trata de una lente biconvexa y forma diferentes tipos de imágenes dependiendo de la distancia entre el objeto que se desea observar, la lupa y el observador.

La lupa es una lente gruesa, en la que los radios de curvatura de las caras son relativamente pequeños. Esto resulta en que si observamos a través de las zonas próximas al borde de la lupa la imagen se ve distorsionada. Esto se denomina aberración óptica y es una falla del modelo de la lente delgada. En el siguiente video se observan las imágenes que se pueden formar al mirar a través de una lupa (tener en cuenta que las distorsiones en la imagen son debidas a la aberración antes mencionada).

Video recuperado de: https://youtu.be/KoeP9WQOF5I. Licencia: Creative Commons-Atribución.

Música del video: Evening Fly of the Brants A (ID 950). Álbum: Window Forecasts. Autor: Lobo Loco. Licencia: Creative Commons.

4. Rayos principales lentes biconvexas

Los rayos principales o de trayectoria definida, son útiles para estudiar la formación de las imágenes en las lentes.

A continuación se muestran los tres rayos principales:

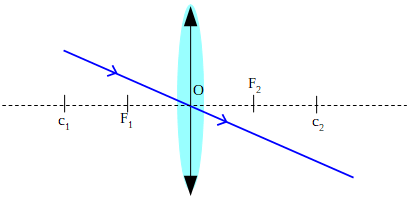
Rayo paralelo: todo rayo que incide paralelo al eje principal, se refracta pasando por el foco.

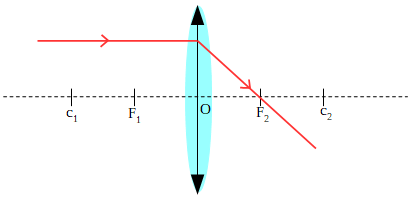
$Rayo que incide paralelo al eje principal se refracta pasando por el foco 2$

Rayo focal: cualquier rayo que incida en la dirección de uno de los focos, se refracta paralelo al eje principal.

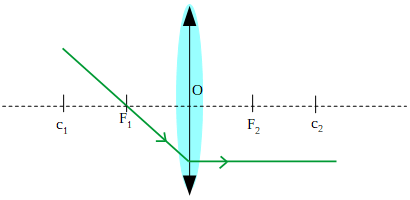
$rayo que incide pasando por el foco se refracta paralelo al eje principal$

Rayo central: cualquier rayo que incida en la dirección del centro óptico, no se refracta, atraviesa la lente sin desviarse.

$Rayos que inciden en la dirección del centro óptico, no se refractan, atraviesan la lente sin desviarse.$

4.1. Formación de imágenes lentes biconvexas

Las características de las imágenes formadas por las lentes biconvexas cambian dependiendo de dónde esté ubicado el objeto con respecto a la lente. A continuación se muestran los diferentes casos y se explican las características de la imagen que se forma.

Objeto ubicado entre el foco y el centro óptico

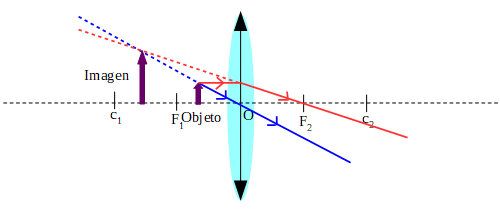
Objeto ubicado entre el foco y la lente, forma una imagen de mayor tamaño ubicada entre el foco y el centro

La imagen se encuentra entre el foco y el centro de curvatura, es derecha, de mayor tamaño que el objeto y es virtual (se forma con la intersección de las prolongaciones de los rayos refractados y no es posible proyectarla en una pantalla).

Objeto ubicado en el foco

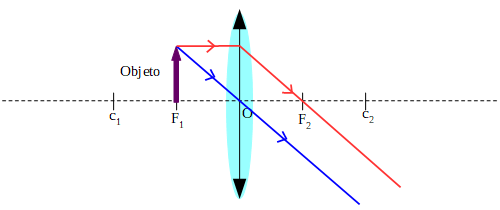
$Objeto ubicado en el foco, los rayos refractados son paralelos, no se forma imagen$

En este caso no se forma imagen, ya que los rayos que atraviesan la lente son paralelos, por lo tanto no se cortan ellos ni sus prolongaciones.

Objeto ubicado entre el centro de curvatura y el foco

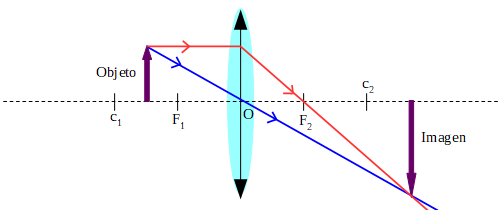
Objeto ubicado entre el foco y el centro de curvatura forma una imagen invertida, real y de mayor tamaño que el objeto

En este caso la imagen es real (se puede proyectar en una pantalla, se forma con la intersección de los rayos que atraviesan la lente), es invertida y de mayor tamaño con respecto al objeto.

Objeto ubicado en el centro de curvatura

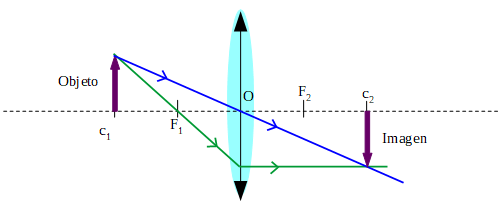
Objeto ubicado en el centro de curvatura forma una imagen ubicada en el otro centro de curvatura, de igual tamaño, real e invertida

Aquí la imagen que se forma en el otro centro de curvatura, es real, invertida y de igual tamaño que el objeto.

Objeto ubicado a una distancia mayor que el radio de curvatura

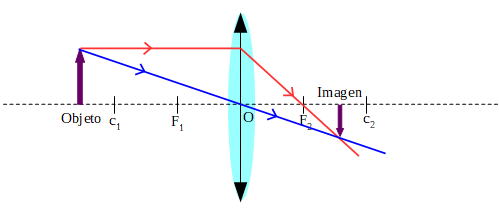
Objeto ubicado a una distancia mayor que el radio de curvatura forma una imagen ubicada entre el foco y el otro centro de curvatura, real, invertida y de menor tamaño que el objeto.

La imagen se ubica entre el foco y el otro centro de curvatura, es real, invertida y de menor tamaño que el objeto.

4.2. Simulamos la formación de imágenes en una lente biconvexa

Ingresa al siguiente simulador en GeoGebra y sigue los siguientes pasos para observar la formación de imágenes en una lente biconvexa: https://www.geogebra.org/m/dpFzRedt

Elige que la lente sea biconvexa deslizando el botón gris con centro negro hacia la izquierda.
Haz clic sobre el extremo del objeto (punto morado) y muévelo de forma de colocarlo en las posiciones vistas en el capítulo anterior.
Puedes probar de cambiar la posición del foco y el tamaño de la lente.

5. Lentes bicóncavas

Las lentes biconcavas, se caracterizan por ser más gruesas en los bordes que en el centro. Son lentes divergentes, cuando un haz de rayos paralelos la atraviesan, éstos se refractan de forma que divergen y las prolongaciones de los rayos refractados se cortan en el foco 1.

$lente bicóncava en la que inciden cuatro rayos paralelos al eje principal, éstos se refractan al atravesar la lente de forma divergente y sus prolongaciones se cortan en el foco 1.$

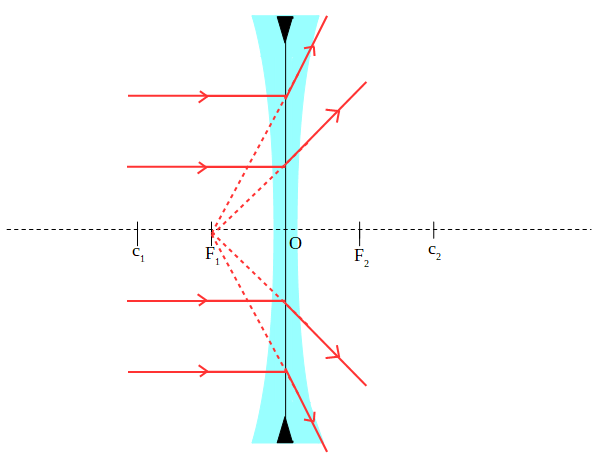
Se utilizan para corregir defectos en la visión, por ejemplo miopía.

5.1. Rayos principales lentes bicóncavas

Los rayos principales de las lentes bicóncavas se llaman de la misma forma que los de las lentes biconvexas, pero funcionan un poco diferente.

A continuación se explican los tres rayos principales de estas lentes:

Rayo paralelo: es cualquier rayo que incide paralelo al eje principal y se refracta de modo que su prolongación tiene la dirección del foco 1.

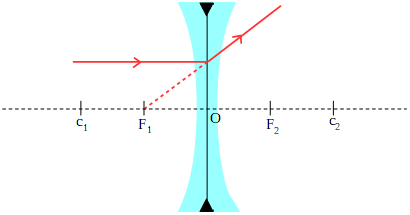
$Rayo paralelo, incide paralelo al eje principal y se refracta de modo que su prolongación pasa por el foco 1$

Rayo focal: cualquier rayo que incide de modo que su prolongación pasa por el foco 2 y se refracta paralelo al eje principal.

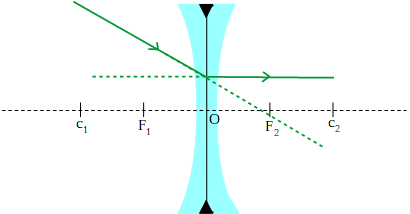
$Rayo focal: incide de modo que su prolongación pasa por el foco 2 y se refracta paralelo al eje principal.$

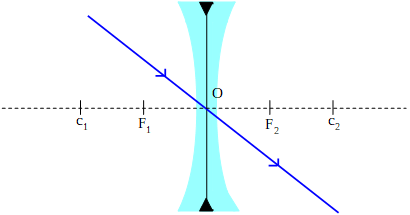
Rayo central: cualquier rayo que incida en la dirección del centro óptico, no se refracta, atraviesa la lente sin desviarse.

$cualquier rayo que incida en la dirección del centro óptico, no se refracta, atraviesa la lente sin desviarse.$

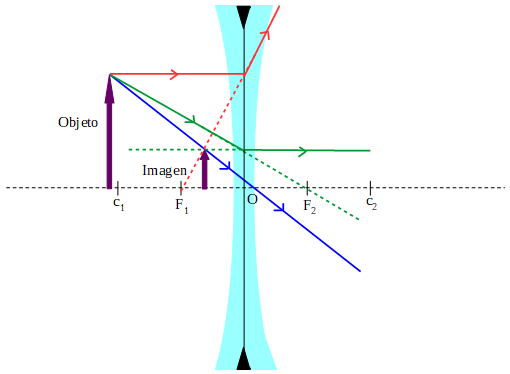
5.2. Formación de imágenes lentes bicóncavas

Las lentes bicóncavas sólo forman un tipo de imagen, sin importar en qué lugar se encuentre el objeto con respecto a la lente. Las características de la imagen para este tipo de lente siempre serán: virtual, derecha y de menor tamaño que el objeto.

$Objeto ubicado frente a una lente bicóncava, su imagen se forma con la intersección de las prolongaciones de los rayos refractados, es virtual, derecha y de menor tamaño que el objeto.$

5.3. Simulamos la formación de imágenes en una lente bicóncava

Ingresa al siguiente simulador en GeoGebra y sigue los siguientes pasos para observar la formación de imágenes en una lente bicóncava: https://www.geogebra.org/m/dpFzRedt

Elige que la lente sea bicóncava.
Haz clic sobre el extremo del objeto (punto morado) y muévelo de forma de colocarlo en diferentes posiciones de forma de verificar lo dicho en el capítulo anterior.
Puedes probar de cambiar la posición del foco y el tamaño de la lente.

6. Créditos

Bibliografía

Cabeza, C.; Núñez, I. (2003). Curso de Actualización Docente. Programa de Física 2003 para 1er año de Bachillerato en Educación Secundaria. Facultad de Ciencias. Instituto de Física. Universidad de la República. Pedeciba.
Alvarenga, B. y Máximo, A. (1997). Física general. México: Oxford University.
Egaña, E; Berruti, M. y González, A. (2014). Interacciones 4. Campos y ondas. Uruguay: Contexto.
Hewitt, P. (2007). Física conceptual. México: Pearson-Addison Weasley.

Imágenes, sitios, simuladores y videos

Módulo de aprendizaje: Lentes de 1er año de Ciclo Básico. Autores: Gatto, A., Pedreira, S. y otros. Portal Uruguay Educa. Recuperado de: http://aulas.uruguayeduca.edu.uy/course/view.php?id=218&section=8. Licencia: CC BY-SA 4.0.
Lupa. Autor: Silvia Pedreira. Recuperado de: https://youtu.be/KoeP9WQOF5I. Licencia: Creative Commons-Atribución.
Música del video Lupa: Evening Fly of the Brants A (ID 950). Álbum: Window Forecasts. Autor: Lobo Loco. Licencia: Creative Commons.
GeoGebra, Lente convergente / divergente. Autor: Jesús Benayas Yepes. Licencia: CC BY-NC-SA 4.0.

Autoría del Módulo: Silvia Pedreira.

spedreira@uruguayeduca.edu.uy

Esta obra está bajo una Licencia Creative Commons Atribución 4.0 Internacional.

Portal Uruguay Educa.

Diciembre de 2019.