Ondas en una y dos dimensiones y sus fenómenos

Sitio:	Aulas \| Uruguay Educa
Curso:	Física - 1º B.D.
Libro:	Ondas en una y dos dimensiones y sus fenómenos
Imprimido por:	Invitado
Día:	lunes, 29 de abril de 2024, 19:10

Tabla de contenidos

1. Ondas en una dimensión - velocidad de propagación de un pulso
2. Autoevaluación de lo visto hasta aquí
3. Frente de onda
- 3.1. Representación de la propagación de una onda
4. Ondas periódicas
- 4.1. Magnitudes características de las ondas periódicas
- 4.2. Representación de ondas periódicas en dos dimensiones
5. Fenómenos ondulatorios en una y dos dimensiones
6. Principio de Huygens, para explicar la propagación de las ondas y los fenómenos
7. Ondas Bidimensionales - Resumen de sus fenómenos
8. Créditos

1. Ondas en una dimensión - velocidad de propagación de un pulso

Las ondas en una dimensión son las que se propagan en una única dirección, por ejemplo en cuerdas y resortes.

A continuación, estudiaremos la velocidad de propagación de un pulso en una cuerda tensa. Para ello, primero haremos un experimento simulado y veremos la influencia del aumento o disminución de la tensión en la velocidad de propagación.

Luego definiremos la densidad lineal de masa de una cuerda y su influencia en la velocidad de propagación.

Por último, veremos la relación matemática para determinar la velocidad de propagación de un pulso en una cuerda tensa, si se conocen la tensión a la que se somete la cuerda y la densidad lineal de masa de la misma.

1.1. Influencia de la tensión ejercida sobre la cuerda en la velocidad de propagación de un pulso que se propaga por ella

Para estudiar la velocidad de propagación de las ondas en una cuerda tensa usaremos un simulador. Con él visualizaremos la influencia de la tensión en la velocidad de propagación de la onda.

Elige la siguiente selección:

Pulso.
Sin Extremo.
Movimiento lento.
Amortiguación ninguna.
Reglas.
Cronómetro.

Con la tensión alta:

Coloca la regla en el extremo izquierdo de la cuerda, de modo que el punto verde quede centrado en el cero.
Arrastra el cronómetro bien cerca del símbolo (generar pulso).
Genera un pulso y acciona el cronómetro cuando el punto verde del extremo izquierdo de la cuerda alcance su altura máxima y detén el cronómetro cuando el pulso alcance su altura máxima a los 6 cm. Registra el valor del tiempo.
Repite el punto anterior, tres o cuatro veces y realiza un promedio de los valores de tiempo.
Determina la velocidad del pulso.

Con la tensión baja:

Repite los pasos anteriores (cuando la tensión era alta).

Elabora una conclusión basada en las observaciones y cálculos realizados, en cuanto a la relación entre la tensión a la que está sometida la cuerda y la velocidad de propagación del pulso por ella.

1.2. Densidad lineal de masa de una cuerda

Recuerda el concepto de densidad de un material. Si quieres repasar sobre densidad ingresa en http://aulas.uruguayeduca.edu.uy/course/view.php?id=218&section=12

La densidad lineal de masa de una cuerda es una propiedad intensiva.

Se simboliza con la letra griega mu, μ. Se define como el cociente entre la masa de la cuerda y su longitud.

ecuación del concepto de densidad lineal de masa igual a masa de la cuerda dividida la longitud de la cuerda.

es decir,

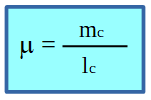
ecuación del concepto de densidad lineal de masa igual a masa de la cuerda dividida la longitud de la cuerda, de forma abreviada

La unidad de medida de la densidad lineal de masa en el S.I. es kg/m (kilogramos dividido metros).

[µ] = kg/m

1.3. Determinación de la velocidad de un pulso en una cuerda a partir de su densidad lineal de masa y de la tensión a la que es sometida

La relación matemática entre la tensión y la densidad lineal de masa, que permite determinar la velocidad de propagación de una onda en una cuerda tensa es:

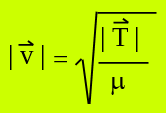
la velocidad de una onda en una cuerda tensa es igual a la raíz cuadrada de la tensión a la que es sometida, dividido entre la densidad lineal de masa de la cuerda.

Cuando realices las actividades experimentales 1 y 2, podrás verificar esta relación.

2. Autoevaluación de lo visto hasta aquí

3. Frente de onda

Antes de empezar a estudiar los fenómenos ondulatorios, analizaremos el concepto de frente de onda.

Un frente de onda es el conjunto de puntos del medio que son alcanzados en un mismo instante por un determinada onda. En el frente de onda el medio presenta el mismo estado de vibración, es decir, los "trocitos de medio" están en fase (recuerda que estar en fase significa tener igual elongación y velocidad)

Las ondas se pueden propagar en una dimensión, en dos dimensiones o en tres dimensiones, es así que los frentes de onda pueden adoptar diferentes formas. La energía que transporta la onda está asociada a la forma del frente de onda. Es importante aclarar que consideraremos que los medios son homogéneos (sus propiedades físicas y químicas son iguales) e isótropos (lo que significa que las direcciones de propagación son equivalentes).

En las imágenes a continuación se muestran algunos frentes de onda en una, dos y tres dimensiones.

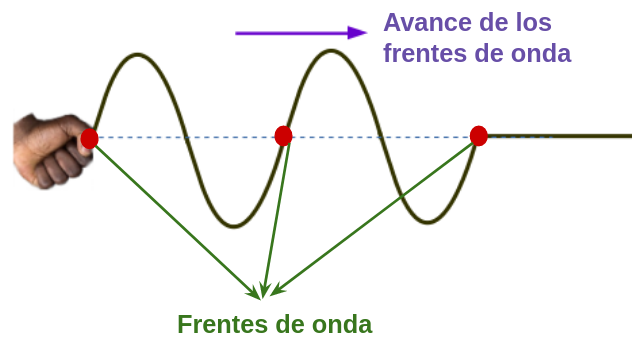
Se muestra el perfil de una cuerda por la que viaja una onda periódica que es agitada en su extremo por una mano, se indica el sentido de propagación de la onda y los puntos que representan el frente de onda

En las ondas unidimensionales, el frente de ondas está representado por un punto.

Se muestra gotas cayendo en la superficie el agua, se ven circulos concéntricos al lugar donde cae la gota que representan los frentes de onda.

En las ondas bidimensionales los frentes de onda pueden adoptar diferentes formas, dependiendo cómo sean generados. Por ejemplo, si es generado por una gota que cae en la superficie del agua, el frente de onda tendrá forma de circunferencia, cuyo centro estará en el lugar donde cae la gota.

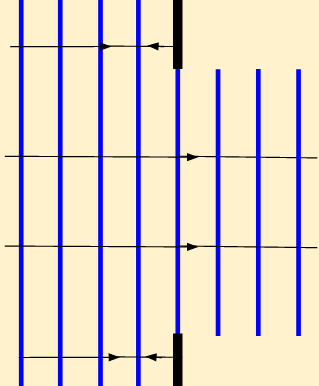
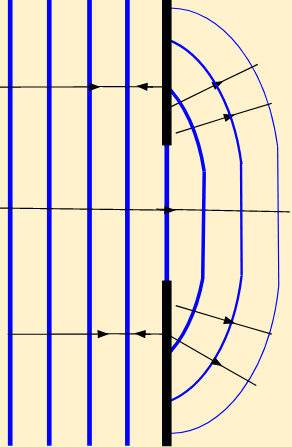
Si la onda es generada por una regla plana que agita el agua, la forma del frente de onda es de líneas planas y paralelas, a continuación se muestra la captura de pantalla del simulador de ondas de la Universidad de Colorado Boulder, en la que se indican los frentes de onda planos y paralelos entre sí.

Se muestra la captura de pantalla del simulador de ondas de la Universidad de Colorado Boulder, en la que se indican los frentes de onda planos y paralelos entre sí.

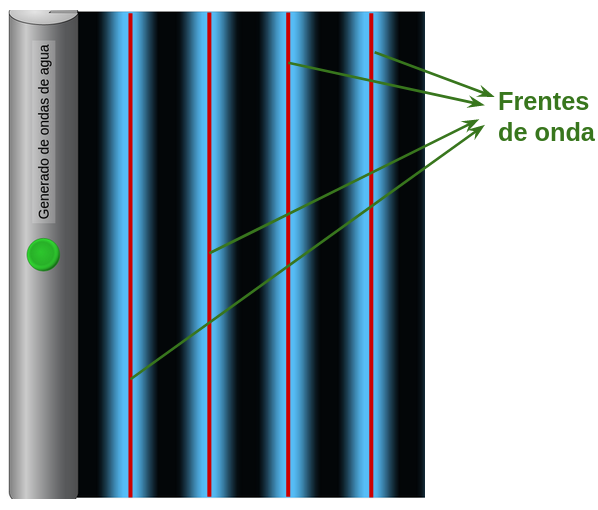
Frentes de onda planos y paralelos en la superficie del agua. Caso de una onda bidimensional.

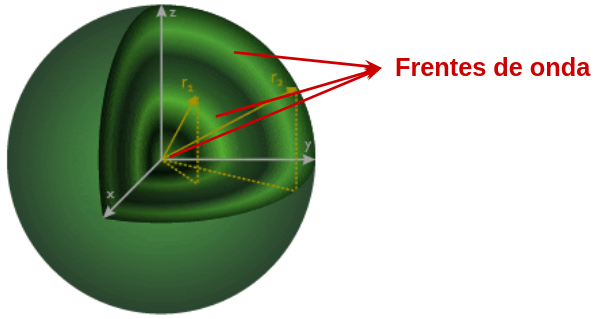
Se muestran ondas esféricas en las que se han indicado cuáles son los frentes de onda.

Los frentes de las ondas en tres dimensiones que son generadas por un foco puntual tienen forma de esferas concéntricas al lugar de generación.

También pueden darse frentes de ondas planos y paralelos en tres dimensiones. ¿Te imaginas cómo sería su imagen?

3.1. Representación de la propagación de una onda

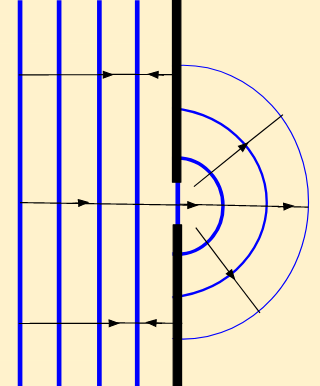
Por convención se representan las crestas de la onda con líneas llenas y los valles con líneas punteadas. Cuando se desea indicar la dirección y sentido de propagación de una onda en dos dimensiones se suelen utilizar líneas rectas orientadas (flechas) a las que se les llama rayos.

Estos rayos tienen dirección perpendicular al frente de onda. Observa las siguientes figuras:

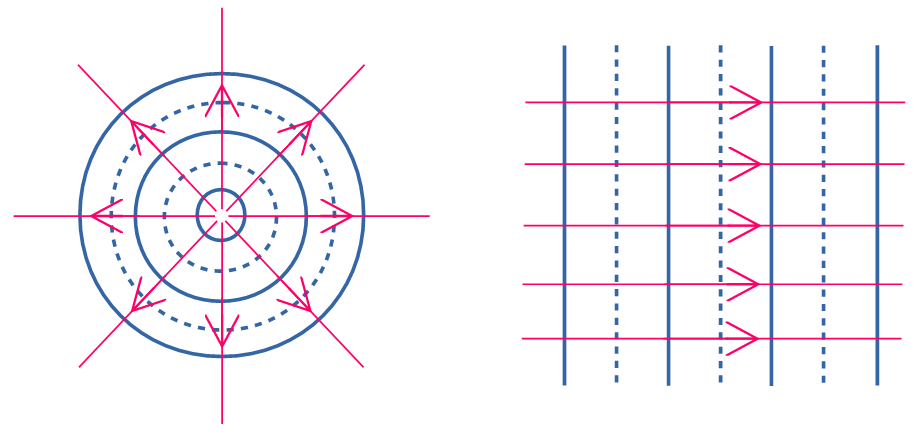
En una dimensión es más sencillo pues se trata de ver únicamente el sentido de propagación ya que la dirección es en la misma dimensión en la que se propaga la onda.

En el caso de tres dimensiones también se utilizan rayos, para el caso de una onda esférica la representación de los rayos que indican las direcciones y sentidos de propagación de los frentes de onda coincide con los radios de los círculos concéntricos al foco donde se genera la onda. Su representación sería como se ve en la siguiente figura:

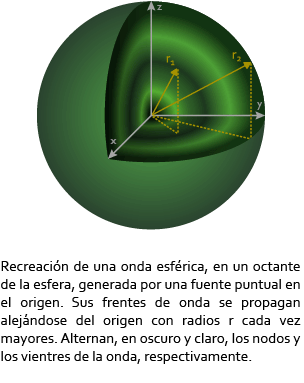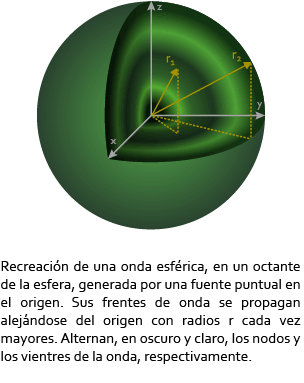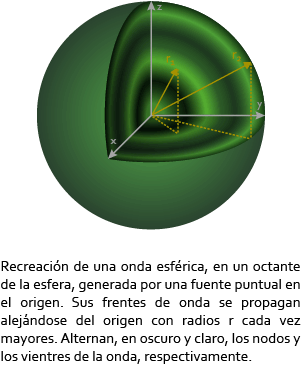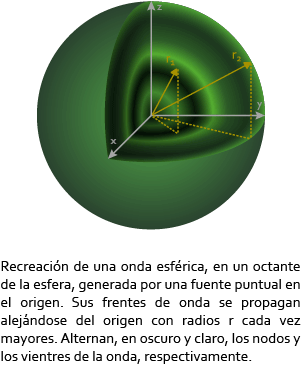
gif que muestra los frentes de onda y algunas direcciones y sentidos de propagación con el origen en el lugar donde se generan las ondas

4. Ondas periódicas

La clasificación de una onda como periódica refiere al tiempo entre las perturbaciones, es decir, una onda se llama periódica si el tiempo entre las perturbaciones es constante.

Estudiaremos el caso particular de las ondas periódicas armónicas, que son aquellas en las que el agente generador de la onda describe un movimiento armónico simple (M.A.S.). En el siguiente video se explica, para el caso de una onda periódica armónica que se desplaza por una cuerda, en qué consiste ese movimiento.

(Música del video: MixedSignals. Autor: Airtone. En dig.ccmixter.org/film. Licencia: CC BY-NC 3.0.)

No confundir la velocidad de la onda con la velocidad de las "porciones de cuerda". Como pudiste observar en el video, la onda se desplaza hacia la derecha, mientras que las "porciones de cuerda" se mueven hacia arriba y hacia abajo. Esto nos permite clasificar también a esta onda como transversal.

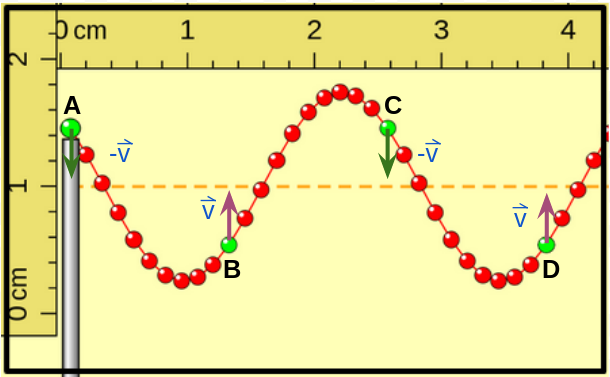
Analicemos cómo es la velocidad en algunas de las "porciones de cuerda" cuando la onda va pasando por ellas. Las siguientes imágenes muestran los vectores velocidad en diferentes posiciones del movimiento de una porción de la cuerda, míralas y lee detenidamente las aclaraciones.


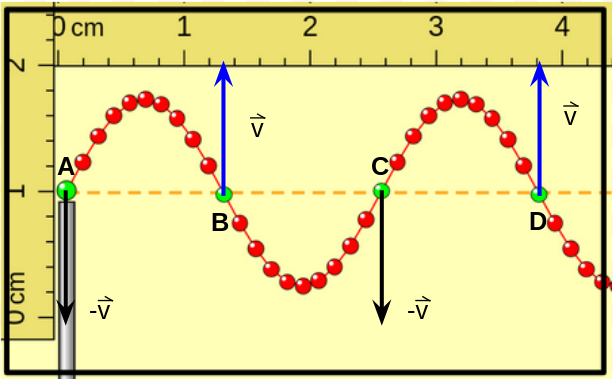
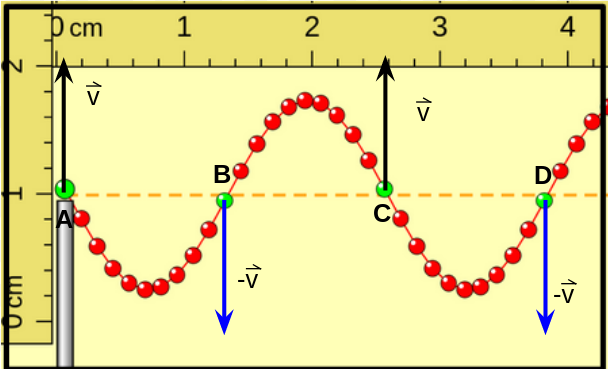
	En esta figura se representan las velocidades de las "porciones de cuerda" representadas con color verde cuando están pasando por la posición de equilibrio. Se marcaron con las letras A, B, C y D las cuatro porciones representadas con verde. Observar los círculos A y C tienen igual velocidad (igual módulo, dirección vertical y sentido hacia abajo) y que los puntos B y D también (igual módulo, dirección vertical y sentido hacia arriba).
	En esta imagen las porciones A, B, C y D se desplazaron de la posición de equilibrio. Observar que las velocidades de A y C tienen menor módulo pero dirección y sentido son iguales que en la imagen anterior. Lo análogo sucede con los punto B y D.
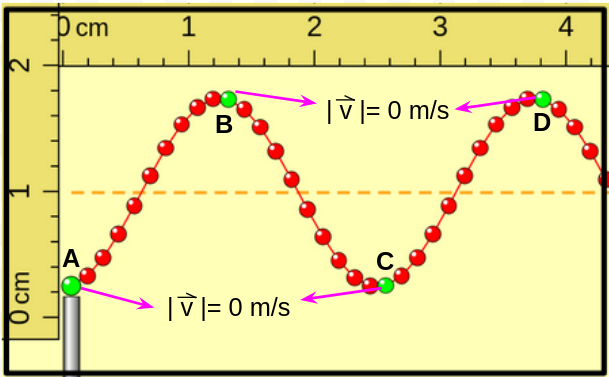
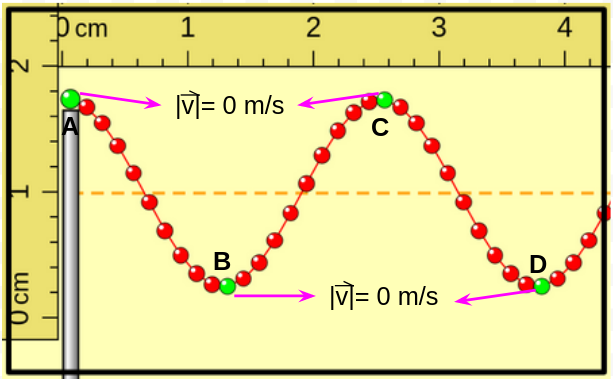
	Aquí las porciones A, B, C y D tienen la máxima separación de la posición de equilibrio, pero A y C se encuentran por debajo y B y D por encima. En este instante sus velocidades son nulas e inmediatamente después las porciones comienzan a moverse en sentido opuesto al que tenían antes de llegar a esta posición, como se muestra en la imagen a continuación.
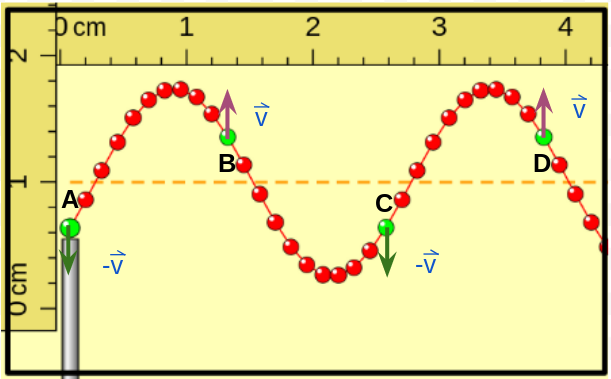
	La posición de las porciones indicadas ahora es por debajo de la posición de equilibrio, las velocidades de las porciones A y C son vertical hacia arriba y de igual valor y las de las porciones B y D son también de igual valor pero verticales hacia abajo.
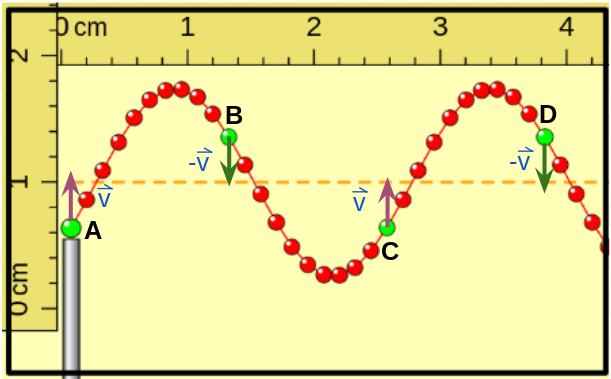
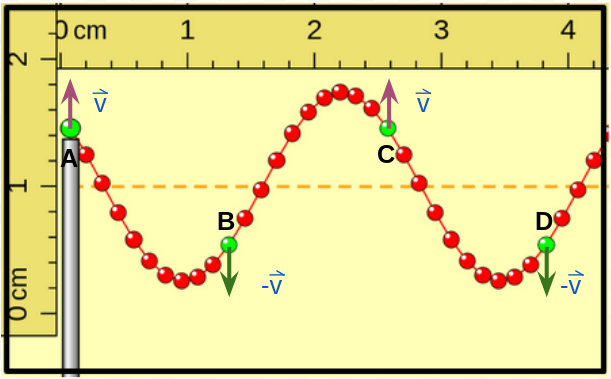
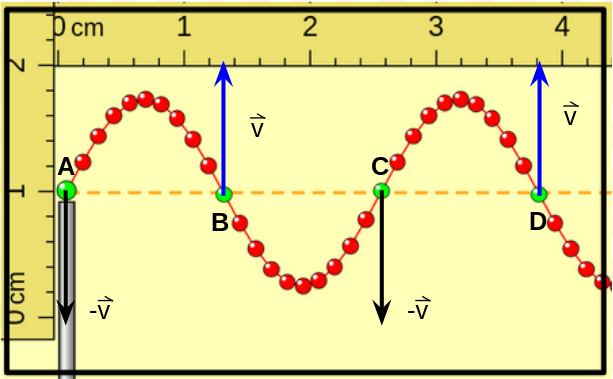
	En esta figura se representan las velocidades de las "porciones de cuerda" representadas con color verde cuando están nuevamente pasando por la posición de equilibrio. Las porciones A y C se mueven hacia arriba y las B y D hacia abajo.
	En esta imagen las porciones A, B, C y D se desplazaron de la posición de equilibrio, ahora A y C están por encima, pero B y D están por debajo. Observar que las velocidades de A y C tienen menor módulo pero dirección y sentido son iguales que en la imagen anterior. Lo análogo sucede con los punto B y D.
	Nuevamente las porciones A, B, C y D tienen la máxima separación de la posición de equilibrio, pero A y C se encuentran por encima y B y D por debajo. En este instante sus velocidades son nulas e inmediatamente después las porciones comienzan a moverse en sentido opuesto al que tenían antes de llegar a esta posición, como se muestra en la imagen a continuación.
	La posición de las porciones indicadas con A y C ahora es por encima de la posición de equilibrio, mientras que las indicadas con B y D por debajo, las velocidades de las porciones A y C son vertical hacia abajo y de igual valor y las de las porciones B y D son también de igual valor pero verticales hacia arriba. Un instante posterior se vuelve a obtener una imagen como la primera donde las porciones A, B, C y D alcanzan la posición de equilibrio con su velocidad máxima pero A y C se mueven hacia abajo y B y D se mueven hacia arriba, como se muestra a continuación, repitiéndose así todo el movimiento.
	Ídem a la imagen inicial.

La velocidad de las porciones de cuerda cambian con el tiempo, cuando una porción se encuentra en una cresta o en un valle su velocidad es cero, mientras que si se encuentra pasando por la posición de equilibrio de la cuerda su velocidad será máxima y su sentido será hacia arriba o hacia abajo.

Observación: el sentido de la velocidad de cada porción va a depender de cómo se encuentre ubicada la cuerda en el espacio, por ejemplo, si la cuerda se encuentra ubicada verticalmente, la dirección de la velocidad de cada porción de cuerda será horizontal y su sentido puede ser hacia la izquierda o hacia la derecha.

Las ondas periódicas pueden ser en uni, bi o tridimensionales.

Para simplificar su estudio, veremos sus características en una dimensión. Estas características también se aplican en dos y en tres dimensiones.

4.1. Magnitudes características de las ondas periódicas

Conjunto de Fichas creado con GoConqr por Silvia Pedreira

4.2. Representación de ondas periódicas en dos dimensiones

Supón que dejas gotear una canilla (de forma que las gotas caen a intervalos de tiempo constantes) sobre la superficie del agua tranquila que se encuentra en una pileta, tal cual se ve en el video que captura el simulador de la Universidad de Colorado Boulder.

Observa que se forman en la superficie del agua circunferencias concéntricas al lugar donde cae la gota. Las zonas más brillantes corresponden a las crestas de la onda y las zonas oscuras a los valles. La distancia entre dos zonas brillantes y dos zonas oscuras, corresponde a la longitud de la onda periódica que se está propagando por la superficie del agua.

Para representar ondas periódicas en dos dimensiones, por ejemplo en la superficie del agua.

5. Fenómenos ondulatorios en una y dos dimensiones

Mapa Mental creado con GoConqr por Silvia Pedreira

5.1. Reflexión de las ondas

Las ondas, ya sean unidimensionales, bidimensionales o tridimensionales se reflejan en mayor o menor medida al llegar a objetos. En situaciones cotidianas observamos la reflexión de las ondas, por ejemplo, el eco de un sonido emitido en una habitación grande y vacía o en un lugar abierto rodeado de superficies donde el sonido se puede reflejar. En los extremos de las cuerdas de una guitarra o de cualquier instrumento de cuerda, se reflejan los pulsos generados creando ondas que se llaman estacionarias (estas ondas estacionarias se estudian en cursos superiores). La reflexión de las ondas se aplica a diversos dispositivos tecnológicos, por ejemplo el sonar, algunas antenas de radio, entre otras y además los murciélagos, los delfines y otros animales utilizan este fenómeno para ubicarse y ubicar presas utilizando la ecolocalización.

Ondas unidimensionales

Extremo fijo

En la imagen se ve un pulso recorriendo la cuerda de un violín. Observa cómo al llegar a los extremos el pulso se refleja, y al hacerlo se invierte. ¿Por qué sucede esta inversión?

cuerda de violín en la que se observa la reflexión de un pulso

Observemos la inversión del pulso en el simulador de la Universidad de Colorado:

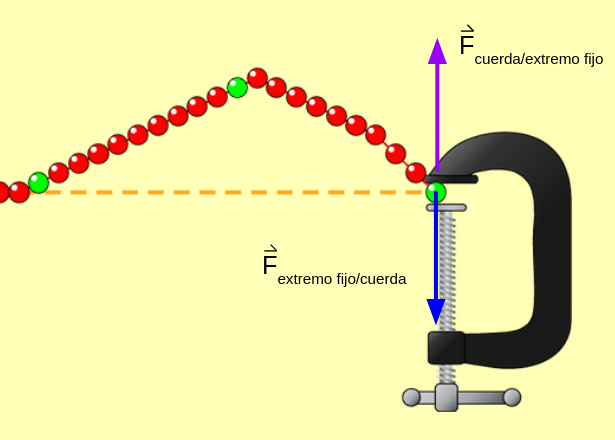
Esta inversión del pulso al llegar al extremo fijo se puede explicar con el Principio de acción y reacción, la cuerda le ejerce al extremo fijo una fuerza y el extremo fijo le ejerce a la cuerda otra fuerza con igual módulo y dirección pero con sentido opuesto, en la imagen a continuación puedes ver el diagrama de dichas fuerzas aplicadas sobre el extremo fijo (donde está atada la cuerda) y sobre la cuerda.

Captura de pantalla del simuador onda en una cuerda que muestra el instante en que el pulso llega al extremo fijo. Se han representado la fuerza que actúa sobre el extremo fijo y que realiza la cuerda, y la fuerza que actúa sobre la cuerda y que es ejercida por el extremo fijo.

Extremo libre

En el caso que el extremo de la cuerda sea libre, el pulso no se invierte, ya que el extremo no ejerce fuerza sobre la cuerda, por lo tanto la cuerda sube y baja sin experimentar inversión. En el video a continuación se muestra esta situación con el uso del simulador de onda en una cuerda.

Ondas bidimensionales

En la superficie del agua, si las ondas se encuentran con un obstáculo, también se pueden reflejar. Observa el siguiente video que te muestra cómo se reflejan las ondas en la superficie del agua.

Video: Experimento de ondas - Reflexión. Autor: Castillodelascs. Licencia Estándar de Youtube. Recuperado de: https://www.youtube.com/watch?v=nkInOdBAQpE

La reflexión de ondas planas en dos dimensiones se puede representar si se trata de un pulso:

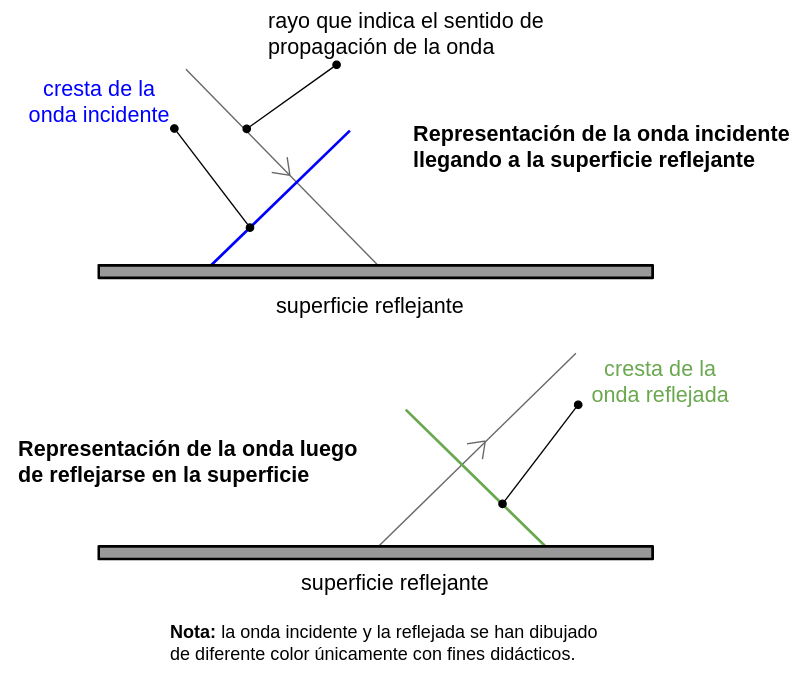
la imagen consta de dos partes, en la primera se muestra una onda que está llegando a una superficie reflejante, está representada con una línea recta de color azul y se indica que es la cresta de la onda incidente. Perpendicular a ella se muestra un rayo que indica el sentido de propagación de la onda. En la segunda parte se muestra la onda reflejada, representada con color verde, y perpendicular a ella se muestra el rayo que indica el sentido de propagación de esta onda reflejada.

Se puede representar esta misma situación mostrando el pulso incidente y reflejado en un mismo diagrama:

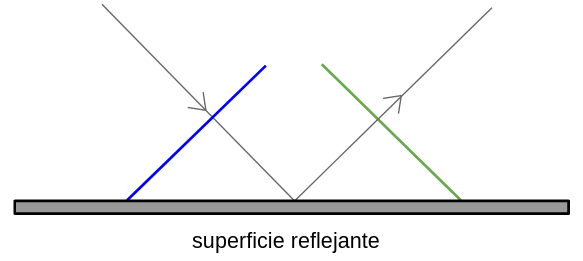
Se muestra el pulso u onda incidente representada con una línea de color azul llegando a la superficie reflejante y la onda reflejada que se ha representado con color verde, luego de un tiempo de ocurrida la reflexión.

La reflexión de ondas planas periódicas en dos dimensiones se puede representar:

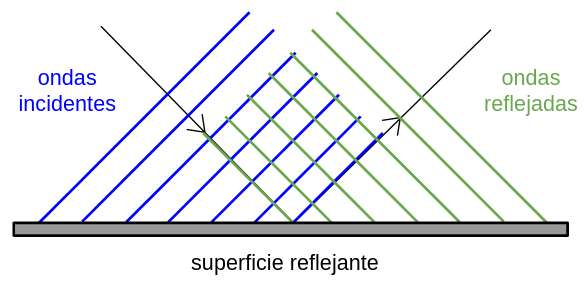
Se muestran ondas planas periódicas incidentes que van llegando a una superficie reflejante, representadas por líneas azules y paralelas y un rayo perpendicular a ellas que indica el sentido de propagación de las ondas. Se muestran también las ondas reflejadas, representadas por líneas verdes paralelas y el rayo que indica el sentido de propagación. La superficie reflejante está representada por un rectángulo de color gris con línea exterior negra.

En el caso de ondas periódicas con forma curva:

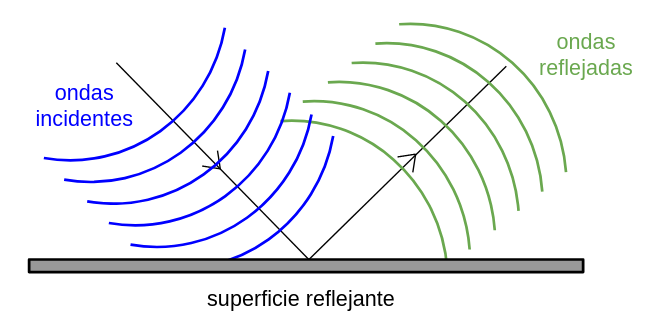
Se muestran frentes de onda periódicos y curvos que inciden el una superficie reflejante y los mismos frentes de onda un tiempo posterior reflejados.

5.2. Refracción de las ondas

Las ondas experimentan el fenómeno de la refracción de las ondas, cuando la onda que se propaga por un medio pasa a otro con diferentes características.

Al cambiar las características del medio la onda cambia su velocidad. A las ondas que cambian de medio se les llama ondas refractadas o transmitidas. Estudiaremos la refracción para las ondas unidimensionales y bidimensionales.

Refracción de ondas en una dimensión

Caso 1. El pulso es generado en la cuerda de menor densidad lineal de masa

En la imagen que se presenta a continuación se representaron dos cuerdas diferentes unidas. Las cuerdas tienen distinta densidad lineal de masa, como vimos anteriormente ésta es una propiedad característica de las cuerdas.

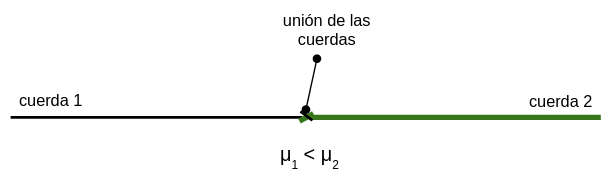
Si se genera un pulso en la cuerda 1 como se muestra en la figura:

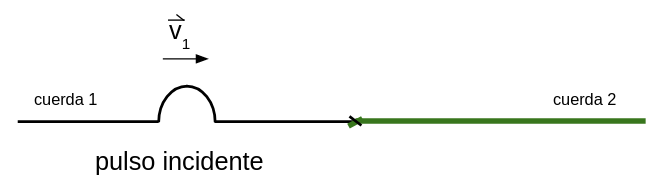
Se muestran dos cuerdas diferentes unidas, la cuerda de la izquierda de color negro y más fina que la otra se llama cuerda 1, en ella se ha generado un pulso que se mueve hacia la derecha con velocidad v1. El pulso se va aproximando a la unión de la cuerda 1 con la dos que es de color verde.

El pulso generado en la cuerda 1 se propaga hacia la derecha aproximándose a la unión con la cuerda 2. Momentos después de haber llegado a la unión se puede observar la situación que se representa:

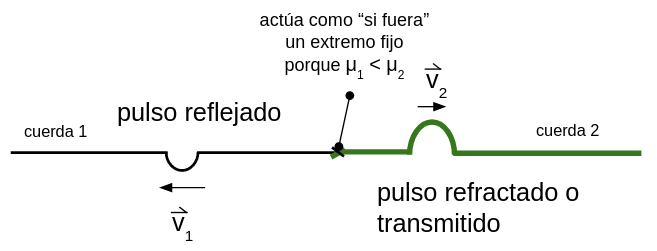
$se muestra en la cuerda de la izquierda el pulso reflejado que está por debajo de la posición de equilibrio de las cuerdas, en la cuerda verde de la izquierda se muestra el pulso refractado o transmitido que está por encima de la posición de equilibrio, se ha indicado que la velocidad de este pulso es v2, porque al cambiar de medio cambia su velocidad. También se muestra que el lugar de unión de las cuerdas actúa como "si fuera" un extremo fijo porque la densidad lineal de masa de la cuerda 1 es menor que la de la cuerda 2.$

El pulso reflejado en la cuerda 1 se invierte debido a que μ₁ < μ₂ , la unión de las cuerdas actúa como "si fuera" un extremo fijo, de esta forma la cuerda 2 le ejerce una fuerza a la cuerda 1 con sentido opuesto a la que la cuerda 1 le ejerce a la 2 y por eso el pulso reflejado se invierte. La velocidad del pulso transmitido o refractado disminuye porque la densidad lineal de masa de la cuerda 2 es mayor que la de la cuerda 1.

Caso 2. El pulso es generado en la cuerda de mayor densidad lineal de masa

Ahora el pulso es generado en la cuerda 2 y se propaga hacia la izquierda con velocidad 2:

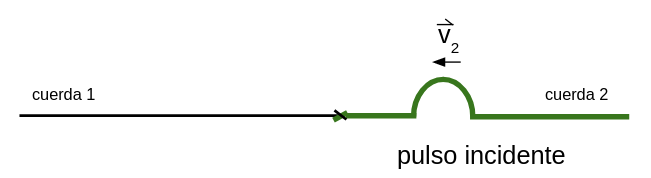
Se representan dos cuerdas unidas, la de la izquierda es negra y se llama cuerda 1, la de la derecha es verde y se llama cuerda 2. En la de la derecha se ha generado un pulso que se propaga hacia la izquierda con velocidad v2 y se le llama pulso incidente.

Momentos después de haber llegado a la unión se puede observar la situación que se representa:

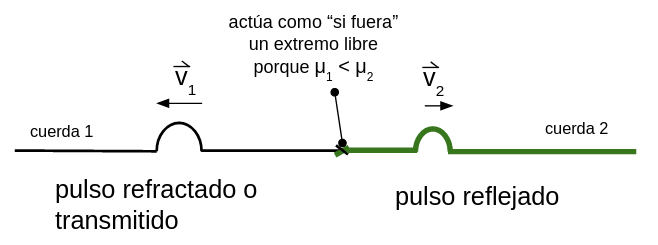
$Se muestran el pulso reflejado (que se mueve hacia la derecha con velocidad v2) en la cuerda verde de la derecha que no está invertido con respecto al pulso incidente, se explica que la unión de las cuerdas actúa como si fuera un extremo libre porque la densidad lineal de masa de la cuerda 1 es menor que la de la cuerda 2. En la cuerda 1 se muestra el pulso refractado o transmitido que se desplaza hacia la izquierda con velocidad v1..$

El pulso reflejado en la cuerda 2 no se invierte debido a que μ₁ < μ₂ , la unión de las cuerdas actúa como "si fuera" un extremo libre, de esta forma la cuerda 1, al ser de menor densidad lineal de masa que la cuerda 2, le ejerce una fuerza a la cuerda 2 que no logra la inversión del pulso que se refleja. Así vemos que actúa como "si fuera" un extremo libre, por eso el pulso reflejado no se invierte. La velocidad del pulso transmitido o refractado aumenta porque la densidad lineal de masa de la cuerda 1 es menor que la de la cuerda 2.

Refracción de ondas en dos dimensiones

Una onda que se propaga por la superficie del agua se refracta cuando el agua cambia la profundidad. El cambio de profundidad produce un cambio en las características del medio por el que se propaga la onda y hace que su velocidad se modifique. El video a continuación muestra, haciendo uso de la cubeta de ondas, todos los fenómenos que experimentan las ondas en la superficie del agua, se ha configurado para que el video comience en el tiempo 2:32, donde se observa la refracción de ondas periódicas en la superficie del agua hasta el tiempo 3:02.

Se puede esquematizar la refracción de las ondas periódicas en dos dimensiones como se ve en la figura a continuación:

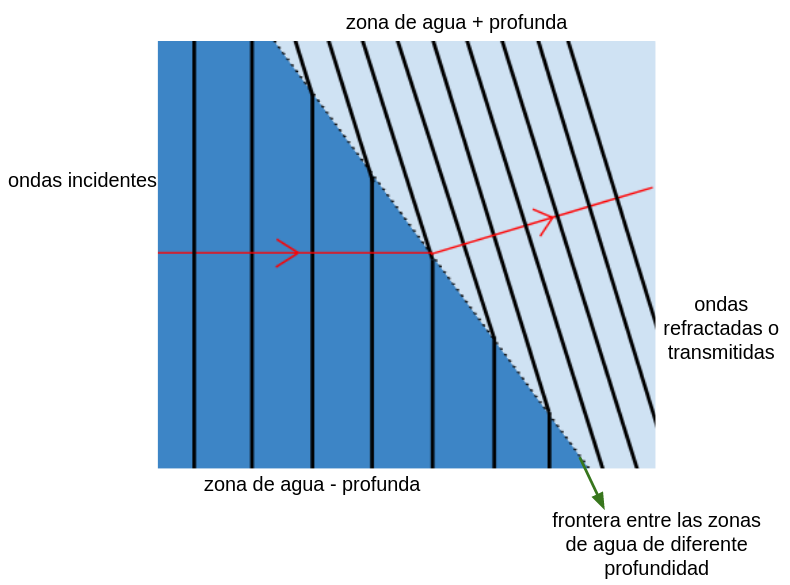
$La imaen muestra dos zonas, una de celeste oscuro (que representa la zona de agua más profunda) y otra de celeste claro (zona de agua menos profunda). En la zona de agua más profunda se muestran las ondas periódicas incidentes representadas por líneas paralelas verticales atravesadas perpendicularmente por un rayo de color rojo que indica la dirección y sentido de propagación de las ondas. La separación de las zonas está inclinada y en la zona de agua menos profunda se muestran las ondas refractadas o transmitidas, también paralelas entre sí pero con menor distancia entre las líneas, estas líneas también están atravesadas por un rayo de color rojo que indica la dirección y sentido de propagación.$

Si la frontera entre las zonas de diferente profundidad es paralela a las ondas planas periódicas el esquema sería:

se muestra el esquema de ondas planas periódicas propagándose por la superficie del agua. El agua presenta dos zonas una más profunda y otra menos profunda. En la más profunda las ondas están más separadas que en la otra.

En el simulador podrás visualizar los fenómenos de reflexión y refracción de ondas bidimensionales. Tienes que ir leyendo lo que está en el cuadro blanco a la derecha y abajo y luego ir haciendo clic en Siguiente paso. Prueba cambiando el ángulo de incidencia para ver los cambios.

5.3. Interferencia de ondas

Si dos o más ondas se propagan por el mismo medio y se encuentran en un lugar del espacio se van a superponer o a interferir.

El siguiente video hasta el minuto 3:06, muestra la interferencia de ondas en una dimensión. Luego sigue explicando las ondas estacionarias, ellas no se estudiarán en este curso.

Video: Superposición de ondas y ondas estacionarias. Autor: Dalton Avogadro. Licencia Estándar de Youtube. Recuperado de: https://www.youtube.com/watch?v=K6_INgXrkl8.

La interferencia de ondas se puede explicar por el Principio de superposición.

Principio de superposición de ondas, plantea que la onda resultante del encuentro entre ondas que se desplazan a la vez por el mismo medio equivale a la suma de cada una de las ondas por separado. Después de encontrarse e interferirse, cada una de las ondas mantiene su forma original.

Interferencia en una dimensión

En el gif a continuación puedes visualizar una representación de dos pulsos que viajan por una cuerda tensa, se ha indicado un punto en el lugar donde se va a producir la interferencia. A la izquierda de dicho punto la cuerda se muestra azul y a la derecha roja . En la imagen de arriba, el pulso que se desplaza hacia la derecha tiene amplitud positiva y el que viaja hacia la izquierda tiene amplitud negativa al encontrarse en el círculo negro se observa la interferencia, la suma de ambos pulsos visualizándose en determinado instante que la cuerda se encuentra horizontal. A este tipo de interferencia se le llama destructiva. Luego de producirse la interferencia cada uno de los pulsos sigue viajando con el sentido que tenía antes.

En la imagen de abajo, ambos pulsos tienen amplitud negativa, al encontrarse en el círculo negro se observa la interferencia, la suma de ambos pulsos visualizándose en determinado instante un pulso de amplitud máxima. A este tipo de interferencia se le llama constructiva. Luego de producirse la interferencia cada uno de los pulsos sigue viajando con el sentido que tenía antes.

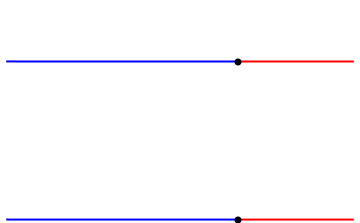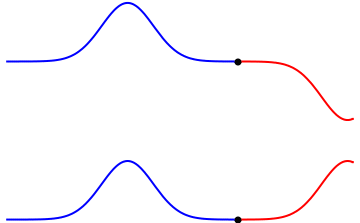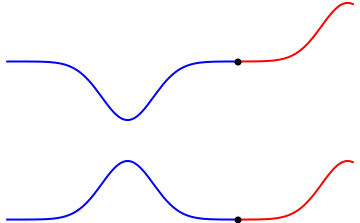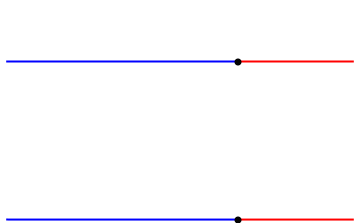
gif que muestra dos pulsos que viajan por una cuerda acercándose, en la imagen de arriba la interferencia es destructiva y en la de abajo constructiva.

Interferencia en dos dimensiones

El video a continuación muestra la interferencia en la superficie del agua de dos focos puntuales utilizando una cubeta de ondas:

Video: Cubeta de ondas, interferencia. Autor: Castillodelascs. Licencia Estándar de Youtube. Recuperado de: https://www.youtube.com/watch?v=ORgFE-QQM2w.

En la figura a continuación se ha tomado la imagen que se obtiene en la cubeta de ondas cuando se produce la interferencia de dos focos puntuales que vibran en fase. Se han llamado foco puntual 1 y 2 y se han representado las crestas de las ondas generadas por el foco 1 con color verde y las del foco 2 con rojo:

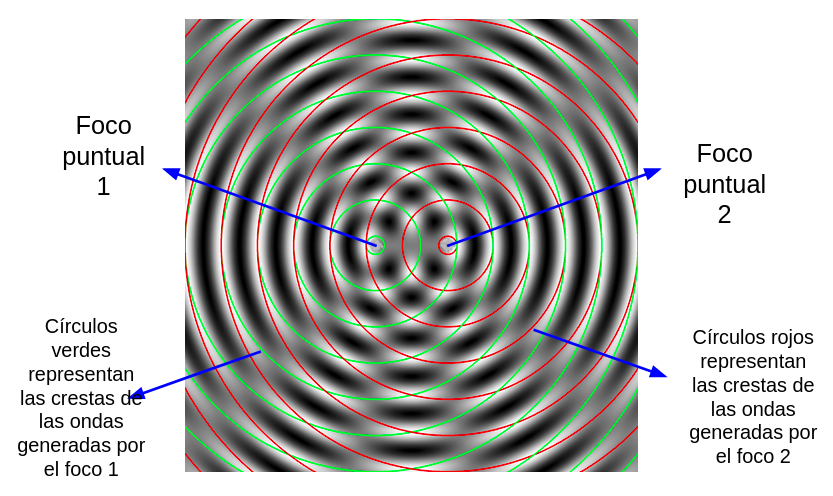
la figura muestra la imagen que se obtiene en la cubeta de ondas cuando se produce la interferencia de dos focos puntuales que vibran en fase. Se han llamado foco puntual al de la izquierda 1 y 2 al de la derecha y se han representado las crestas de las ondas generadas por el foco 1 con color verde y las del foco 2 con rojo.

En los lugares donde se cruzan dos crestas (una circunferencia verde y una roja) o dos valles (imagina circunferencias con línea punteada entre dos circunferencias con línea llena) se produce interferencia constructiva.

La figura que sigue muestra las zonas donde se produce interferencia constructiva (donde se cruzan dos crestas o dos valles):

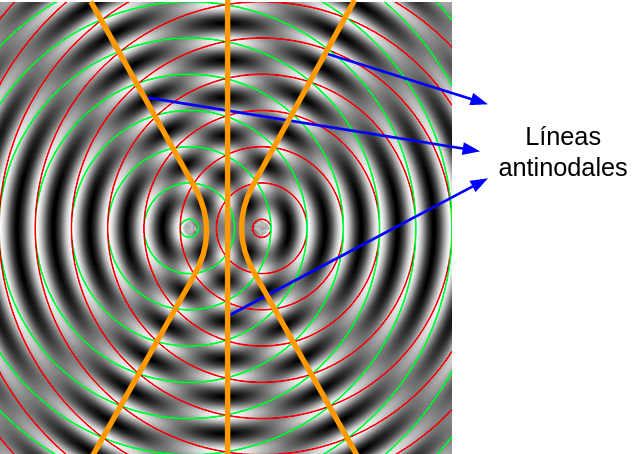
imagen que muestra las líneas antinodales o de interferencia constructiva, estas líneas surgen al unir las intersecciones de dos crestas y dos valles. Se muestra que las líneas pasan por las intersecciones de dos circunferencias una verde y la otra roja.

La siguiente figura muestra las zonas de interferencia destructiva que se encuentran intercaladas entre las zonas de interferencia constructiva. Estas líneas llamadas nodales surgen de la intersección de una cresta con un valle, piensa que muy similar a lo que ocurre en la cuerda del principio cuando uno de los pulsos viene por encima de la posición de equilibrio y se encuentra con otro que viene por debajo.

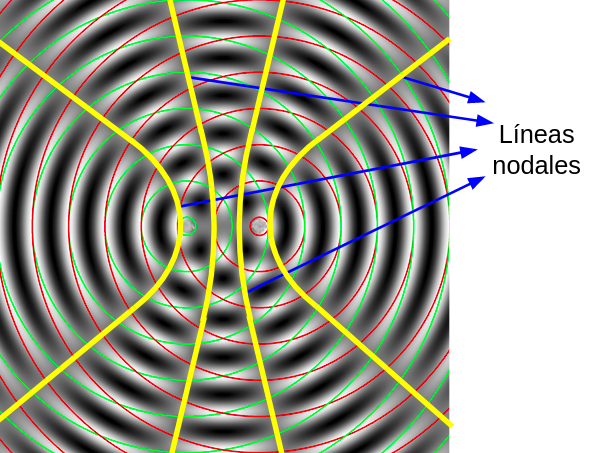
se muestra el diagrama de interferencia de dos focos puntuales en el que se han indicado con color amarillo las líneas nodales.

Ahora mostramos las líneas antinodales y nodales juntas en un mismo diagrama:

Se muestran las líneas nodales y antinodales juntas en el diagrama de interferencia de dos focos puntuales

En la interferencia de dos focos puntuales vibrando en fase, se pueden observar zonas de interferencia constructiva rodeadas de zonas de interferencia destructiva. Aquí en las líneas nodales el agua se encuentra en reposo en la posición de equilibrio. En las líneas antinodales la amplitud de las crestas y de los valles es el doble de la que tendrían si sólo hubiera un solo foco vibrando.

Dato: Las líneas nodales y antinodales tienen geometría hipérbólica.

5.4. Difracción de ondas

Alguna vez te preguntaste ¿cómo es posible que escuches cuando te llaman de la cocina si tu estás en el dormitorio?

La difracción de las ondas podría darte la respuesta. La difracción es un fenómeno por el cual las ondas son capaces de rodear los obstáculos que se interponen en su dirección de propagación.

Puede explicar también cómo las ondas del wifi llegan a todos los lugares de tu casa, estas ondas se reflejan en las paredes pero también se difractan si se encuentran con alguna abertura.

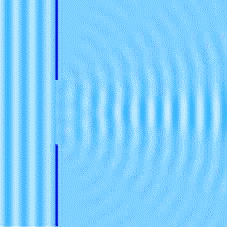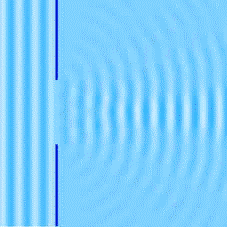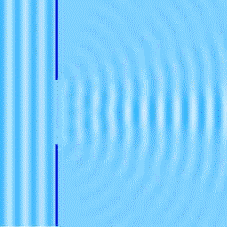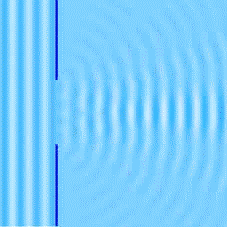
La difracción es un fenómeno característico de las ondas. La difracción de la luz, no se podía explicar con el modelo corpuscular. Este fenómeno no ocurre siempre, se tiene que cumplir la condición de que el tamaño del obstáculo o de la abertura sea parecido a la longitud de onda de la onda que se difracta. Si el tamaño de la abertura es muy grande comparado con la longitud de onda no se visualizará la difracción. Es por este motivo que en la historia de la ciencia se tardó tanto en encontrar que la luz también se difractaba. El tamaño de la abertura debe ser del orden de la longitud de onda de la luz para que se visualice su difracción (10^-7 m).

La imagen muestra ondas planas que llegan a un muelle y que al encontrarse con él se curvan (experimentan a difracción).

$Se muestra un muelle al que llegan ondas planas y al encontrarse con él se observa la difracción, es decir las ondas rodean el muelle.$

El siguiente video muestra la difracción de una onda bidimensional.

Video: Experimento de ondas. Autor: Castillodelascs. Licencia Estándar de Youtube. Recuperado de: https://www.youtube.com/watch?v=W1te-QiFXbs

La animación representa una onda plana propagándose por la superficie de un líquido y se encuentra con una abertura en la cual se difracta.

$animación que muestra una onda plana propagándose por la superficie de un líquido y se encuentra con una abertura en la cual se difracta.$

Los esquemas a continuación representan ondas planas que se propagan hacia una abertura (rendija) que va disminuyendo su tamaño. Observar que la onda rodea los obstáculos (se difracta) y se modifica la forma del frente de onda:

esquema que muestra líneas verticales separadas entre sí una misma distancia que representan las crestas de ondas periódicas. Estas ondas viajan hacia la derecha y en su camino se encuentran con dos obstáculos con forma rectangular (negros) cuya forma es paralela al frente de onda y su separación es mucho mayor que la longitud de onda. Luego de pasar por la abertura se ven las ondas paralelas entre sí sin cambiar su forma, sólo pasa la parte del frente de onda que tiene el tamaño de la abertura.

A medida que el tamaño de la abertura se acerca a la longitud de onda el cambio en el frente de onda se hace más notorio.

Pregunta:

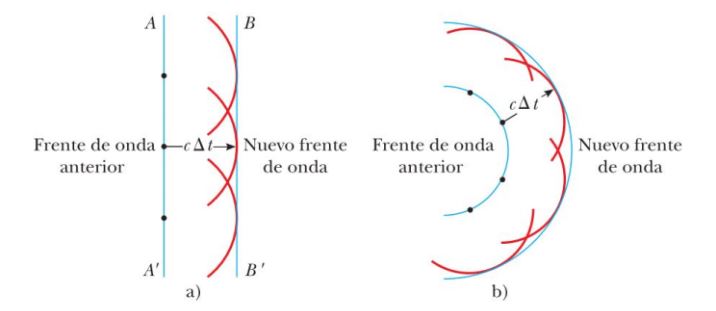
6. Principio de Huygens, para explicar la propagación de las ondas y los fenómenos

Cartel que muestra la frase: Todo punto de un frente de onda inicial puede considerarse como una fuente de ondas esféricas secundarias que se extienden en todas las direcciones con la misma velocidad, frecuencia y longitud de onda que el frente de onda del que proceden.

A continuación se muestra un esquema que describe el Principio de Huygens:

Se muestran dos esquemas a) y b). En el esquema a) en un frente de ondas plano, en la posición A' se indican tres puntos, en la posición B' esos tres puntos indicados en A' generaron ondas circulares que se propagaron y en la posición B' forman el nuevo frente de ondas plano. En el esquema b) ocurre lo mismo que en a) pero el frente de ondas ahora es circular y se han indicado 4 puntos.

7. Ondas Bidimensionales - Resumen de sus fenómenos

El video a continuación muestra todos los fenómenos vistos para las ondas en dos dimensiones, míralo con atención porque además servirá para repasar sobre las ondas periódicas.

Video: Experimentos con cubeta de ondas. Autor: Lavoisier2001. Licencia Estándar de Youtube. Recuperado de: https://www.youtube.com/watch?v=3-tymln0b1U.

8. Créditos

Bibliografía

Alvarenga, B. y Máximo, A. (1997). Física general. México: Oxford University.
Egaña, E; Berruti, M. y González, A. (2014). Interacciones 4. Campos y ondas. Uruguay: Contexto.
Hewitt, P. (2007). Física conceptual. México: Pearson-Addison Weasley.

Imágenes, sitios, simuladores y videos

Módulo de aprendizaje: Densidad de 1er año de Ciclo Básico. Autores: Gatto, A. y Pedreira, S. Portal Uruguay Educa. Recuperado de: http://aulas.uruguayeduca.edu.uy/course/view.php?id=218&section=12. Licencia: CC BY-SA 4.0.
Bowed violin string in slow motion.gif. Autor: ViolinB0W-Conundrumer. Licencia: CC BY 3.0.
Onda esférica 1.gif. Autor: Marta Moreno Miraballes. Licencia: CC BY-SA 4.0.
Interferencia de ondas: Reflection at fixed and free string ends single pulse.gif. Autor: Pieter Kuiper. Licencia: CC0 Dominio Público.
Principio de superposición de ondas. Wikipedia (2019).
Onda en una cuerda. PhET, Interactive simulations. Autores: Paul, A.; Dubson, M.; Olson, J.; Loeblein, P; Perkins, K.; Rouinfar, A.; Siman-Tov, S. Universidad de Colorado Boulder. Licencia: CC BY 4.0. Recuperado de: https://phet.colorado.edu/es/simulation/wave-on-a-string.
Reflexión y refracción de ondas. Explicación mediante el Principio de Huygens. Autor: Fendt, W. Licencia: CC BY-NC-SA 4.0.
Frente de onda: Raised fist.jpg. Autor: Tomas Funnarsson. Licencia: CC BY-SA 4.0
Frente de onda: Gotas cayendo en el agua. Autor desconocido. Licencia: CC0 Dominio Público.
Difracción de ondas: Muelle de madera, lago, agua, rocas, paisaje. Autor: En freejpg.com.ar. Licencia: CC BY 4.0.
Principio de Huygens: Energía de las ondas electromagnéticas 1. Autor: Experticius. Licencia: CC BY-SA 4.0.
Onda Periódica: Música del video: MixedSignals. Autor: Airtone. En dig.ccmixter.org/film. Licencia: CC BY-NC 3.0.
Video: Experimento de ondas - Reflexión. Autor: Castillodelascs. Licencia Estándar de Youtube. Recuperado de: https://www.youtube.com/watch?v=nkInOdBAQpE.
Video: Superposición de ondas y ondas estacionarias. Autor: Dalton Avogadro. Licencia Estándar de Youtube. Recuperado de: https://www.youtube.com/watch?v=K6_INgXrkl8.
Video: Experimento de ondas: Difracción. Autor: Castillodelascs. Licencia Estándar de Youtube. Recuperado de: https://www.youtube.com/watch?v=W1te-QiFXbs.
Video: Cubeta de ondas, interferencia. Autor: Castillodelascs. Licencia Estándar de Youtube. Recuperado de: https://www.youtube.com/watch?v=ORgFE-QQM2w.
Video: Experimentos con cubeta de ondas. Autor: Lavoisier2001. Licencia Estándar de Youtube. Recuperado de: https://www.youtube.com/watch?v=3-tymln0b1U.

Autoría del Módulo: Silvia Pedreira.

spedreira@uruguayeduca.edu.uy

Esta obra está bajo una Licencia Creative Commons Atribución 4.0 Internacional.

Portal Uruguay Educa

Febrero de 2019. Actualizado en Febrero 2022.