Carga eléctrica y campo electrostático

Sitio:	Aulas \| Uruguay Educa
Curso:	Física - 1º B.D.
Libro:	Carga eléctrica y campo electrostático
Imprimido por:	Invitado
Día:	martes, 7 de mayo de 2024, 03:59

Tabla de contenidos

1. Introducción
2. Electricidad estática
3. Modelo de Campo
- 3.1. Campo eléctrico
4. Líneas de campo eléctrico o líneas de fuerza
- 4.1. Características de las líneas de campo eléctrico
5. Interacción entre cuerpos cargados
6. ¿De qué variables depende la fuerza de interacción entre dos cuerpos cargados?
7. Balanza de Torsión - Ley de Coulomb
- 7.1. Simulador Ley de Coulomb
8. Autoevaluación
9. Determinación del campo eléctrico creado por una carga puntual
10. Superposición de campos eléctricos
11. Créditos

1. Introducción

El siguiente recurso trata sobre:

qué es la electrostática
qué es y dónde se encuentra la carga eléctrica
cuáles son las formas de transferencia de cargas eléctricas
cuáles son las características de la carga eléctrica

2. Electricidad estática

En el siguiente video de Micro Antel Ciencias explica a qué se deben fenómenos debidos al intercambio de cargas entre los cuerpos.

3. Modelo de Campo

En los capítulos anteriores se analizó que las cargas eléctricas interactúan sin la necesidad de estar en contacto. Se dice que la interacción entre cargas eléctricas es a distancia.

Para explicar las interacciones a distancia se crea el modelo de campo. En este modelo el campo es el intermediario entre los cuerpos, es el que informa al entorno de la presencia de un cuerpo con alguna propiedad.

Así, el entorno de un cuerpo sufre una "distorsión" si el mismo tiene masa, carga eléctrica o propiedades magnéticas.

Un cuerpo con masa, crea a su alrededor un Campo Gravitatorio, eso hace que otros cuerpos con la misma propiedad (masa) se vean atraídos a él.

Un cuerpo con carga eléctrica, genera a su alrededor un Campo Eléctrico, lo que provoca que otros cuerpos cargados positiva o negativamente se vean atraídos o repelidos.

Lo mismo sucede si el cuerpo tiene propiedades magnéticas, genera a su alrededor un Campo Magnético.

Estos campos mencionados son campos vectoriales, significa que a cada punto del espacio en el entorno de alguna de las propiedades mencionadas se le asigna un vector, con su módulo, dirección y sentido.

3.1. Campo eléctrico

El siguiente video de Antel Ciencias, se explica el concepto de campo eléctrico, también aclara de qué depende la interacción entre cargas eléctricas (Ley de Coulomb) e introduce la idea de las líneas de campo eléctrico o líneas de fuerza.

Si en un lugar del espacio se desea determinar si hay un campo eléctrico, generado por alguna carga o por un conjunto de cargas eléctricas, se tendría que ver si el espacio se encuentra "distorsionado". En ese lugar se podría colocar una carga de prueba (cuyo valor sea tan pequeño que no afecte el campo que se desea determinar). Si se observa que la carga de prueba experimenta una fuerza de origen eléctrico, significa que en ese lugar hay un campo eléctrico, cuyas características se podrían determinar, como:

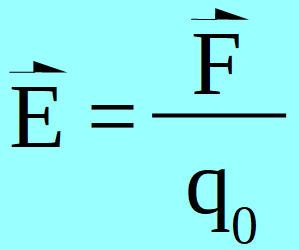
ecuación de campo eléctrico: el vector campo eléctrico es igual al cociente del vector fuerza eléctrica que actúa sobre la carga de prueba, dividido el valor de la carga de prueba.

Siendo , el vector campo eléctrico, la fuerza que actúa sobre la carga de prueba y q₀ el valor de la carga de prueba.

La unidad del vector campo eléctrico surge de la propia expresión: N/C (unidad de fuerza Newton dividido la unidad de carga eléctrica Coulomb).

Representación del campo eléctrico en el lugar donde colocamos una carga de prueba positiva:

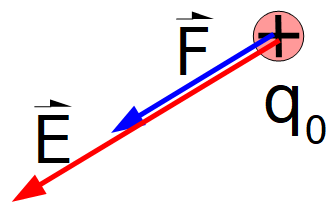
carga de prueba positiva sobre la cual actúa una fuerza eléctrica, también está representado el vector campo eléctrico, el mismo tiene igual dirección y sentido que la fuerza eléctrica.

Si se coloca una carga de prueba negativa, en el mismo lugar que se había colocado la carga positiva, la representación del campo eléctrico en dicho lugar es la que muestra la figura de abajo, observar que el vector campo eléctrico no se ve modificado, aunque si cambie la fuerza eléctrica sobre la carga de prueba:

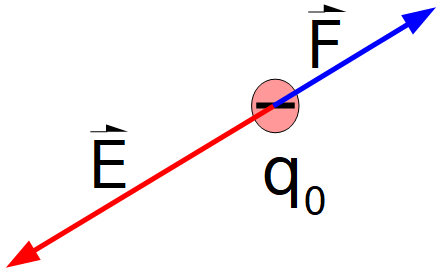
carga de prueba negativa sobre la cual actúa una fuerza eléctrica, también está representado el vector campo eléctrico, el mismo tiene igual dirección, pero sentido opuesto al de la fuerza eléctrica.

Por convención, la carga de prueba se elige positiva, de ese modo en cada punto el vector campo eléctrico tiene igual dirección y sentido que la fuerza eléctrica que actúa sobre la carga de prueba.

En el siguiente video se puede observar cómo se modifica la fuerza que actúa sobre la carga de prueba (recordar que es positiva por convención) al moverla en las proximidades de otra carga (la carga que crea un campo eléctrico a su alrededor es llamada carga fuente). También se observa cómo cambia la situación si son dos cargas de igual signo o de diferente signo, por ejemplo.

A partir del minuto 1:03, se puede visualizar que la representación del vector campo eléctrico no depende de la presencia de la carga de prueba. El campo eléctrico existe en el espacio que rodea a un cuerpo cargado, la carga de prueba se usa como detector, pero si se saca el detector, el campo eléctrico no se modifica en ese lugar. La ecuación que aparece en el minuto 1:50, es la suma de todas las fuerzas que actúan sobre la carga de prueba, aplicando la Ley de Coulomb entre la carga de prueba y cada una de las demás cargas de la distribución, el símbolo que aparece a la derecha de la ecuación

, es el vector unitario (que se estudiará en cursos superiores). En definitiva lo que se obtiene es la misma ecuación vista más arriba, despejada:

Aclaración: la última expresión matemática que aparece en el video para el campo eléctrico solamente es válida si la distribución de cargas está formada por cargas puntuales.

Video: Campo eléctrico. Autor: Pepenjuto. Licencia Estándar de YouTube. Recuperado de: https://www.youtube.com/watch?v=6UKxj7cba68.

4. Líneas de campo eléctrico o líneas de fuerza

Las líneas de campo eléctrico son una forma de representar el Campo Eléctrico en las proximidades de diferentes distribuciones de carga eléctrica.

En la imagen se representan las líneas de campo eléctrico en las proximidades de dos cargas puntuales (dos positivas primero y luego una positiva y una negativa), se observan los vectores campo eléctrico resultante creado por ambas cargas en los puntos A, B y C. Este vector campo resultante es tangente a las líneas de campo en cada punto:

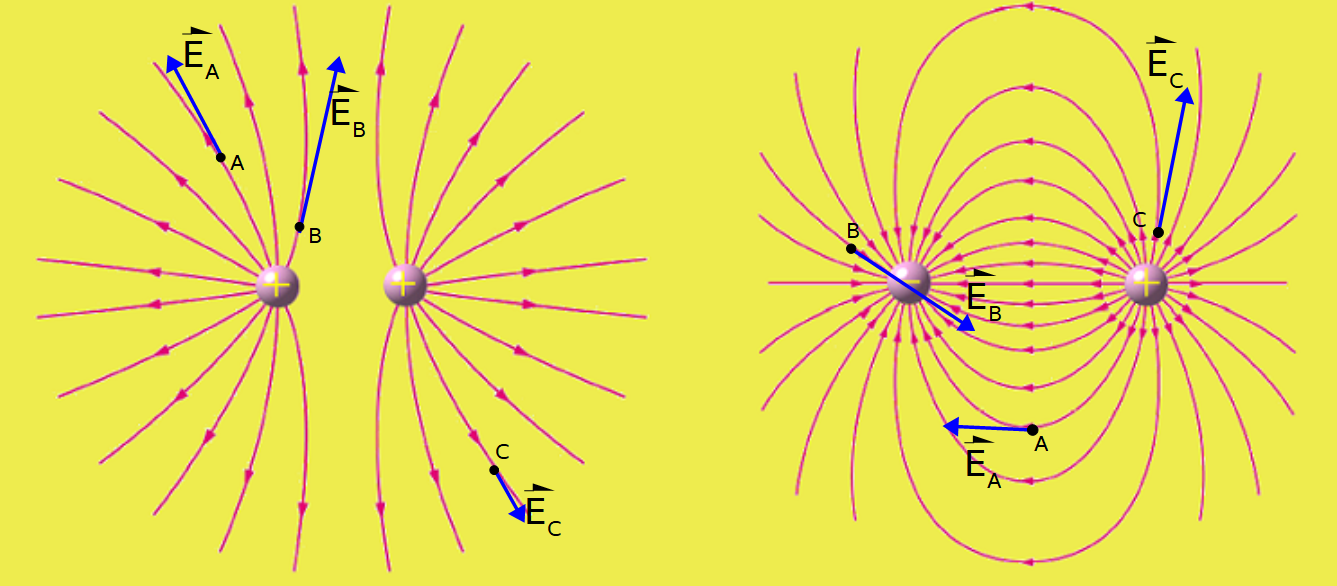
Distribución de líneas de campo eléctrico entre dos cargas positivas y entre dos cargas de distinto signo, tangente a algunas líneas se representaron los vectores campo eléctrico en varios puntos.

Imagen: Líneas de campo eléctrico.png. Autor: Chanchocan, Wikimedia. Licencia: CC BY-SA 3.0.

4.1. Características de las líneas de campo eléctrico

Como habrás visto en los simuladores anteriores, las líneas de campo eléctrico son curvas imaginarias que ayudan a representar el campo eléctrico en el entorno de una distribución de cargas. Estas líneas tienen las siguientes características:

Su sentido es entrante a los cuerpos cargados negativamente y saliente de los cuerpos cargados positivamente.

Líneas de campo de un cuerpo cargado negativamente, se muestra que son entrantes al cuerpo. A la derecha otra imagen que muestra las líneas de campo de un cuerpo puntual cargado positivamente, las líneas en este caso son salientes del cuerpo.

El vector campo eléctrico es tangente a las líneas de campo en cualquier punto de dicha línea.
Si las líneas de campo están más juntas el campo eléctrico es de mayor valor que si las líneas se encuentran más separadas. El módulo del vector campo eléctrico es proporcional a la densidad de líneas de campo en la región donde se está representando el vector campo.

Imagen que muestra el vector campo eléctrico en varios puntos, su dirección es tangente a las líneas de campo y su módulo (tamaño) es mayor o menor según las líneas de campo estén más juntas o más separadas respectivamente.

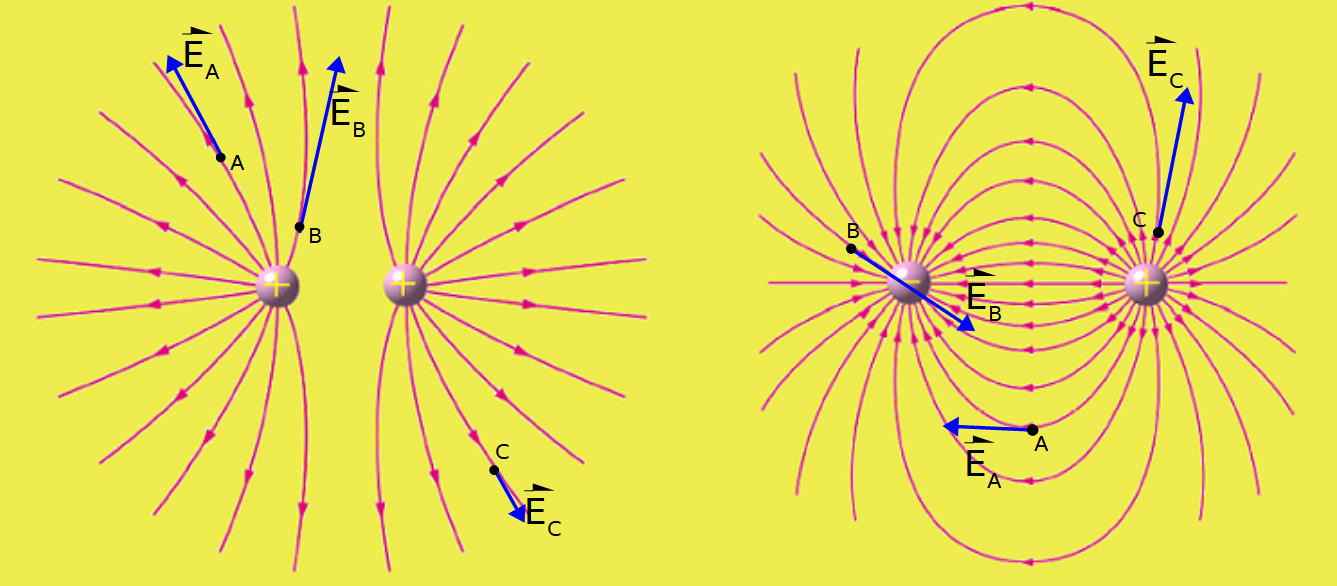
La cantidad de líneas de campo es proporcional al valor de la carga del cuerpo. Así, como se ve en la figura de abajo, del cuerpo cargado positivamente tiene el doble de valor de carga que el que está cargado negativamente. Del cuerpo cargado positivamente salen 16 líneas de campo, pero en el cargado negativamente sólo entran 8 porque su valor de carga es la mitad. En un esquema, podremos saber que un cuerpo tiene mayor valor de carga que otro, si de él salen o entran mayor cantidad de líneas de campo eléctrico.

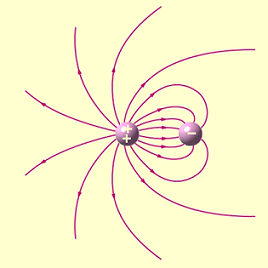
La imagen muestra dos cargas una positiva y otra negativa de distinto valor, de la carga positiva salen 16 líneas de campo y en la negativa entran sólo 8 pues el valor de la positiva es el doble de la negativa en valor absoluto.

Las líneas de campo eléctrico no se cortan, en cada punto del espacio solo puede haber una línea de campo.

Imágenes:

Líneas de campo eléctrico.png. Autor: Chanchocan, Wikimedia. Licencia: CC BY-SA 3.0.

Campo de cargas diferentes.png. Autor: Chanchocan, Wikimedia. Licencia: CC BY-SA 3.0.

Líneas de campo.svg. Autor: Jfmelero, Wikimedia. Licencia: CC BY-SA 3.0.

5. Interacción entre cuerpos cargados

Observa el siguiente video del Prof. Ignacio Correa:

Identifica en él los momentos en los que se produce alguna transferencia de cargas eléctricas.
Identifica los momentos en que los cuerpos se atraen o se repelen y piensa una explicación.
Realiza un diagrama explicativo de la situación.

Créditos del video: Correa, I. (2011). Carga eléctrica. Recuperado de: https://www.youtube.com/watch?v=_9uajkA_CYc. Licencia Estándar de YouTube.

6. ¿De qué variables depende la fuerza de interacción entre dos cuerpos cargados?

Con la ayuda de un simulador se analizará de qué factores depende la fuerza de interacción entre cuerpos cargados.

Utilizando el simulador realiza las acciones detalladas más abajo:

Primera parte:

Observa que todos los objetos (buzo de lana, globo y muro) tienen igual cantidad de cargas positivas y negativas.
Elimina el muro, por ahora sólo estudiarás la interacción entre el globo y el buzo.
Arrastra el globo y frótalo sólo con la manga del buzo. Trata que sólo sean removidas hacia el globo las cargas negativas de la manga.
Mueve el globo lo más a la derecha posible y suéltalo. Observa y toma nota de cómo se mueve.
Reinicia el globo y frótalo con toda la superficie del buzo, de forma que todas las cargas negativas del buzo sean transferidas al globo.
Repite el paso 4.

¿Cuál es la variable que modificaste? (variable independiente)

¿Cuál fue la variable que permaneció constante? (variable de control)

¿Qué variable mediste? (variable dependiente)

Realiza una descripción de lo observado en los pasos 4 y 6. Luego elabora una explicación teniendo en cuenta cómo cambió la variable dependiente cuando modificaste la variable independiente.

Segunda parte:

Observa que todos los objetos (buzo de lana, globo y muro) tienen igual cantidad de cargas positivas y negativas.
Elimina el muro, por ahora sólo estudiarás la interacción entre el globo y el buzo.
Arrastra el globo y frótalo con toda la superficie del buzo, de forma que todas las cargas negativas del buzo sean transferidas al globo.
Mueve el globo lo más a la derecha posible y suéltalo. Observa y toma nota de cómo se mueve cuando se desplaza una distancia de 2 cm.
Con el globlo igual que en el punto 3, suéltalo de una distancia a 2 cm de la manga del buzo. Observa y toma nota de cómo se mueve cuando está más cerca del buzo.

¿Cuál es la variable que modificaste? (variable independiente)

¿Cuál fue la variable que permaneció constante? (variable de control)

¿Qué variable mediste? (variable dependiente)

Realiza una descripción de lo observado en los pasos 4 y 5. Luego elabora una explicación teniendo en cuenta cómo cambió la variable dependiente cuando modificaste la variable independiente.

7. Balanza de Torsión - Ley de Coulomb

La balanza de torsión fue creada por Charles Coulomb en 1777, con el fin de medir la fuerza electrostática entre dos cargas. El dispositivo consiste en dos bolas de metal sujetas por los dos extremos de una barra suspendida por un cable o filamento. En la imagen se ven las partes que la forman:

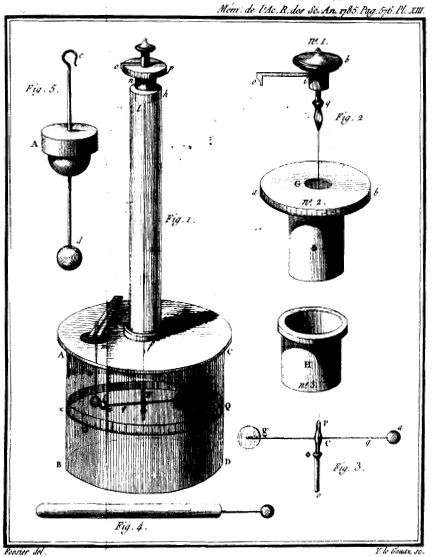
partes de la balanza de torsión de Coulomb

Para medir la fuerza electrostática se acerca una tercera bola cargada a una cierta distancia. Las bolas se atraerán o se repelerán, haciendo que la barra rote un cierto ángulo, así se puede determinar la fuerza medida en Newtons que se necesita para torsionar la balanza un ángulo conocido. Con la balanza de torsión Coulomb logró medir la fuerza de atracción o repulsión que se ejercen cuerpos cargados, llegando en 1785 a la relación matemática conocida como Ley de Coulomb, la que plantea que la fuerza de interacción eléctrica entre dos cargas es directamente proporcional al producto de las cargas e inversamente proporcional al cuadrado de la distancia que las separa.

Si se considera el sistema formado por dos cargas eléctricas en reposo, separadas una distancia d, como muestra la figura:

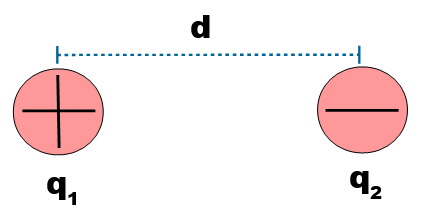
una carga q1 positiva separada una distancia d, de una carga q2 negativa

La representación de la fuerza de interacción entre ellas es:

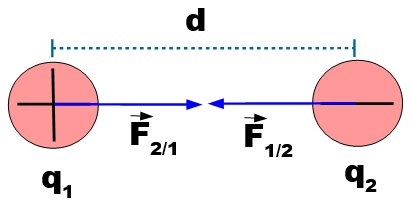
una carga q1 positiva separada una distancia d, de una carga q2 negativa, sobre cada una de las cargas está representada la fuerza de interacción

La fuerza de interacción se determina con la siguiente ecuación, conocida como Ley de Coulomb:

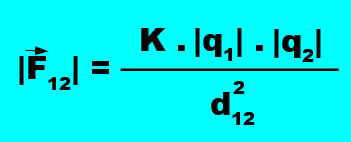
fuerza de la carga uno sobre la dos es igual a una constante por el producto del valor absoluto de las cargas dividido entre el cuadrado de la distancia que separa dichas cargas.

Siendo:

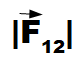es la fuerza de atracción entre las cargas eléctricas
|q₁| y |q₂| es el valor absoluto de las cargas.
d₁₂ es la distancia que separa dichas cargas.
K es la constante de Coulomb, esta constante de proporcionalidad depende de la constante dieléctrica y de la permitividad del material que rodea a las cargas. Cuando las cargas se encuentran en el vacío el valor de K = 9,0 x 10⁹ N.m²/C²

7.1. Simulador Ley de Coulomb

En el siguiente simulador podrás visualizar lo tratado anteriormente. Para usarlo debes permitir que se active algún visualizador Flash.

Guía de trabajo con el simulador:

Fija los valores de las cargas (cuadros de abajo a la izquierda) en 2 y -2 µC (ten en cuenta que µC es un submúltiplo del Coulomb que significa que 1 µC es 1 x 10^-6 C).
Arrastra una de las cargas de modo que la distancia entre ellas sea de1,0 cm.
Determina el valor de la fuerza entre las cargas en estas condiciones utilizando la Ley de Coulomb y compáralo con el valor que te brinda el simulador. Al aplicar la Ley de Coulomb, ten en cuenta que los valores de las cargas deben estar en Coulomb y la distancia entre ellas en metros.
Duplica el valor de la distancia y observa cómo se modifica el módulo de la fuerza. ¿Cuántas veces disminuye el valor de la fuerza?
Vuelve a la distancia entre las cargas de 1,0 cm y duplica el valor de una de las cargas. Observa cómo se modifica el módulo de la fuerza. ¿Cuántas veces aumenta el valor de la fuerza?
Realiza otros cambios que te parezcan interesantes de estudiar y anota los resultados que obtuviste.

Créditos del simulador:

Ley de Coulomb. Autor: Jesús Peñas. Licencia: Educaplus.

8. Autoevaluación

Realiza el siguiente cuestionario para autoevaluarte sobre lo visto hasta ahora:

9. Determinación del campo eléctrico creado por una carga puntual

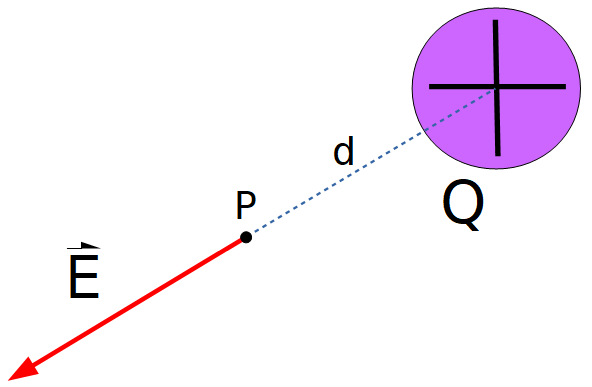
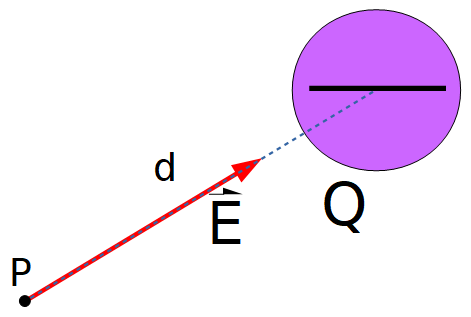
Para determinar el campo eléctrico en el entorno de una carga puntual, se utilizará el concepto de campo eléctrico y la Ley de Coulomb.

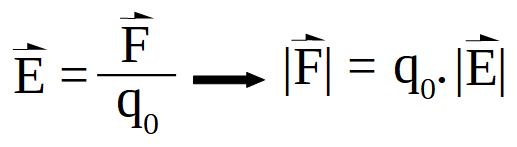
ecuación de campo eléctrico: el vector campo eléctrico es igual al cociente del vector fuerza eléctrica que actúa sobre la carga de prueba, dividido el valor de la carga de prueba.

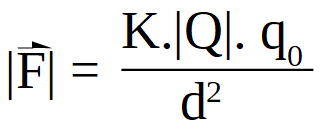
ecuación Ley de Coulomb, la fuerza de interacción entre la carga fuente y la carga de prueba en un punto P,es igual a la constante de Coulomb multiplicada por el valor absoluto del valor de la carga fuente por la carga de prueba, dividido entre la distancia al cuadrado.

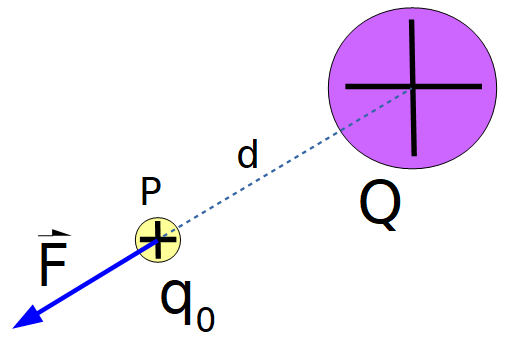
Esquema que muestra una carga fuente Q, a una distancia d de ella se encuentra una carga de prueba q sub cero, sobre la que se ha representado la fuerza que le ejerce la carga fuente Q.

Siendo:

Q la carga fuente (carga que crea campo eléctrico a su alrededor, que modifica su entorno).
q₀ es la carga de prueba o carga testigo, que se usa como "detector" de campo eléctrico y está ubicada en un punto P a una distancia d de la carga Q.
Sobre la carga de prueba q₀ , se ha representado la fuerza que le ejerce la carga fuente Q en dicho punto.

Al sustituir la fuerza en la ecuación de la ley de Coulomb por el producto de q₀ por el módulo de campo eléctrico:

Se puede simplificar q₀, que multiplica ambos miembros de la ecuación:

Por lo tanto el módulo del campo eléctrico creado por una carga puntual Q se puede determinar con la siguiente ecuación:

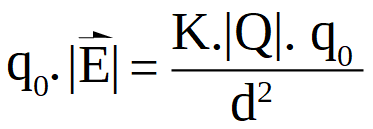
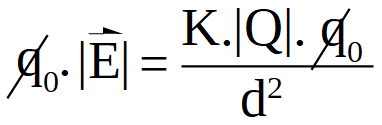
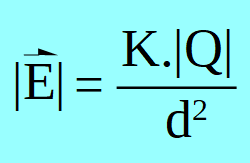
El módulo del campo eléctrico de una carga puntual es igual a la constante de Coulomb por el valor absoluto de la carga dividido el cuadrado de la distancia desde la carga Q hasta el lugar donde se desea determinar el campo eléctrico.

La representación del vector campo eléctrico para este ejemplo es:

Esquema que muestra una carga fuente Q, a una distancia d de ella se encuentra el punto P donde se ha representado el vector campo eléctrico.

De esta forma se puede determinar el campo eléctrico en la región que rodea a una carga puntual.

En el caso que la carga fuente sea negativa, el módulo se determina con la misma ecuación que para la positiva, pero la representación cambia a:

Esquema que muestra una carga fuente Q negativa, a una distancia d de ella se encuentra el punto P donde se ha representado el vector campo eléctrico, la dirección de dicho vector se encuentra en la recta que une el punto P con la carga y el sentido es hacia la carga..

10. Superposición de campos eléctricos

Cuando en una región del espacio se encuentran presentes varios cuerpos cargados, el campo en cada punto será el que resulte de la suma de cada uno de los campos creados por cada carga en un punto determinado.

Se analizarán 3 casos:

Caso 1: Campos eléctricos colineales y de igual sentido

Caso 2: Campos eléctricos colineales y de sentido opuesto.

Caso 3: Campos eléctricos no colineales.

10.1. Caso 1: Campos eléctricos colineales y de igual sentido

Supón la siguiente distribución de cuerpos cargados eléctricamente:

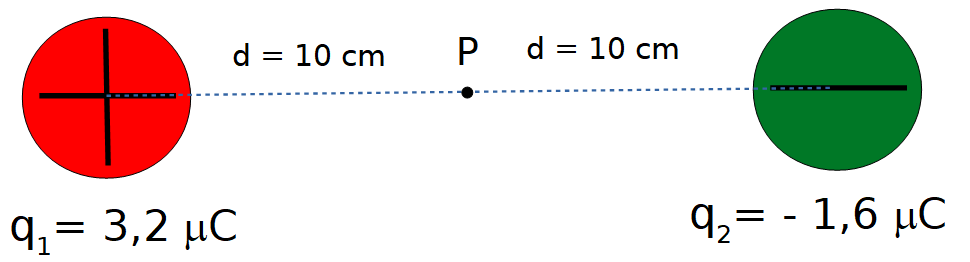
dos cuerpos cargados, uno positiva (de valor 3,2 micro Coulomb) y otro negativamente (de valor 1,6 micro Coulomb), separados una distancia de 20 cm, en el centro de la distancia entre los cuerpos se ubica un punto P.

Se desea determinar el valor del campo eléctrico en el punto P.

Para ello se determinará el campo eléctrico creado por la carga 1 en el punto P utilizando la ecuación de campo eléctrico de una carga puntual.

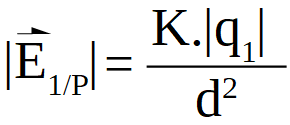
Ecuación campo eléctrico creado por el cuerpo cargado 1 en el punto P es igual a la constante de Coulomb por la carga del cuerpo 1 dividido entre el cuadrado de la distancia entre el cuerpo cargado y el punto P.

Se sutituyen los valores en la ecuación teniendo en cuenta que las magnitudes deben tener las mismas unidades que las de la constante de Coulomb, es decir, la carga eléctrica debe tiene que estar en Coulomb y la distancia en metros

1μC es igual a 1x10^-6 C

100 cm es igual a 1 m

Por tanto:

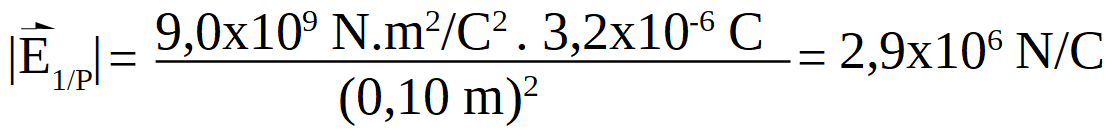
sustitución en la ecuación de campo creado por el cuerpo cargado 1, es igual a 9,0 por 10 a la nueve por 3,2 por diez a la menos 6 dividido entre 0,10 al cuadrado, esa operación es igual a 2,9 por diez a la 6 Newton/Coulomb

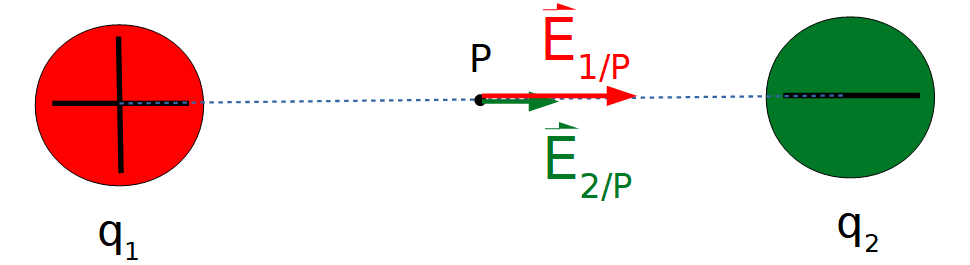
Se representa dicho vector en el punto P

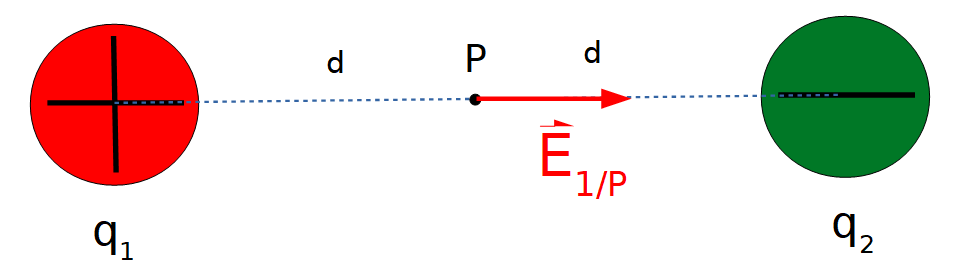
Esquema de la representación del vector campo eléctrico creado por el cuerpo cargado 1 en el punto P, el mismo tiene dirección horizontal y sentido hacia la derecha porque la carga es positiva y el punto está ubicado a la derecha del cuerpo.

Se determina ahora el valor del campo eléctrico creado por el cuerpo cargado 2:

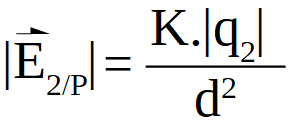
campo eléctrico creado por el cuerpo cargado 2 en el punto P es igual a la constante de Coulomb por el valor de la carga del cuerpo 2 dividido el cuadrado de la distancia entre el cuerpo y el punto P.

al sustituir los valores:

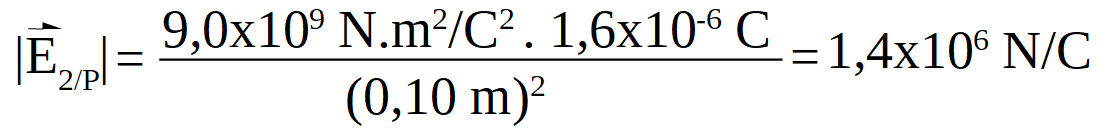
el módulo del campo eléctrico creado por el cuerpo 2 en el punto P, es igual a 9,0 por 10 a la 9 por 1,6 por diez a la -6 dividido entre 0,10 al cuadrado, eso es igual a 1,4 por diez a la 6 Newton/Coulomb.

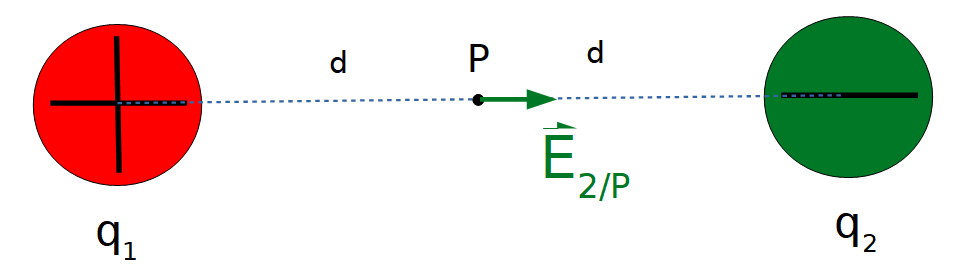
Se representa ahora dicho vector campo eléctrico en el punto P:

Esquema de la representación del vector campo eléctrico creado por el cuerpo cargado 2 en el punto P, el mismo tiene dirección horizontal y sentido hacia la derecha porque la carga es negativa y el punto está ubicado a la izquierda del cuerpo.

En los esquemas anteriores se representaron los vectores campo eléctrico creados por cada carga en el punto P, de forma independiente. Para mostrar que en el punto P influyen los campos creados por las dos cargas, la representación de los dos a la vez:

Esquema de la representación del vector campo eléctrico creado por los cuerpo cargado 1 y 2 en el punto P, ambos tienen igual dirección y sentido, horizontal a la derecha, pero uno es el doble de valor que el otro.

Debido a que ambos vectores tienen igual dirección y sentido, los módulos de los campos se suman y el campo eléctrico resultante en el punto P es:

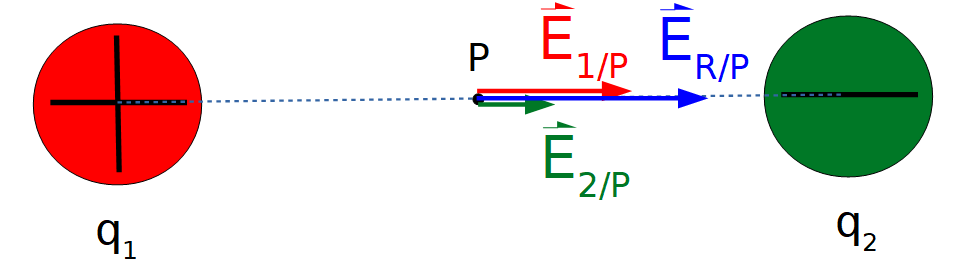
Esquema de la representación del vector campo eléctrico resultante en el punto P, creado por los cuerpos 1 y 2. Su dirección es horizontal y su sentido hacia la derecha. En el esquema se ven los vectores campo creado por cada cuerpo y el vector resultante en el punto P.

De esta forma el campo eléctrico resultante en el punto P, tiene un módulo de 4,3x10⁶ N/C, su dirección es horizontal y su sentido es hacia la derecha, tal como muestra la figura de abajo:

Esquema que muestra los cuerpos cargados y el vector campo eléctrico resultante en el punto P que se encuentra en el centro de la línea que une ambos cuerpos. Su dirección es horizontal y su sentido hacia la derecha.

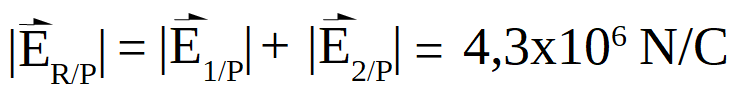
10.2. Caso 2: Campos eléctricos colineales y de sentido opuesto

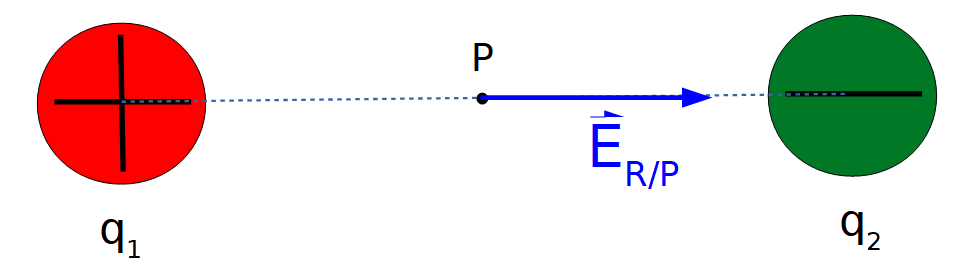
La situación a analizar ahora es:

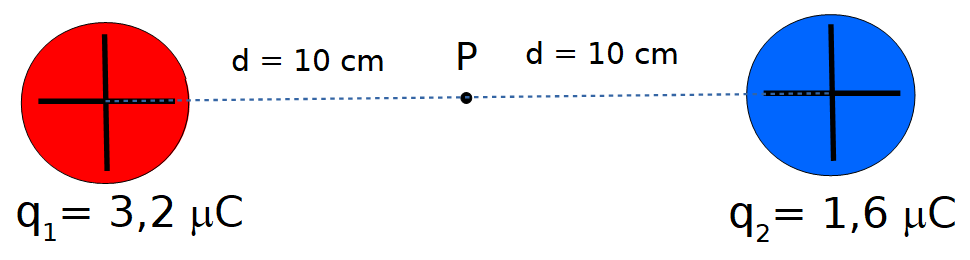
Esquema que muestra dos cargas positivas, q1 de valor 3,2 microCoulomb y q2 de valor 1,6 microCoulomb separadas una distancia de 20 cm. En el punto medio de la recta que une ambas cargas se indica el punto P.

Se desea determinar el Campo eléctrico resultante en el punto P. Para ello se procederá de igual forma que en el caso 1. Se calcula el valor del campo eléctrico que crea cada carga en el punto P. En este caso, los valores son iguales que en el caso 1, por tanto, los módulos de los campos creados por los cuerpos cargados 1 y 2 tendrán el mismo valor que en dicho caso:

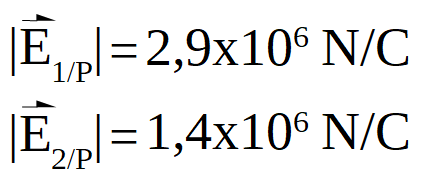
módulo de campo eléctrico creado por la carga 1 en el punto P es igual a 2,9 por diez a la 6 Newton/Coulomb, y el módulo del campo eléctrico creado por la carga 2 en el punto P tiene un valor de 1,4 por diez a la 6 Newton/Coulomb.

Representación del vector campo eléctrico creado por el cuerpo cargado 1 en el punto P:

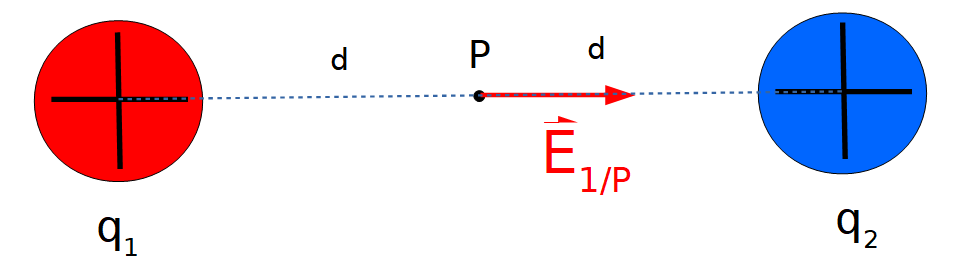
Esquema que muestra dos cuerpos cuyas carga es positiva, q1 y q2, separados una distancia de 20 cm, en el punto medio de la recta que une ambos cuerpos, P, se representó el vector campo eléctrico creado por el cuerpo cargado q1, dicho vector es horizontal hacia la derecha.

Representación del vector campo eléctrico creado por el cuerpo cargado 2 en el punto P:

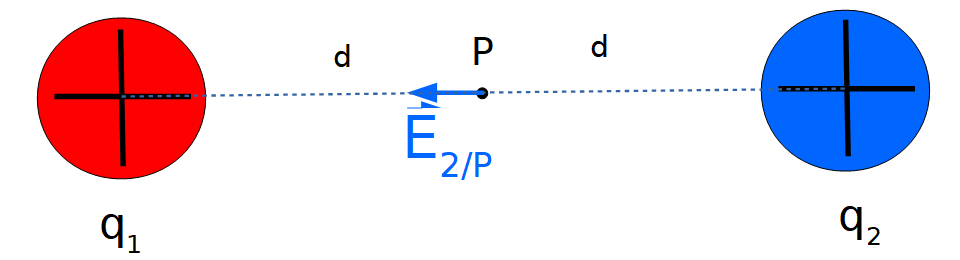
Representación de ambos vectores campo eléctrico en el punto P:

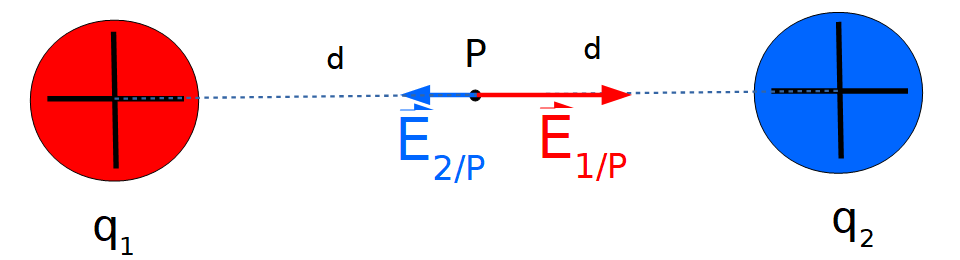
Esquema que muestra dos cuerpos cuyas carga es positiva, q1 y q2, separados una distancia de 20 cm, en el punto medio de la recta que une ambos cuerpos, P, se representaron los vectores campo eléctrico creados por ambos cuerpos cargados, el campo creado por el cuerpo 1 en P es horizontal a la derecha y el creado por el cuerpo 2 es horizontal a la izquierda y su módulo es la mitad del anterior.

Los vectores son colineales y de sentido opuesto por tanto para hallar el resultante la operación es:

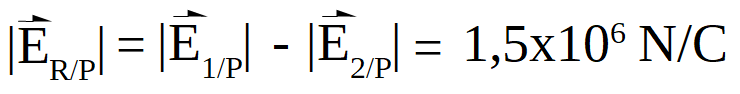
El módulo del campo eléctrico resultante en el punto P es la diferencia de los módulos de los vectores campo creados por cada cuerpo en el punto P, porque los dos vectores tienen igual dirección pero sentido opuesto. Su valor en este caso es 1,5 por diez a la 6 Newton/Coulomb.

A continuación se muestra además el vector resultante en el punto P:

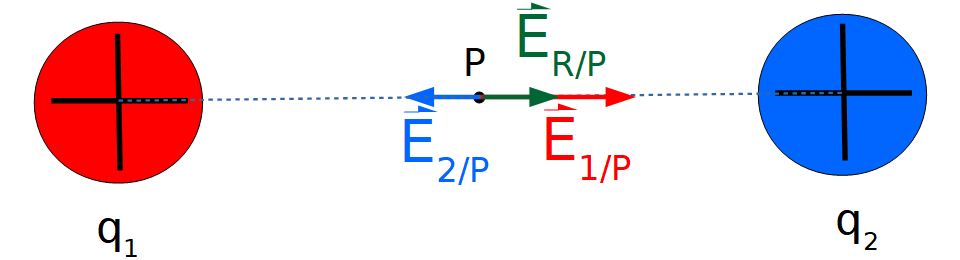
En el mismo esquema que antes se representa además el vector campo eléctrico resultante, su dirección es horizontal, su sentido es hacia la derecha y su valor es la mitad de valor del que es más grande.

Por tanto:

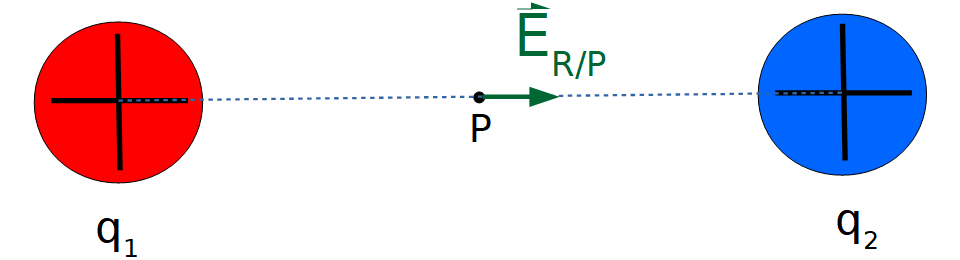
Esquema que muestra el campo eléctrico resultante en el punto medio en la línea que une dos cargas positivas. Su dirección es horizontal y su sentido es hacia la derecha.

10.3. Caso 3: Campos eléctricos no colineales

Se considera ahora la siguiente situación en la que se desea determinar el campo eléctrico resultante en el punto P:

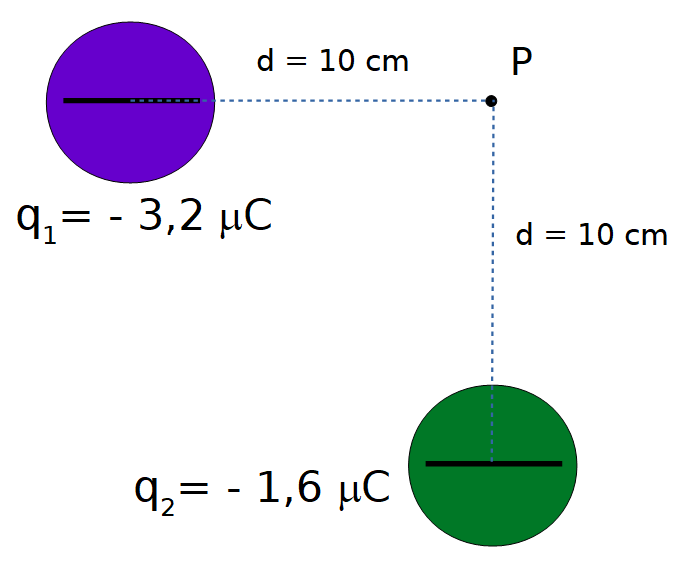
Esquema de dos cuerpos cargados negativamente, cuyos valores de carga son -3,2 y -1,6 microCoulomb. Las cuerpos están ubicados en los vértices opuestos de un cuadrado de lado 10 cm. La q1 se ubica en el vértice superior izquierdo, la q2 en el vértice inferior derecho y el punto P, donde se desea determinar el campo eléctrico resultante, se ubica en el vértice superior derecho del cuadrado.

Los módulos de los campos eléctricos creados por el cuerpo 1 y 2 en el punto P son iguales que en los casos anteriores, pues los valores de las cargas y de las distancias al punto P son iguales.

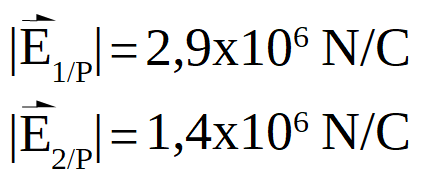
Módulo del campo eléctrico creado por el cuerpo 1 en el punto P es igual a 2,9 por diez a la 6 Newton/Coulomb, y el módulo del campo eléctrico creado por el cuerpo 2 en el punto P es igual a 1,4 por diez a la 6 Newton/Coulomb

Al representar los vectores campo eléctrico creados por cada uno de los cuerpos cargados, se observa que en este caso los vectores son perpendiculares.

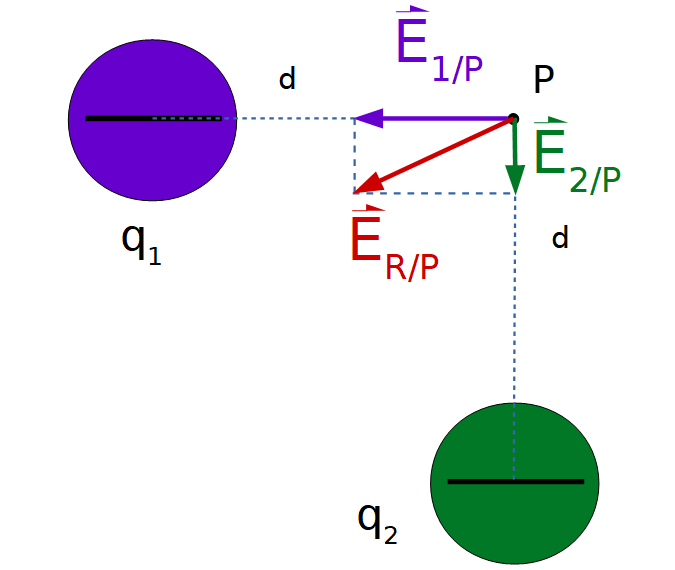
Para poder determinar el vector resultante se puede utilizar el método gráfico o el analítico. Se muestra a continuación el método analítico, que es muy sencillo en este caso si se aplica el Teorema de Pitágoras, para hallar el módulo del vector resultante.

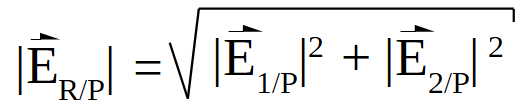
módulo del campo eléctrico resultante en el punto P es igual a la raíz cuadrada de la suma de los cuadrados de los módulos de los campos creados por los cuerpos 1 y 2.

Al sustituir los valores:

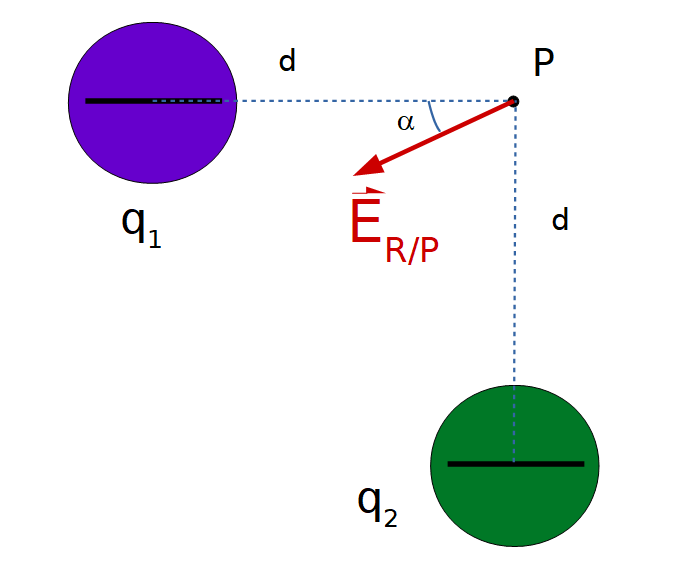
ídem a la imagen anterior, pero sólo se ha representado en el punto P el vector campo eléctrico resultante con el ángulo alfa que forma hacia abajo de la horizontal a la izquierda.

Sólo resta determinar su dirección calculando el ángulo α que forma con la horizontal, utilizando trigonometría, en este caso se usa la función tangente del ángulo:

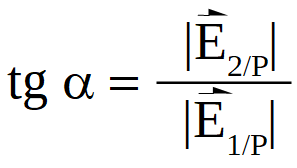
tangente de alfa es igual al módulo del campo creado por el cuerpo 2 dividido entre el módulo del campor creado por el cuerpo 1 en el punto P.

Al sustituir los valores:

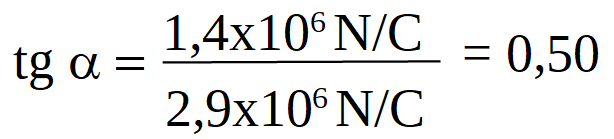
tangente de alfa es igual a 1,4 por diez a la 6 dividido entre 2,9 por diez a la 6, el resultado es 0,50

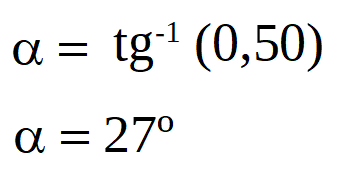
ángulo alfa es igual a tangente a la menos 1 de 0,50, ángulo alfa es igual a 27º.

De esta forma determinamos el vector campo eléctrico resultante en el punto P, su módulo es 3,2x10⁶N/C y su dirección es 27º por debajo de la horizontal hacia la izquierda, o dicho de otra forma su dirección es 27º + 180º = 207º

11. Créditos

Bibliografía

Alvarenga, B. y Máximo, A. (1997). Física general. México: Oxford University.
Egaña, E; Berruti, M. y González, A. (2014). Interacciones 4. Campos y ondas. Uruguay: Contexto.
Hewitt, P. (2007). Física conceptual. México: Pearson-Addison Weasley.

Imágenes, sitios, simuladores y videos

Thales.jpg. Autor: Tomisti. Licencia: Dominio Público.
William Gilbert 45626i.jpg. Autor: Materialscientist. Licencia: Dominio Público.
Charles Francois de Cisternay du Fay.jpg. Autor: Desconocido. Licencia: Dominio Público.
Ben Franklin Duplessis.jpg. Autor: Desconocido. Licencia: Dominio Público.
Electricidad. Wikipedia. Recuperado de: https://es.wikipedia.org/wiki/Electricidad. Licencia: CC BY-SA 3.0.
Charles Augustin de Coulomb. Wikipedia. Licencia: CC BY-SA 3.0.
Balanza de torsión de Coulomb. Autor: Anónimo. Licencia: CC0.
Líneas de campo eléctrico.png. Autor: Chanchocan, Wikimedia. Licencia: CC BY-SA 3.0
Campo de cargas diferentes.png. Autor: Chanchocan, Wikimedia. Licencia: CC BY-SA 3.0.
Líneas de campo.svg. Autor: Jfmelero, Wikimedia. Licencia: CC BY-SA 3.0.
El resto de las imágenes fueron creadas por la autora del recurso, Silvia Pedreira, con licencia CC BY-SA 4.0.
Simulador Globos y electricidad estática. Autor: Podolefsky, N.; Reid, S.; Paul, A. y otros. Universidad de Colorado Boulder. Licencia: CC BY
Correa, I. (2011). Carga eléctrica. Recuperado de: https://www.youtube.com/watch?v=_9uajkA_CYc. Licencia Estándar de YouTube.
Pepenjuto (2007). Campo eléctrico. Recuperado de: https://www.youtube.com/watch?v=6UKxj7cba68. Licencia Estándar de YouTube.
Anteldetodos (2014). Micro Antel Ciencias: Electricidad estática. Recuperado de: https://www.youtube.com/watch?v=M5qUgG0-yQQ. Licencia Estándar de YouTube.
Anteldetodos (2014). Antel Ciencias - Campo eléctrico. Recuperado de: https://www.youtube.com/watch?v=__Hb98dXNIk. Licencia Estándar de YouTube.

Autoría del Módulo: Silvia Pedreira.

spedreira@uruguayeduca.edu.uy

Esta obra está bajo una Licencia Creative Commons Atribución 4.0 Internacional.

Portal Uruguay Educa.

Diciembre de 2019