¿Cómo funciona un calorímetro y una bomba calorimétrica?
| Sitio: | Aulas | Uruguay Educa |
| Curso: | Química - 3º B.D. |
| Libro: | ¿Cómo funciona un calorímetro y una bomba calorimétrica? |
| Imprimido por: | Invitado |
| Día: | jueves, 3 de abril de 2025, 23:50 |
Tabla de contenidos
1. Calorímetro (presión constante)
El calorímetro es un instrumento de laboratorio que permite cuantificar la cantidad de calor liberada o absorbida por un sistema en un determinado proceso.
![]()
Un calorímetro permite determinar el calor a presión constante (QP), midiéndose la variación de temperatura (ΔT).
Se utiliza para estudiar la relación entre el calor suministrado a un sistema y su variación de temperatura, o el calor de un proceso y su variación de temperatura. Se eligen reacciones químicas o cambios físicos de forma en que no haya reactivos ni productos gaseosos.


Imagen del interior y exterior de un calorímetro utilizado en los centros educativos.
![]()

1.1. ¿Cómo está compuesto un calorímetro?
![]()
El calorímetro está formado por:
- Un recipiente con tapa construido de material aislante (a nivel educativo se suele utilizar espuma plast).
- Un termómetro para medir la temperatura del líquido (generalmente agua) o del sistema contenido en el recipiente.
La siguiente figura muestra un corte longitudinal de un calorímetro de uso común en un laboratorio, en ella se muestra sus partes fundamentales:
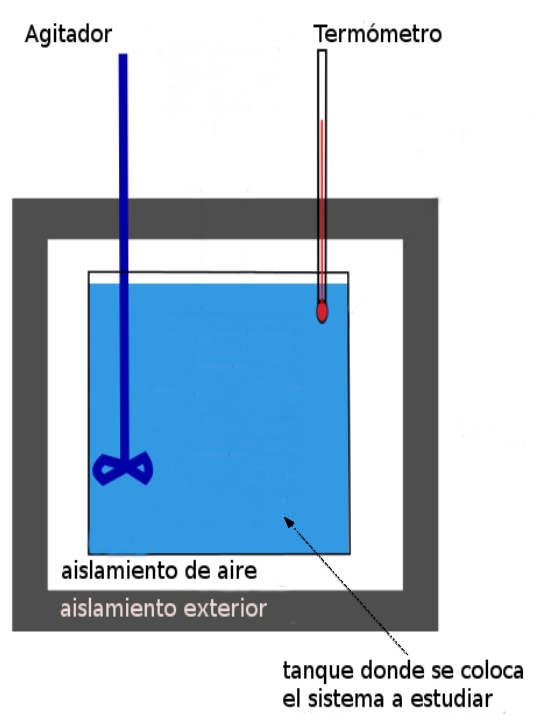
1.2. ¿Cómo se utiliza un calorímetro?
Muchos de los calorímetros usados en los centros educativos de nuestro país no tienen resistencia como se observa en la siguiente imagen.

![]()
![]()
Por ejemplo para conocer el calor absorbido o cedido en un cambio físico a presión constante como la mezcla de dos volúmenes de agua a distinta temperatura:
Se coloca la muestra de agua 1 a temperatura ambiente (se debe conocer con exactitud su masa) dentro del calorímetro y luego de unos minutos se mide la temperatura de la misma utilizando un termómetro.
Luego se coloca la muestra de agua 2 (también se debe conocer su masa con exactitud) que está a mayor temperatura que la 1, por ejemplo, se mezcla con la anterior utilizando el agitador y finalmente se mide la temperatura final del sistema.
Este procedimiento puede servir para determinar la constante térmica de los materiales que forman al calorímetro como se describe en el siguiente capítulo de este material.
![]()
Para poder utilizar un calorímetro las reacciones tienen que ser rápidas, completas y no involucrar reactivos o productos en estado gaseoso. Además el valor de la variación de la entalpía de la reacción debe ser suficiente para que el valor de la variación de la temperatura (ΔT) pueda medirse tomando en cuenta la precisión del termómetro empleado.
Por ejemplo podemos determinar el calor liberado o absorbido a presión constante cuando reaccionan una solución de ácido clorhídrico (HCl) con una solución de hidróxido de sodio (NaOH). La siguiente ecuación química representa el proceso ocurrido (neutralización):
NaOH (ac) + HCl (ac) → NaCl (ac) + H2O (l)
En el recipiente contenedor
se introduce un volumen (V1) de la solución de hidróxido de sodio de concentración conocida y manteniendo la agitación
constante se controla la temperatura del sistema hasta conseguir su estabilización. Con una
pipeta se adicionan un volumen (V2) de solución de ácido clorhídrico de concentración conocida y se
controla el cambio de temperatura que se produce hasta conseguir la nueva temperatura
de estabilización.
Se registran todos los datos obtenidos.
1.3. Constante térmica de los materiales que forman un calorímetro
![]()
La capacidad calorífica de los materiales que forman al calorímetro se denomina a veces constante térmica del calorímetro, y depende de los materiales de los que está hecho el calorímetro y su masa.
La constante térmica (K) está relacionada con el calor (repasa qué es el calor y cómo se calcula en el siguiente enlace) que absorbe o cede el aparato al
realizar determinaciones calorimétricas. Es importante conocer este dato ya que al utilizar un calorímetro parte del calor absorbido o liberado en el cambio que ocurre en su interior (sea físico o químico) va a ser absorbido o cedido por los materiales que forman al calorímetro.
Como la masa (m) y el calor específico del calorímetro son constantes en todas las mediciones que se realicen bajo las mismas condiciones, se define:
K = m . Ce
donde K es la constante térmica de los materiales que forman al calorímetro. El valor de K representa la cantidad de calor necesaria para elevar o disminuir la temperatura del calorímetro en 1 °C.
La constante térmica de los materiales que forman al calorímetro (K) se expresa como J/°C.
Recuerda que para calcular el calor utilizamos la siguiente expresión: Q = m . Ce . ΔT
Por lo que si sustituimos la expresión anterior (K = m . Ce) obtenemos que: Q = K . ΔT
Como sabemos que el proceso ocurre a presión constante podemos decir que: QP K = K . ΔT
Si QP K es el calor absorbido (o cedido) por el calorímetro y ΔT el aumento (o
disminución) de la temperatura experimentada por el calorímetro, la siguiente expresión nos permite calcular la constante térmica de los materiales que forman al calorímetro:
K = QP K / ΔT
2. Bomba calorimétrica (volumen constante)
Para determinar el poder calorífico de una sustancia, como los combustibles o los alimentos, por ejemplo, se utiliza un instrumento llamado bomba calorimétrica. La reacción de combustión se produce en un recipiente metálico cerrado herméticamente donde los gases que intervienen permanecen contenidos en él, es decir que el volumen es constante.
![]()
Una bomba calorimétrica permite determinar el calor a volumen constante (QV).

![]()
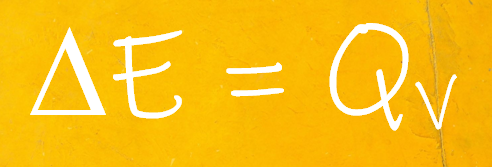
2.1. ¿Cómo está compuesta una bomba calorimétrica?
![]()
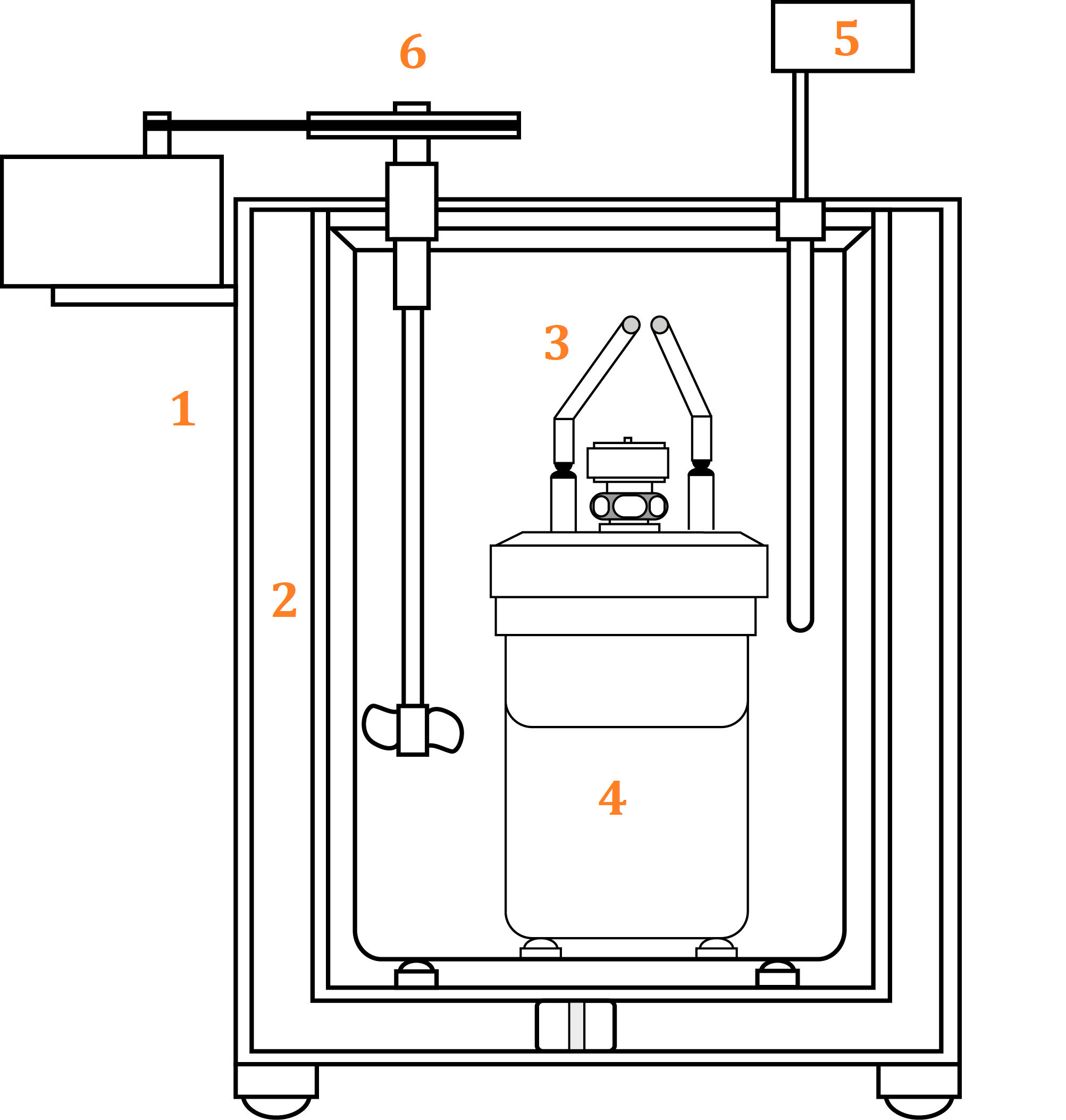
Una bomba calorimétrica está formada por:
- Recipiente externo con aislante.
- Recipiente de acero que contiene el agua que rodea la bomba de acero.
- Cables de encendido.
- Bomba de acero que contiene la cápsula para el combustible.
- Termómetro: para medir la temperatura inicial y final del sistema.
- Agitador para homogeneizar el agua.
2.2. ¿Cómo se utiliza una bomba calorimétrica?
![]()
El combustible o alimento cuyo poder calorífico se desea determinar se coloca en una cápsula para combustible (si el combustible es sólido, deberá colocarse en forma de pastilla) dentro de la bomba calorimétrica. Adicionalmente se agrega el dioxígeno necesario para la combustión. La bomba calorimétrica se rodea de una masa de agua que absorberá el calor liberado por el combustible. Todo esto se realiza dentro de una zona adiabática (zona en la que no hay intercambio de calor con el entorno) para evitar fuga o pérdida de calor que afecte el proceso. Debemos tomar en cuenta que la propia bomba absorbe parte del calor liberado en la combustión debido a que no es un sistema perfectamente adiabático.
Observa el siguiente video breve sobre cómo se utiliza una bomba calorimétrica.
3. ¿Qué es la energía interna?
![]()
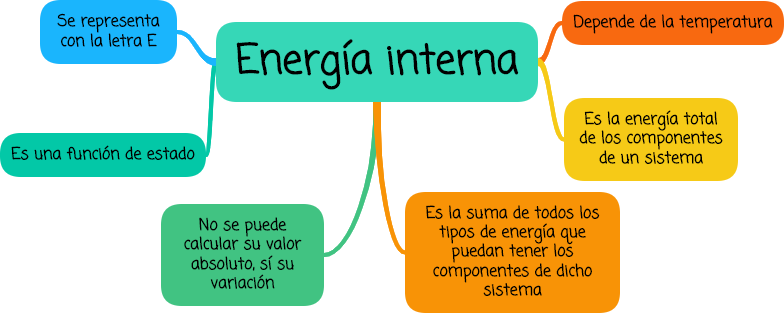
Energía interna es la energía total de los componentes de un sistema y es la suma de todos los tipos de energía que puedan tener los componentes de dicho sistema: energías de los enlaces, de traslación, rotación y vibración de las partículas, etc.
La energía interna es una función de estado que se representa por la letra E (o también con la letra U). Es por definición imposible de calcular el valor absoluto para un sistema en un estado determinado, solo se puede afirmar que depende de la temperatura a la que se encuentra siendo mayor la energía interna del sistema cuanto mayor es la temperatura a la que se encuentra.
Pero sí se puede calcular la variación entre dos estados ΔE = E2 - E1, siendo esta una característica de todas las funciones de estado.
La energía interna es la suma de las energías contenidas en un sistema. En un
sistema químico sería la suma de todas las energías cinéticas y potenciales de las
partículas que lo forman.
4. En resumen
![]()
- Un calorímetro permite determinar QP, la cantidad de calor liberada o absorbida por una reacción o cambio que transcurre a presión constante.
- Se determina la variación de la entalpía (ΔH) de un proceso utilizando un calorímetro.
![]()
- Una bomba calorimétrica permite determinar QV, la cantidad de calor liberada o absorbida por una reacción o cambio que transcurre a volumen constante.
- Se determina la variación de la energía interna (ΔE) de un proceso utilizando una bomba calorimétrica.
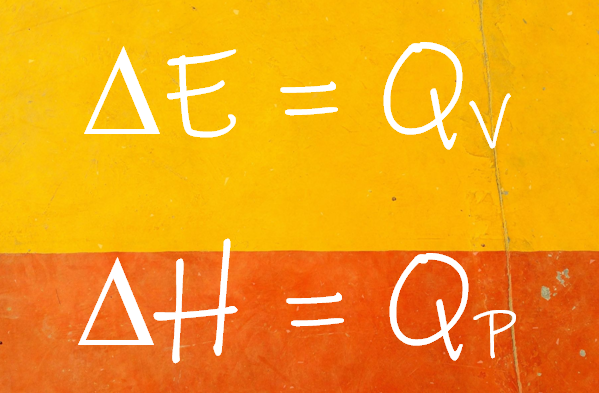
5. Resolución de ejercicios: Ejemplo 1

Una muestra de 50,00 g de agua a 13,50 °C se mezcla con 50,00 g de agua a 70,10 °C, en un calorímetro. Después de transcurrido cierto tiempo el sistema final alcanza el equilibrio térmico. Despreciar la constante térmica de los materiales que forman al calorímetro.
Calcular la temperatura final del sistema.
El calor específico (Ce) del agua líquida es: 4,18 J/g.°C.
- Identificar los datos que da la letra:
Ce agua = 4,18 J/g.°C
Muestra 1:
m1 = 50,00 g
Ti 1 = 13,50 °C
Tf = ?
Muestra 2:
m2 = 50,00 g
Ti 2 = 70,10 °C
Tf = ?
- Planteo:
La conservación de la energía establece que:
- QP 2 = QP 1
El calor liberado a presión constante por la muestra 2 (que se encuentra inicialmente a mayor temperatura que la muestra 1) tiene signo negativo, mientras que el calor absorbido por la muestra 1 (inicialmente a menor temperatura que la muestra 2) tiene signo positivo.
- m2 . Ce agua . ΔT = m1 . Ce agua . ΔT
- m2 . Ce agua . (Tf - Ti1) = m1 . Ce agua . (Tf - Ti2)
Sustituyendo los datos:
- 50,00 g . 4,18 J/g.°C . (Tf - 70,10 °C) = 50,00 g . 4,18 J/g.°C . (Tf - 13,50 °C)
Podemos simplificar la expresión teniendo en cuenta que la masa de agua y el calor específico de ambas muestras es el mismo:
- 50,00 g . 4,18 J/g.°C . (Tf - 70,10 °C) = 50,00 g . 4,18 J/g.°C . (Tf - 13,50 °C)
- (Tf - 70,10 °C) = (Tf - 13,50 °C)
- Tf + 70,10 °C = Tf - 13,50 °C
Reordenando términos:
70,10 °C + 13,50 °C = Tf + Tf
83,60 °C = 2 Tf
83,60 °C / 2 = Tf
41,80 °C = Tf
La temperatura final del sistema es de 41,80 °C.
5.1. Ejemplo 2
![]()
Una muestra de 50,00 mL de una solución 0,400 mol/L de sulfato de cobre (II) a 23,35 °C se mezcla con 50,00 mL de una solución de hidróxido de sodio 0,600 mol/L también a 23,35 °C, en un calorímetro. Después de transcurrida la reacción, la temperatura de la situación final del sistema se mide y es 26,65 °C. La densidad de la solución final es de 1,02 g/mL. El calorímetro tiene una capacidad calorífica (K) de 24,0 J/°C.
La siguiente ecuación química representa lo que ocurre:
CuSO4 (ac) + 2 NaOH (ac) → Cu(OH)2 (s) + Na2SO4 (ac)
Calcular la cantidad de calor liberado en el proceso.
Suponer que el calor específico (Ce) de la mezcla final es el mismo que el del agua líquida: 4,18 J/g.°C.
- Identificar los datos que da la letra:
Ce mezcla = 4,18 J/g.°C
Vmezcla = 50,00 mL + 50,00 mL = 100,00 mL
Ti = 23,35 °C
Tf = 26,65 °C
ΔT= Tf - Ti ΔT= 26,65 - 23,35 = 3,30 °C
K = 24,0 J/°C.
- Planteo:
La cantidad de calor liberado en la reacción se absorbe por la mezcla y el calorímetro (suponiendo despreciable las pérdidas al entorno).
QP reacción = QP situación final del sistema + QP K
Q a presión constante de la situación final del sistema (QP situación final del sistema):
Para hallar el calor se debe conocer la masa de la mezcla final. Para ello se utiliza la expresión matemática de la densidad (d = m/V), despejando la masa.
m = d.V = 1,02 g/mL . 100,00 mL = 102 g
QP situación final del sistema = m . Ce . ΔT
QP situación final del sistema = 102 g . 4,18 J/g.°C . 3,30 °C = 1407 J
Q absorbido por el calorímetro a presión constante (QP K):
QP K = K . ΔT
QP K = 24,0 J/°C . 3,30 °C = 79,2 J
Q reacción a presión constante (QP reacción):
QP reacción = 1407 J + 79,2 J = 1486 J
5.2. Ejemplo 3
![]()
Una fuente térmica transfiere 3,358 kJ a un calorímetro que contiene 50,00 g de agua. La temperatura del agua y del calorímetro, inicialmente a 22,34 °C aumenta hasta 36,74 °C.
El calor específico (Ce) del agua líquida es de 4,18 J/g.°C. La densidad del agua líquida es 1,00 g/mL.
Calcular la capacidad calorífica del calorímetro.
- Identificar los datos que da la letra:
Ce agua = 4,18 J/g.°C
Vagua = 50,00 mL
dagua líquida = 1,00 g/mL
Ti = 22,34 °C
Tf = 36,74 °C
ΔT= Tf - Ti ΔT= 36,74 - 22,34 = 14,40 °C
QP transferido = 3,358 kJ o 3358 J
- Planteo:
QP transferido = QP agua + QP K
Q absorbido por el agua a presión constante (QP agua):
Para hallar el calor se debe conocer la masa del agua. Para ello se utiliza la expresión matemática de la densidad (d = m/V), despejando la masa.
m = d.V = 1,00 g/mL . 50,00 mL = 50,0 g
QP agua = m . Ce . ΔT
QP agua = 50,0 g . 4,18 J/g.°C . 14,40 °C = 3010 J
Q absorbido por el calorímetro a presión constante (QP K):
Despejando de la siguiente ecuación QP transferido = QP agua + QP K sería:QP K = QP transferido - QP agua
QP K = 3358 J - 3010 J = 348 J
Para calcular la capacidad calorífica del calorímetro utilizamos la siguiente expresión: K = QP K / ΔT
K = 348 J / 14,40 °C = 24,2 J/°C
5.3. Ejemplo 4
![]()
¿Cuál es el calor para la combustión completa de una muestra de 1,4350 g de naftaleno (C10H8) en una bomba calorimétrica cuya capacidad calorífica es de 1,80 kJ/ºC, si la temperatura de los 2000 g de agua en su interior aumentó de 20,17 ºC a 25,84 ºC? Recuerda que Ce agua = 4,18 J/g ºC. ¿Y en kJ/mol?
- Identificar los datos que da la letra:
Ce agua = 4,18 J/g.°C
mnaftaleno= 1,4350 g
magua = 2000 g
Ti = 20,17 °C
Tf = 25,84 °C
ΔT= Tf - Ti ΔT= 25,84 - 20,17 = 5,67 °C
K = 1,80 kJ/ºC
- Planteo:
QV combustión = QV agua + QV K
Q absorbido por el agua a volumen constante (QV agua):
QV agua = m . Ce . ΔT
QV agua = 2000 g . 4,18 J/g.°C . 5,67 °C = 47401 J o 47,4 kJ
Q absorbido por la bomba calorimétrica a volumen constante (QV K):
QV K = K . ΔT
QV K = 1,80 kJ/°C . 5,67 °C = 10,2 kJ
Q combustión a volumen constante (QV combustión):
QV combustión = 47,4 kJ + 10,2 kJ = 57,6 kJ
- Al quemarse 1,4350 g de naftaleno se liberaron 57,6 kJ, ¿cuál el calor liberado al quemarse un mol (expresado en kJ/mol)?
Es necesario calcular la masa molar del naftaleno. Repasa cómo hacerlo en el siguiente enlace.
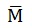 C10H8 = 128 g/mol
C10H8 = 128 g/mol
Con este dato y la masa se puede calcular la cantidad química (n) de naftaleno: n = m / 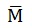
n = 1,4350 g / 128 g/mol = 0,0112 mol
Se liberaron 57,6 kJ en la combustión de 0,0112 mol de naftaleno, por lo que 1 mol de naftaleno: QV combustión por mol = QV combustión / n
QV combustión por mol = 57,6 kJ / 0,0112 mol = 5143 kJ/mol
6. Relación entre la variación de entalpía y la variación de la energía interna
Se pueden relacionar el calor a presión constante (QP) con el calor a volumen constante (QV) como se muestra en la siguiente expresión:
ΔH = ΔE + P.ΔV
O reordenando los términos;
ΔH - ΔE = P.ΔV
Tomando en cuenta que QP = ΔH y que QV = ΔE, entonces podemos llegar a la siguiente expresión:
QP - QV = P.ΔV
![]()
Cuando la reacción química tiene lugar entre productos y reactivos en fase líquida o sólida podemos admitir que QP = QV puesto que en estos casos no hay cambio apreciable de volumen ΔV ≈ 0.
![]()
Cuando en la reacción existen reactivos en estado gaseoso tomando en cuenta la relación ΔH = ΔE + P.ΔV
Si hacemos la aproximación de suponer a estos gases como ideales (que siguen la ley general de los gases, se puede utilizar la expresión P.V = n.R.T):
QP = QV + Δn.R.T
y en este caso si no hay variación en la cantidad química se cumple la igualdad QP = QV
________________________________
Recuerda que:
- P: presión
- V: volumen
- n: cantidad química
- T: temperatura
- R: constante universal de los gases.
7. Créditos
Autoría de los materiales utilizados: Profesora Anarella Gatto.
Esta obra está bajo una Licencia Creative Commons Atribución 4.0 Internacional.
Bibliografía consultada:
- Alegría, M., Bosack, A., Deprati, A., Dal Fávero, M., Franco, R., Jaul, M. y Morales, E. (1999). Química II Dinámica de las transformaciones. Introducción a la Química biológica, ambiental e industrial. Argentina: Santillana.
- Atkins. P. y Jones, L. (2005). Principios de Química. (3era edición). Editorial Panamericana.
- Calorimetría. Recuperado de: http://campus.usal.es/~quimfis/apoyo/Cachaza/Personal/practicas/CALORIMETRIA
- Castellan, G. (1998). Físicoquímica. (2da edición). México: Pearson.
- Chang, R. (2007). Química. (9na edición). Mc Graw Hill.
- I.E.S. Manuel Reina (s.f.). TEMA 3º: TERMOQUÍMICA. Departamento de Física y Química. Recuperado de: http://www.juntadeandalucia.es/averroes/centros-tic/14006217/helvia/aula/archivos/repositorio/0/34/html/quimica2temas/TEMA%203Termoquimica.pdf
- Masterton, W. y Hurley, C. (2004). Principios y reacciones. (4ta edición). Madrid, España: Thomson.
- Saravia, G., Segurola, B., Franco, M. y Nassi, M. (2012). Todo se transforma. Química- 4º Año (1º BD). Montevideo, Uruguay: Contexto.
- Whitten, K., Davis, R. y Peck, M. (1998). Química General. (Quinta edición). Madrid, España: Mc Graw Hill.
Vídeos, páginas y/o simuladores utilizados:
David Read . (2008, septiembre 16). Bomb calorimetry [Archivo de Video]. Youtube. https://youtu.be/ohyA9amFfscmarieanton13 . (2015, septiembre 23). BOMBA CALORIMETRICA UNSa [Archivo de Video]. Youtube. https://youtu.be/Vu4W7DVOZQY
Las imágenes utilizadas fueron tomadas de:
- Calorímetro. Autor: Lanzi. Licencia: Dominio Público CC0, vía Wikimedia Commons.
- Calorímetro de laboratorio. Autor: Anarella Gatto. Licencia: CC BY-SA 4.0.
- Bomb calorimeter scheme. Autor: Ichwarsnur. Licencia: CC BY-SA 4.0.
- Bombenkalorimeter_mit_bombe. Autor: Harbor1. Licencia: CC BY 3.0.