Ley de Hess y sus aplicaciones
| Sitio: | Aulas | Uruguay Educa |
| Curso: | Química - 3º B.D. |
| Libro: | Ley de Hess y sus aplicaciones |
| Imprimido por: | Invitado |
| Día: | jueves, 3 de abril de 2025, 20:41 |
1. Introducción
![]()
Como has repasado en el módulo anterior (entalpía estándar de formación y de combustión) se puede determinar la entalpía de reacción estándar a partir del valor obtenido en tablas de las entalpías de formación estándar. Podemos decir que este es el método directo.
![]()
En este módulo se analizará un método indirecto. Muchos compuestos no se pueden sintetizar directamente a partir de sus sustancias simples. En algunos casos, la reacción se lleva a cabo con demasiada lentitud o suceden reacciones secundarias que producen otras sustancias además del compuesto de interés. En estos casos los valores de ΔH°f se determinan por un procedimiento indirecto, que se basa en la Ley propuesta por Hess.
Germain Henri Hess (8 de agosto de 1802 - 30 de noviembre de 1850).
Para saber más sobre Hess consultar el siguiente enlace.
2. Ley de Hess
![]()
Si ciertos reactivos se convierten en determinados productos (en las mismas condiciones), la variación de la entalpía tiene el mismo valor independientemente que el proceso se realice en uno o en varios pasos.
En otras palabras, es posible separar la reacción de interés en una serie de reacciones para las cuales se pueda medir el valor de ΔH°r y, de esta manera, calcular el ΔH°r para la reacción total (de interés).
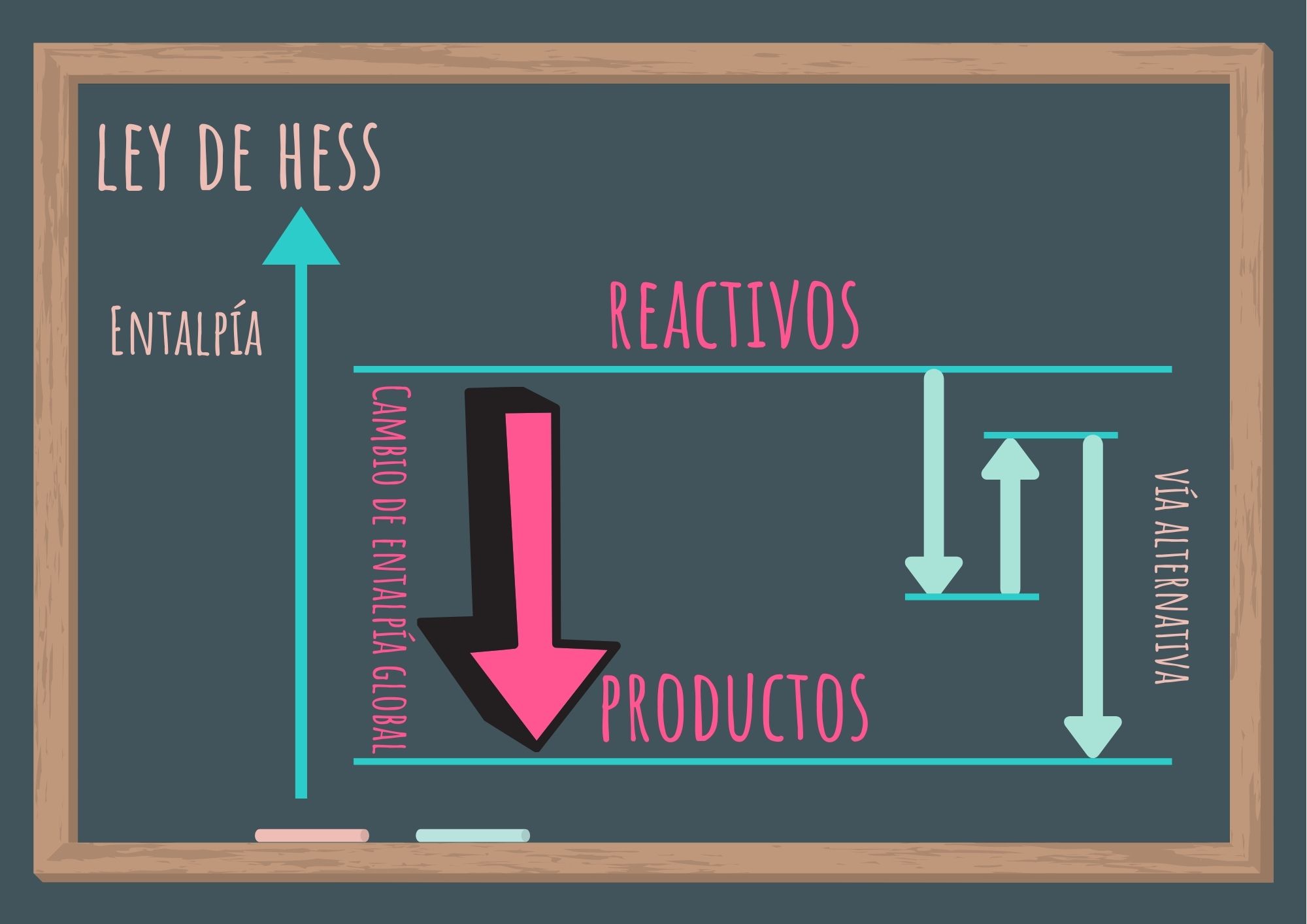
La ley de Hess no es otra cosa que la consecuencia de que la entalpía es una función de estado.
2.1. Ejemplo 1
![]()
La variación de entalpía del proceso de obtención de dióxido de carbono a partir de carbono grafito y dioxígeno gaseoso tiene el mismo valor ya sea que la transformación tenga lugar en una etapa o en dos etapas.
Proceso en una etapa:
C (graf) + O2 (g) → CO2 (g) ΔH1 = - 393 kJ
Proceso en dos etapas:
C (graf) + ½ O2 (g) → CO (g) ΔH2 = - 111 kJ
CO (g) + ½ O2 (g) → CO2 (g) ΔH3 = - 282 kJ
ΔH1 = ΔH2 + ΔH3
- 393 kJ = - 111 kJ + (- 282 kJ)
- 393 kJ = - 393 kJ
Si se parte de carbono grafito y dioxígeno gaseoso y se obtiene dióxido de carbono (CO2) gaseoso, el calor liberado es siempre 393 kJ/mol. No importa si se forma directamente dióxido de carbono o si en una primera etapa se obtiene monóxido de carbono (CO) y este luego reacciona con más dioxígeno produciéndose CO2, gaseoso.
2.2. Ejemplo 2
![]()
Se puede sintetizar cloruro de sodio sólido a partir de sodio metálico y dicloro gaseoso mediante dos métodos diferentes.
- Método 1:
Na (s) + H2O (l) → NaOH (s) + ½ H2 (g) ΔH°r = - 139,78 kJ
½ H2 (g) + ½ Cl2 (g) → HCl (g) ΔH°r = - 92,31 kJ
HCl (g) + NaOH (s) → NaCl (s) + H2O (l) ΔH°r = - 179,06 kJ
____________________________________________________________
Reacción global: Na (s) + ½ Cl2 (g) → NaCl (s) ΔH°reacción global= - 411,15 kJ
- Método 2:
½ H2 (g) + ½ Cl2 (g) → HCl (g) ΔH°r = - 92,31 kJ
Na (s) + HCl (g) → NaCl (s) + ½ H2 (g) ΔH°r = - 318,84 kJ
____________________________________________________________
Reacción global: Na (s) + ½ Cl2 (g) → NaCl (s) ΔH°reacción global= - 411,15 kJ
La reacción global se obtiene sumando todas las reacciones de la secuencia. La variación neta de la entalpía se obtiene sumando todas las variaciones de entalpía de la secuencia. Como puedes observar sin importar el número de pasos o etapas en las que se lleve a cabo el proceso, la variación de la entalpía de la reacción global es la misma.
![]()
En el siguiente video puedes observar la reacción global entre el gas dicloro y el sodio metálico para formar cloruro de sodio. Como puedes ver al agregar una gota de agua sobre el sodio metálico comienza la reacción, y luego de la explosión se observa un polvo de color blanco (cloruro de sodio sólido).
3. ¿Cómo usar la ley de Hess?
![]()
La regla general para aplicar la ley de Hess es que se debe acomodar una serie de reacciones químicas (correspondientes a la serie de etapas) de tal manera que, cuando se sumen, se cancelen todas las especies excepto los reactivos y productos que aparecen en la reacción global.
Si la reacción global es una reacción de formación de un compuesto, esto significa que deben quedar las sustancias simples del lado de los reactivos (izquierda de la flecha) y el compuesto de interés del lado de los productos (derecha de la flecha).
Para lograr esto, con frecuencia se tiene que multiplicar alguna o todas las ecuaciones que representan las etapas individuales, por los coeficientes apropiados.
![]()
Para utilizar la ley de Hess, se debe buscar una secuencia de reacciones que al sumarse se obtenga la reacción de interés.
- Paso 1: Seleccionar uno de los reactivos en la reacción global y escribir una ecuación química en la que este también aparezca como un reactivo.
- Paso 2: Seleccionar uno de los productos en la reacción global y escribir una ecuación química en la que este también aparezca como un producto. Agregar esta ecuación a la ecuación escrita en el paso 1.
- Paso 3: Suprimir las especies no deseadas en la suma obtenida en el paso 2 mediante el agregado de una ecuación que tenga la misma sustancia o sustancias en el lado opuesto (si es un reactivo, que en la nueva ecuación aparezca como un producto, y si es un producto, que en la nueva ecuación aparezca como un reactivo).
- Paso 4: Una vez completada la secuencia, combinar las entalpías de reacción estándar.

![]()
Importante: recuerda las dos propiedades ya analizadas de la entalpía en módulos anteriores (propiedad extensiva y transformaciones reversibles). En cada paso puede ser necesario invertir la ecuación o multiplicar por un factor. Si se quiere invertir una ecuación química hay que cambiar el signo del valor de la entalpía de reacción. Si se multiplican los coeficientes estequiométricos por un factor, se debe multiplicar la entalpía de reacción por el mismo factor.
3.1. Resolución de ejercicios: Ejemplo 1
![]()
Se desea conocer la entalpía estándar de formación del metano. A continuación se representa dicho proceso de formación:
C (graf) + 2 H2 (g) → CH4 (g) (reacción global)
Esta reacción no se puede llevar a cabo así como se representa, así que es imposible medir el cambio de entalpía en forma directa. Se debe emplear un método indirecto, utilizando la ley de Hess. Para empezar se han estudiado las siguientes reacciones y se conoce sus valores de ΔH°r.
a. C (graf) + O2 (g) → CO2 (g) ΔH°r= - 393,5 kJ
b. H2 (g) + ½ O2 (g) → H2O (l) ΔH°r= - 285,8 kJ
c. CH4 (g) + 2 O2 (g) → 2 H2O (l) + CO2 (g) ΔH°r= - 890,2 kJ
Procedimiento:
- Siguiendo el paso 1 seleccionamos la ecuación a. en la que el carbono grafito ya se encuentra como reactivo y con el mismo coeficiente estequiométrico que tiene en la reacción global.
1. C (graf) + O2 (g) → CO2 (g) ΔH°r= - 393,5 kJ
Luego seleccionamos la ecuación b. en la que el dihidrógeno gaseoso ya se encuentra también como reactivo, pero no tiene el mismo coeficiente estequiométrico que en la reacción global, por lo que multiplicamos toda la ecuación por el factor 2.
(H2 (g) + ½ O2 (g) → H2O (l) ΔH°r= - 285,8 kJ) x 2
2. 2 H2 (g) + O2 (g) → 2 H2O (l) ΔH°r= - 285,8 kJ x 2 = - 571,6 kJ
- Para el paso 2 seleccionamos la ecuación c. en la que el metano está como reactivo y debe aparecer como producto en la reacción global por lo que debemos invertir esta ecuación colocando como reactivos los productos originales de la ecuación c. y como productos los reactivos originales (recordando que se invierte el signo de la entalpía de la reacción, es negativo y queda positivo).
3. 2 H2O (l) + CO2 (g) → CH4 (g) + 2 O2 (g) ΔH°r= + 890,2 kJ
Obtenemos entonces:
1. C (graf) + O2 (g) → CO2 (g) ΔH°r= - 393,5 kJ
2. 2 H2 (g) + O2 (g) → 2 H2O (l) ΔH°r= - 571,6 kJ
3. 2 H2O (l) + CO2 (g) → CH4 (g) + 2 O2 (g) ΔH°r= + 890,2 kJ
- En el paso 3 suprimimos aquellas sustancias que aparezcan en las mismas cantidades como reactivos en una ecuación y como productos en otra.
1. C (graf) + O2 (g) → CO2 (g) ΔH°r= - 393,5 kJ
2. 2 H2 (g) + O2 (g) → 2 H2O (l) ΔH°r= - 571,6 kJ
3. 2 H2O (l) + CO2 (g) → CH4 (g) + 2 O2 (g) ΔH°r= + 890,2 kJ
En la ecuación 2. aparecen dos moles de agua como producto y en la ecuación 3. la misma cantidad de agua como reactivo.
En las ecuaciones 1. y 2. aparecen un mol de dioxígeno gaseoso (sumando dos moles) como reactivo en cada caso, y en la ecuación 3. hay dos moles de dioxígeno gaseoso como producto.
- Para finalizar (paso 4) sumamos las entalpías de las 3 reacciones para obtener así la entalpía de la reacción global:
1. C (graf) + O2 (g) → CO2 (g) ΔH°r= - 393,5 kJ
2. 2 H2 (g) + O2 (g) → 2 H2O (l) ΔH°r= - 571,6 kJ
3. 2 H2O (l) + CO2 (g) → CH4 (g) + 2 O2 (g) ΔH°r= + 802,5 kJ
______________________________________________________________
C (graf) + 2 H2 (g) → CH4 (g) ΔH°reacción global= - 393,5 kJ + (- 571,6 kJ) + 890,2 kJ
![]()
C (graf) + 2 H2 (g) → CH4 (g) ΔH°reacción global = - 74,9 kJ
3.2. Ejemplo 2
![]()
Estudiando la síntesis del propano (C3H8) un gas utilizado como combustible en los campamentos:
3 C (graf) + 4 H2 (g) → C3H8 (g) (reacción global)
Es difícil medir el cambio de entalpía de esta reacción. Sin embargo, las entalpías estándar de combustión son fáciles de medir. Se dispone de los siguientes datos experimentales, calcula el ΔH°reacción global de la reacción de formación.
a. C3H8 (g) + 5 O2 (g) → 3 CO2 (g) + 4 H2O (l) ΔH°r = - 2220,0 kJ
b. C (graf) + O2 (g) → CO2 (g) ΔH°r = - 393,5 kJ
c. H2 (g) + ½ O2 (g) → H2O (l) ΔH°r = - 285,8 kJ
Procedimiento:
- Siguiendo el paso 1 seleccionamos la ecuación b. en la que el carbono grafito ya se encuentra como reactivo, pero con diferente coeficiente estequiométrico con respecto a la reacción global, por lo que multiplicamos toda la ecuación por el factor 3.
(C (graf) + O2 (g) → CO2 (g) ΔH°r = - 393,5 kJ) x 3
1. 3 C (graf) + 3 O2 (g) → 3 CO2 (g) ΔH°r= - 393,5 kJ x 3 = - 1180,5 kJ
Luego seleccionamos la ecuación c. en la que el dihidrógeno gaseoso ya se encuentra también como reactivo, pero no tiene el mismo coeficiente estequiométrico que en la reacción global, por lo que multiplicamos toda la ecuación por el factor 4.
(H2 (g) + ½ O2 (g) → H2O (l) ΔH°r= - 285,8 kJ) x 4
2. 4 H2 (g) + 2 O2 (g) → 4 H2O (l) ΔH°r= - 285,8 kJ x 4 = - 1143,2 kJ
- Para el paso 2 seleccionamos la ecuación a. en la que el propano está como reactivo y debe aparecer como producto en la reacción global por lo que debemos invertir esta ecuación colocando como reactivos los productos originales de la ecuación a. y como productos los reactivos originales (recordando que se invierte el signo de la entalpía de la reacción, es negativo y queda positivo).
3. 4 H2O (l) + 3 CO2 (g) → C3H8 (g) + 5 O2 (g) ΔH°r= + 2220 kJ
Obtenemos entonces:
1. 3 C (graf) + 3 O2 (g) → 3 CO2 (g) ΔH°r= - 1180,5 kJ
2. 4 H2 (g) + 2 O2 (g) → 4 H2O (l) ΔH°r= - 1143,2 kJ
3. 4 H2O (l) + 3 CO2 (g) → C3H8 (g) + 5 O2 (g) ΔH°r= + 2220 kJ
- En el paso 3 suprimimos aquellas sustancias que aparezcan en las mismas cantidades como reactivos en una ecuación y como productos en otra.
1. 3 C (graf) + 3 O2 (g) → 3 CO2 (g) ΔH°r= - 1180,5 kJ
2. 4 H2 (g) + 2 O2 (g) → 4 H2O (l) ΔH°r= - 1143,2 kJ
3. 4 H2O (l) + 3 CO2 (g) → C3H8 (g) + 5 O2 (g) ΔH°r= + 2220 kJ
En la ecuación 2. aparecen cuatro moles de agua como producto y en la ecuación 3. la misma cantidad de agua como reactivo.
En las ecuaciones 1. y 2. aparecen tres moles de dioxígeno gaseoso y dos moles (sumando cinco moles) como reactivo en cada caso, y en la ecuación 3. hay cinco moles de dioxígeno gaseoso como producto.
- Para finalizar (paso 4) sumamos las entalpías de las 3 reacciones para obtener así la entalpía de la reacción global:
1. 3 C (graf) + 3 O2 (g) → 3 CO2 (g) ΔH°r= - 1180,5 kJ
2. 4 H2 (g) + 2 O2 (g) → 4 H2O (l) ΔH°r= - 1143,2 kJ
3. 4 H2O (l) + 3 CO2 (g) → C3H8 (g) + 5 O2 (g) ΔH°r= + 2220 kJ
______________________________________________________________
3 C (graf) + 4 H2 (g) → C3H8 (g) ΔH°reacción global= - 1180,5 kJ + (- 1143,2 kJ) + 2220 kJ

3 C (graf) + 4 H2 (g) → C3H8 (g) ΔH°reacción global = - 103,7 kJ
3.3. Ejemplo 3
![]()
Se desea conocer la entalpía estándar de la siguiente reacción:
Mg (s) + ½ O2 (g) → MgO (s) (reacción global)
Conociendo la entalpía estándar de formación del agua, y determinando experimentalmente las entalpías estándares de reacción del magnesio metálico (Mg) y del óxido de magnesio (MgO) con una solución de ácido clorhídrico (HCl), es posible obtener la entalpía de la combustión del magnesio.
Determina dicho valor a partir de las siguientes ecuaciones:
a. H2 (g) + ½ O2 (g) → H2O (l) ΔH°r= - 285,8 kJ
b. Mg (s) + 2 HCl (ac) → MgCl2 (ac) + H2 (g) ΔH°r= - 307,4 kJ
c. MgO (s) + 2 HCl (ac) → MgCl2 (ac) + H2O (l) ΔH°r= + 8,4 kJ
Procedimiento:
- Siguiendo el paso 1 seleccionamos la ecuación b. en la que el magnesio sólido ya se encuentra como reactivo y con el mismo coeficiente estequiométrico que tiene en la reacción global.
1. Mg (s) + 2 HCl (ac) → MgCl2 (ac) + H2 (g) ΔH°r= - 307,4 kJ
Luego seleccionamos la ecuación a. en la que el dioxígeno gaseoso ya se encuentra también como reactivo y con el mismo coeficiente estequiométrico que tiene en la reacción global.
2. H2 (g) + ½ O2 (g) → H2O (l) ΔH°r= - 285,8 kJ
- Para el paso 2 seleccionamos la ecuación c. en la que el óxido de magnesio está como reactivo y debe aparecer como producto en la reacción global por lo que debemos invertir esta ecuación colocando como reactivos los productos originales de la ecuación c. y como productos los reactivos originales (recordando que se invierte el signo de la entalpía de la reacción, es positivo y queda negativo).
3. MgCl2 (ac) + H2O (l) → MgO (s) + 2 HCl (ac) ΔH°r= - 8,4 kJ
Obtenemos entonces:
1. Mg (s) + 2 HCl (ac) → MgCl2 (ac) + H2 (g) ΔH°r= - 307,4 kJ
2. H2 (g) + ½ O2 (g) → H2O (l) ΔH°r= - 285,8 kJ
3. MgCl2 (ac) + H2O (l) → MgO (s) + 2 HCl (ac) ΔH°r= - 8,4 kJ
- En el paso 3 suprimimos aquellas sustancias que aparezcan en las mismas cantidades como reactivos en una ecuación y como productos en otra.
1. Mg (s) + 2 HCl (ac) → MgCl2 (ac) + H2 (g) ΔH°r= - 307,4 kJ
2. H2 (g) + ½ O2 (g) → H2O (l) ΔH°r= - 285,8 kJ
3. MgCl2 (ac) + H2O (l) → MgO (s) + 2 HCl (ac) ΔH°r= - 8,4 kJ
En la ecuación 2. aparece un mol de agua como producto y en la ecuación 3. la misma cantidad de agua como reactivo.
- Para finalizar (paso 4) sumamos las entalpías de las 3 reacciones para obtener así la entalpía de la reacción global:
1. Mg (s) + 2 HCl (ac) → MgCl2 (ac) + H2 (g) ΔH°r= - 307,4 kJ
2. H2 (g) + ½ O2 (g) → H2O (l) ΔH°r= - 285,8 kJ
3. MgCl2 (ac) + H2O (l) → MgO (s) + 2 HCl (ac) ΔH°r= - 8,4 kJ
______________________________________________________________
Mg (s) + ½ O2 (g) → MgO (s) ΔH°reacción global= - 307,4 kJ + (- 285,8 kJ) + (- 8,4 kJ)

Mg (s) + ½ O2 (g) → MgO (s) ΔH°reacción global = - 601,6 kJ
![]()
4. Créditos
Autoría de los materiales utilizados: Profesora Anarella Gatto.
Esta obra está bajo una Licencia Creative Commons Atribución 4.0 Internacional.
Bibliografía consultada:
- Atkins. P. y Jones, L. (2005). Principios de Química. (3era edición). Editorial Panamericana.
- Castellan, G. (1998). Físicoquímica. (2da edición). México: Pearson.
- Chang, R. (2007). Química. (9na edición). Mc Graw Hill.
- Masterton, W. y Hurley, C. (2004). Principios y reacciones. (4ta edición). Madrid, España: Thomson.
- Saravia, G., Segurola, B., Franco, M. y Nassi, M. (2012). Todo se transforma. Química- 4º Año (1º BD). Montevideo, Uruguay: Contexto.
- Whitten, K., Davis, R. y Peck, M. (1998). Química General. (Quinta edición). Madrid, España: Mc Graw Hill.
Vídeos, páginas y/o simuladores utilizados:
luis alberto Molina. (2012, 16 de octubre). SODIO Y AGUA EN CLORO. [Archivo de video]. Recuperado de: https://www.youtube.com/watch?v=mBpFDL_sjIg&feature=youtu.be - Profesor Rodrigo Araya. (2014, 14 de diciembre). Combustion de una cinta de magnesio. [Archivo de video]. Recuperado de: https://www.youtube.com/watch?v=XyrOvg3pS88&feature=youtu.be
- Germain Henri Hess. (s.f.). En Wikipedia. Recuperado el 16 de diciembre de 2020 de https://es.wikipedia.org/wiki/Germain_Henri_Hess
Las imágenes utilizadas fueron tomadas de:
- Hess_Germain_Henri. Autor: Литография П. А. Смирнова Licencia: Dominio Público.