¿Qué relación hay entre la concentración de los reactivos y la rapidez de una reacción?
| Sitio: | Aulas | Uruguay Educa |
| Curso: | Química - 3º B.D. |
| Libro: | ¿Qué relación hay entre la concentración de los reactivos y la rapidez de una reacción? |
| Imprimido por: | Invitado |
| Día: | sábado, 5 de abril de 2025, 00:10 |
Tabla de contenidos
1. Introducción
¿Qué relación hay entre la concentración de los reactivos y la rapidez de una reacción? A medida que las concentraciones de los reactivos cambian a temperatura constante, la rapidez de reacción cambia.
![]()
Se puede escribir la expresión de la ley de rapidez (o también denominada ley de velocidad) para una reacción con el objetivo de describir de qué manera su rapidez depende de las concentraciones.
La ley de rapidez se deduce experimentalmente para cada reacción a partir de un estudio de cómo varía la rapidez con la concentración.
La expresión de la ley de rapidez en la que A y B son reactivos (A + B → P) tiene la forma general:
r = k. [A]x . [B]y
Siendo:
- r: rapidez.
- k: constante específica de rapidez.
- [A]: concentración del reactivo A.
- x: orden parcial del reactivo A.
- [B]: concentración del reactivo B.
- y: orden parcial del reactivo B.
Los valores de los exponentes x e y, y de la constante k, no necesariamente guardan relación con los coeficientes estequiométricos de la ecuación química ajustada para la reacción global y se deben determinar experimentalmente.
Las potencias a las que se elevan las concentraciones, x e y, son normalmente números enteros o cero, pero en ocasiones son fraccionarios o aún negativos.
Una potencia de 1 significa que la rapidez es directamente proporcional a la concentración de ese reactivo.
Una potencia de 2 significa que la rapidez es directamente proporcional al cuadrado de esa concentración.
Una potencia de 0 significa que la rapidez no depende de la concentración de ese reactivo, siempre que haya algo de reactivo presente.
El valor x se dice que es el orden parcial u orden de la reacción con respecto a A, e y es el orden parcial u orden de la reacción con respecto a B.
![]()
El orden global de la reacción es la suma algebraica de los exponentes, por ejemplo x e y.
Orden global = x + y + ...


1.1. Ejemplos de orden parcial y global
Analicemos los siguientes ejemplos:
![]()
3 NO (g) → N2O (g) + NO2 (g)
La ley de rapidez para esta reacción es la siguiente: r = k . [NO]2- x = 2
- y = 0 ya que no hay otro reactivo.
- orden global = x + y = 2 + 0 = 2
Es de segundo orden parcial respecto a NO (monóxido de nitrógeno) y de segundo orden global.
![]()
2 NO2 (g) + F2 (g) → 2 NO2F (g)
La ley de rapidez para esta reacción es la siguiente: r = k . [NO2] . [F2]- x = 1
- y = 1
- orden global = x + y = 1 + 1 = 2
Es de primer orden parcial respecto a NO2 (dióxido de nitrógeno), de primer orden parcial respecto a F2 (diflúor) y de segundo orden global.
![]()
H2O2 (ac) + 3 I- (ac) + 2 H+ (ac) → 2 H2O (l) + I3- (ac)
La ley de rapidez para esta reacción es la siguiente: r = k . [H2O2] . [I-]- x = 1
- y = 1
- z = 0
- orden global = x + y + z = 1 + 1 + 0 = 2
Es de primer orden parcial respecto a H2O2 (peróxido de hidrógeno), de primer orden parcial respecto a I- (anión ioduro o yoduro), de orden cero respecto a H+ (catión hidrógeno) y de segundo orden global.
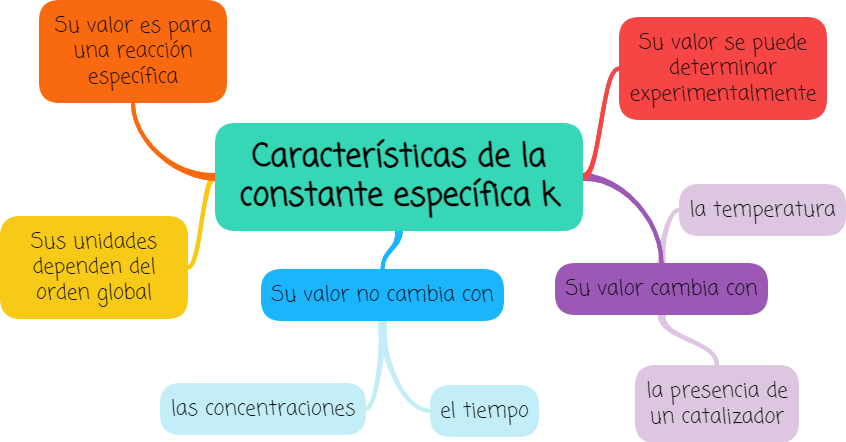
1.2. Constante específica k
![]()
Su valor es para una reacción específica, representada por una ecuación ajustada.
Sus unidades dependen del orden global de la reacción.
Su valor no cambia con las concentraciones tanto de reactivos como de productos.
Su valor no cambia con el tiempo.
Se valor refiere a la reacción a una temperatura determinada y cambia si cambiamos la temperatura.
Su valor depende de si está presente o no un catalizador.
Su valor se puede determinar experimentalmente para la reacción en condiciones adecuadas.
2. ¿Cómo se puede determinar experimentalmente la ley de rapidez?
Si se realizan pares de experimentos, a la misma
temperatura, en los que cada uno solamente difiera del otro en la
concentración de un reactivo, se pueden determinar la ley de rapidez.
![]()
El siguiente procedimiento es útil para determinar la ley de rapidez a través del método de las concentraciones iniciales.
- Paso 1: Escribe la ley de rapidez general.
- Paso 2: Selecciona dos experimentos en los que el reactivo A se mantenga con la misma concentración.
- Paso 3: Escribe la ley de rapidez para cada uno de los dos experimentos sustituyendo el valor de r (rapidez) por el dato experimental en cada caso.
- Paso 4: Divide ambas expresiones.
- Paso 5: Simplifica los términos iguales.
- Paso 6: Despeja el valor del orden parcial del reactivo B.
- Paso 7: Selecciona dos experimentos en los que el reactivo B se mantenga con la misma concentración.
- Paso 8: Repite los pasos anteriores hasta obtener el orden parcial del reactivo A.
- Paso 9: Selecciona uno de los experimentos y sustituye los órdenes que has hallado para calcular el valor de la constante k.
- Paso 10: Escribe la ley de rapidez indicando el valor de k, los órdenes parciales y el orden global.

2.1. Resolución de ejercicios: Ejemplo 1
![]()
Se obtuvieron los siguientes datos en el laboratorio para la reacción entre el diflúor gaseoso y el dióxido de cloro gaseoso:
F2 (g) + 2 ClO2 (g) → 2 FClO2 (g)
Experimento | [F2] (mol/L) | [ClO2] (mol/L) | rinicial (mol/L.s) |
1 | 0,10 | 0,010 | 1,2.10-3 |
2 | 0,10 | 0,040 | 4,8.10-3 |
3 | 0,20 | 0,010 | 2,4.10-3 |
![]()
1. Comenzamos escribiendo la ley de la rapidez de forma general: r = k [F2]x. [ClO2]y
![]()
2. Selecciono los dos experimentos en donde la concentración del reactivo A, en ese caso el diflúor no cambia, en este caso el experimento 1 y el 2.
![]()
3. Sustituyo los valores para cada caso:
- r1 = k [0,10 mol/L]x. [0,010 mol/L]y = 1,2 . 10-3 mol/L.s
- r2 = k [0,10 mol/L]x. [0,040 mol/L]y = 4,8 . 10-3 mol/L.s
![]()
4. Divido ambas expresiones, colocando como numerador la expresión en la que el reactivo B, en este caso el dióxido de cloro, tiene una mayor concentración.
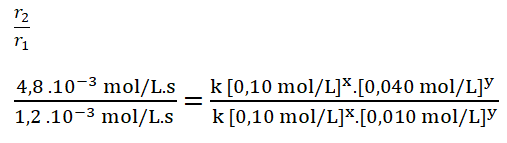
![]()
5. Simplifico aquellos términos iguales aplicando una cancelación:
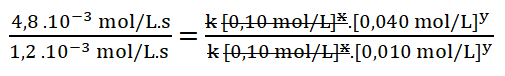
Divido los valores numéricos de la rapidez 2 sobre la 1.
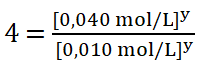
Divido entre sí los valores de la concentración del reactivo B aplicando la división de dos potencias de igual exponente: 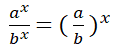
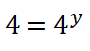
Como tengo dos potencias iguales de igual base (4), sus exponentes deben ser iguales: ![]()
![]()
6. Despejo el valor del orden parcial o potencia y, obtengo que: ![]()
![]()
7. Repito los pasos anteriores seleccionando un experimento en donde la concentración del reactivo B se mantenga constante.
Selecciono los experimentos 1 y 3 en donde la concentración del reactivo B no cambia, en este caso el dióxido de cloro.
Sustituyo lo valores para cada experimento:
- r1 = k [0,10 mol/L]x. [0,010 mol/L]y = 1,2 . 10-3 mol/L.s
- r3 = k [0,20 mol/L]x. [0,010 mol/L]y = 2,4 . 10-3 mol/L.s
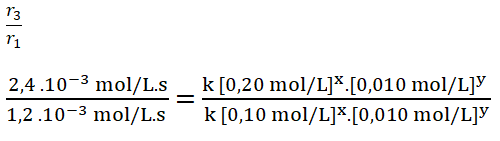
Simplifico los términos iguales.
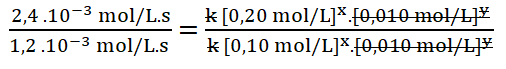
Divido los valores numéricos de la rapidez 3 sobre la 1.
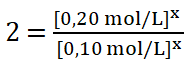
Divido entre sí los valores de la concentración del reactivo A.
![]()
![]()
8. Despejo el valor del orden parcial o potencia x, obtengo que: ![]()
![]()
9. Selecciono uno de los experimentos, sustituyo los datos y despejo k (constante específica).
1,2 .10-3 mol/L.s = k. 0,10 mol/L. 0,010 mol/L
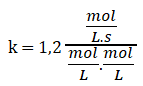
Simplificando las unidades:
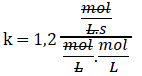
Finalmente:
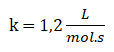
![]()
10. Escribo la ley de rapidez: r = 1,2 L/mol.s [F2]1. [ClO2]1 o r = 1,2 L/mol.s [F2]. [ClO2]
Orden global = 1+1 = 2
2.2. Ejemplo 2
![]()
Determina con los siguientes datos:
a) la ley de rapidez incluyendo el orden global.
b) el valor de k.
c) la rapidez cuando [NO] = 12,0.10-3 mol/L y [H2] = 6,06.10-3 mol/L.
|
2 H2 (g) + 2 NO (g) → N2 (g) + 2 H2O (g) |
|||
|
Experimento |
[H2] (mol/L) |
[NO] (mol/L) |
rinicial (mol/L.s) |
|
1 |
2,0.10-3 |
5,0.10-3 |
1,3.10-5 |
|
2 |
2,0.10-3 |
10,0.10-3 |
5,0.10-5 |
|
3 |
4,0.10-3 |
10,0.10-3 |
10,0.10-5 |

1. Comenzamos escribiendo la ley de la rapidez de forma general: r = k [H2]x. [NO]y

2. Selecciono los dos experimentos en donde la concentración del reactivo A, en ese caso el dihidrógeno no cambia, en este caso el experimento 1 y el 2.

3. Sustituyo los valores para cada caso:
- r1 = k [2,0.10-3 mol/L]x. [5,0.10-3mol/L]y = 1,3.10-5 mol/L.s
- r2 = k [2,0.10-3 mol/L]x. [10,0.10-3 mol/L]y = 5,0.10-5 mol/L.s

4. Divido ambas expresiones, colocando como numerador la expresión en la que el reactivo B, en este caso el monóxido de nitrógeno, tiene una mayor concentración.
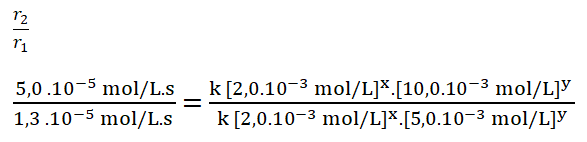

5. Simplifico aquellos términos iguales aplicando una cancelación:
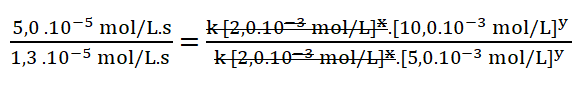
Divido los valores numéricos de la rapidez 2 sobre la 1. Redondeo el resultado a un número entero (4) ya que el resultado es un número decimal (3,8).
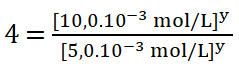
Divido entre sí los valores de la concentración del reactivo B aplicando la división de dos potencias de igual exponente.
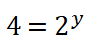

6. Dos al cuadrado es igual a 4 por lo que despejo el valor del orden parcial o potencia y, obtengo que: 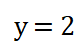

7. Repito los pasos anteriores seleccionando un experimento en donde la concentración del reactivo B se mantenga constante.
Selecciono los experimentos 2 y 3 en donde la concentración del reactivo B no cambia, en este caso el monóxido de nitrógeno.
Sustituyo lo valores para cada experimento:
- r2 = k [2,0.10-3 mol/L]x. [10,0.10-3 mol/L]y = 5,0.10-5 mol/L.s
- r3 = k [4,0.10-3 mol/L]x. [10,0.10-3 mol/L]y = 10,0.10-5 mol/L.s
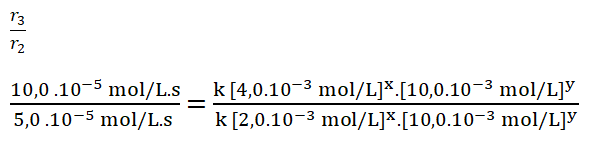
Simplifico los términos iguales.
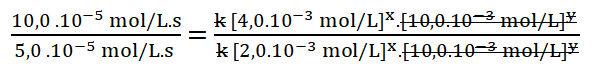
Divido los valores numéricos de la rapidez 3 sobre la 2.
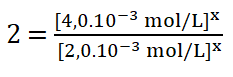
Divido entre sí los valores de la concentración del reactivo A.
![]()

8. Despejo el valor del orden parcial o potencia x, obtengo que: ![]()

9. Selecciono uno de los experimentos, sustituyo los datos y despejo k (constante específica).
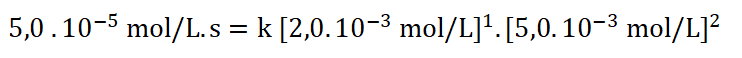
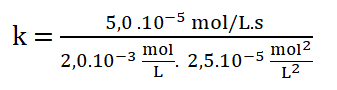
Simplificando las unidades:
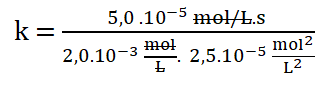
Finalmente:
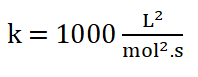

10. Escribo la ley de rapidez: r = 1000 L2/mol2.s [H2]1. [NO]2 o r = 1000 L2/mol2.s [H2]. [NO]2
Orden global = 1+2 = 3
____________________________
Para resolver la parte C debo sustituir los datos brindados en la expresión de la ley de rapidez determinada:
r = 1000 L2/mol2.s [6,06.10-3 mol/L]. [12,0.10-3 mol/L]2
r = 8,73 .10-4 mol/L.s
2.3. Ejemplo 3
![]()
Determina la ley de rapidez y el valor de k con los siguientes datos:
A + 2 B → AB2 | |||
Experimento | [A] (mol/L) | [B] (mol/L) | rinicial (mol/L.s) |
1 | 0,010 | 0,010 | 1,5.10-4 |
2 | 0,010 | 0,020 | 1,5.10-4 |
3 | 0,020 | 0,030 | 6,0.10-4 |

1. Comenzamos escribiendo la ley de la rapidez de forma general: r = k [A]x. [B]y

2. Selecciono los dos experimentos en donde la concentración del reactivo A no cambia, en este caso el experimento 1 y el 2.

3. Sustituyo los valores para cada caso:
- r1 = k [0,010 mol/L]x. [0,010 mol/L]y = 1,5.10-4 mol/L.s
- r2 = k [0,010 mol/L]x. [0,020 mol/L]y = 1,5.10-4 mol/L.s

4. Divido ambas expresiones, colocando como numerador la expresión en la que el reactivo B, en este caso el monóxido de nitrógeno, tiene una mayor concentración.
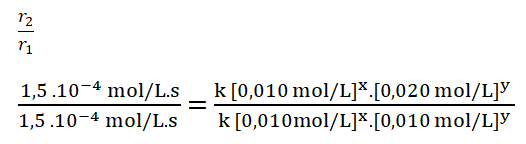

5. Simplifico aquellos términos iguales aplicando una cancelación:
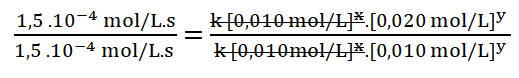
Divido los valores numéricos de la rapidez 2 sobre la 1.
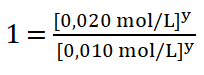
Divido entre sí los valores de la concentración del reactivo B aplicando la división de dos potencias de igual exponente.
![]()

6. Despejo el valor del orden parcial o potencia y aplicando la propiedad de las potencias (cualquier número distinto de cero elevado a la cero da uno) y obtengo que: ![]()

7. Repito los pasos anteriores seleccionando un experimento en donde la concentración del reactivo B se mantenga constante.
Selecciono los experimentos 2 y 3 en donde la concentración del reactivo B no cambia.
Sustituyo lo valores para cada experimento:
- r2 = k [0,010 mol/L]x. [0,020 mol/L]y = 1,5.10-4 mol/L.s
- r3 = k [0,020 mol/L]x. [0,030 mol/L]y = 6,0.10-4 mol/L.s
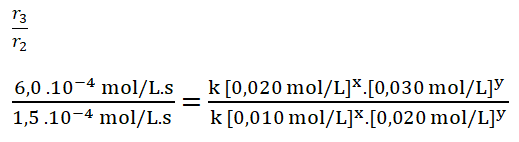
Simplifico los términos iguales tomando en cuenta también que el valor de y es cero, por lo que las concentraciones de B elevadas al exponente cero dan como resultado uno (a0 = 1, siendo a distinto de cero).
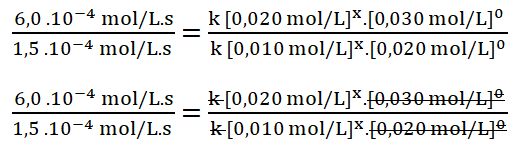
Divido los valores numéricos de la rapidez 3 sobre la 2.
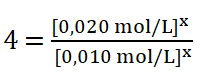
Divido entre sí los valores de la concentración del reactivo A.
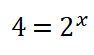

8. Despejo el valor del orden parcial o potencia x, obtengo que: 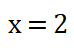

9. Selecciono uno de los experimentos, sustituyo los datos y despejo la k (constante específica).
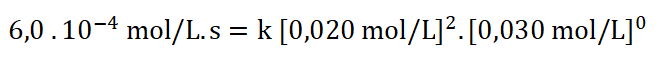
Despejo k:
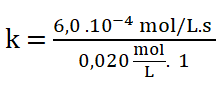
Simplificando las unidades:
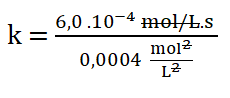
Finalmente:
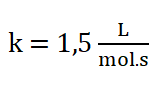

10. Escribo la ley de rapidez: r = 1,5 L/mol.s [A]2. [B]0 o r = 1,5 L/mol.s [A]2
Orden global = 2+0 = 2
2.4. En resumen: ley de rapidez
![]()
 |
Las leyes de rapidez siempre se determinan en forma experimental. A partir de la concentración de los reactivos y de la rapidez inicial es posible determinar el orden de una reacción, y entonces, la constante de rapidez de reacción. |
|---|---|
 |
El orden de una reacción siempre se define en términos de las concentraciones de los reactivos (no de los productos). |
 |
El orden parcial de un reactivo no se relaciona con el coeficiente estequiométrico del reactivo en la reacción global balanceada. |
Observa el siguiente video:
3. Tipos de reacciones según el orden
![]()
Las reacciones químicas pueden clasificarse según el orden global de reacción.
Tenemos de este modo, reacciones de orden global cero, de primer orden, de segundo orden, de tercer orden, según como resulte influida la rapidez de reacción por la concentración de los reactivos bajo un conjunto de condiciones determinada.
La siguiente tabla resume información al respecto de cada orden global:
Orden global de reacción | Descripción | Ejemplo | Ecuación | Unidad de k |
| La rapidez no depende de la concentración del reactivo. | A → P | r = k | mol/L.s |
| La rapidez es directamente proporcional a la concentración de uno de los reactivos. | A → P | r = k . [A] | 1/s o s-1 |
| La rapidez es proporcional al producto de la concentración de dos reactivos o a la segunda potencia de uno de los reactivos. | A + B → P o A → P | r = k . [A] . [B] r = k . [A]2 | L/mol.s |
| La rapidez es proporcional al producto de la concentración de tres términos de concentración. | A + B + C → P | r = k . [A] . [B] . [C] | L2/mol2.s |
4. Comparación gráfica de reacciones de distinto orden
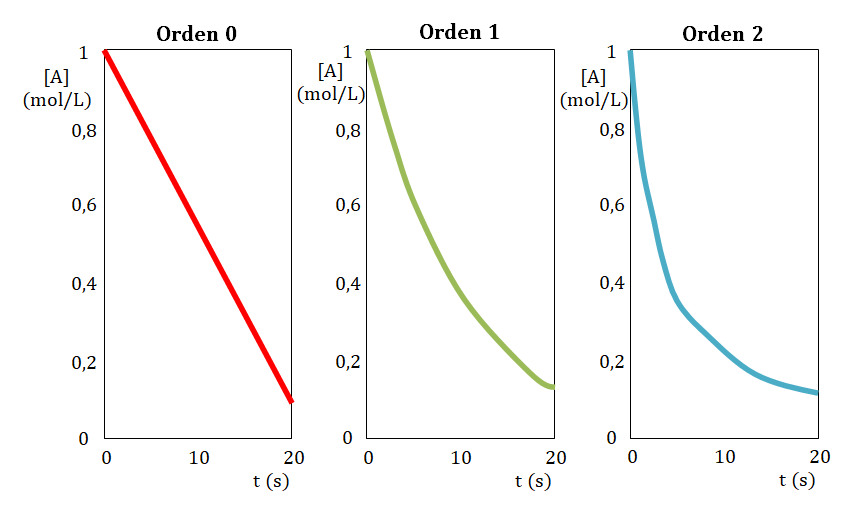
Al construir gráficas de concentración frente al tiempo se obtienen diferentes resultados según el orden global de la reacción.
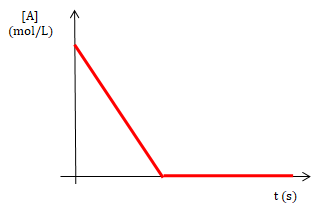
Para una reacción de orden global 0, una gráfica de [A] y tiempo da una línea
recta cuya pendiente es un valor constante (k) y el valor de la
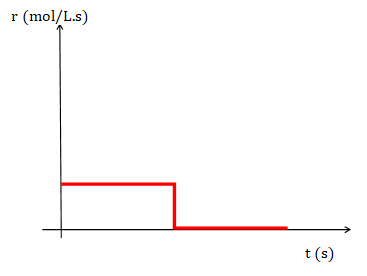
ordenada al origen es [A]0 o concentración inicial del reactivo A. Si se representa la rapidez y el tiempo se obtiene la siguiente gráfica en la que se puede observar que la rapidez es constante y luego pasa a ser 0 cuando todo el reactivo A se ha transformado en producto.
![]()
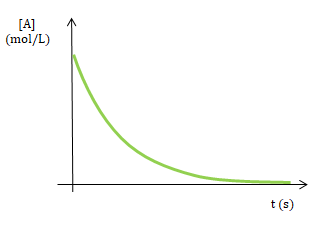
Para una reacción de orden global 1 la rapidez es proporcional a la concentración del reactivo. Como se puede observar al transcurrir el tiempo la concentración del reactivo disminuye.
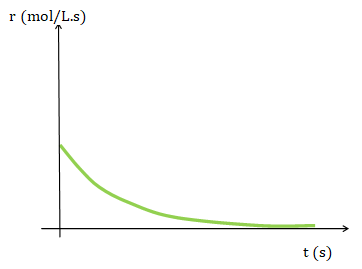
![]()
Para una reacción de orden global 2 la rapidez es proporcional al cuadrado de la concentración y la disminución en la rapidez al avanzar la reacción es mayor que en el caso de una reacción de orden global 1.
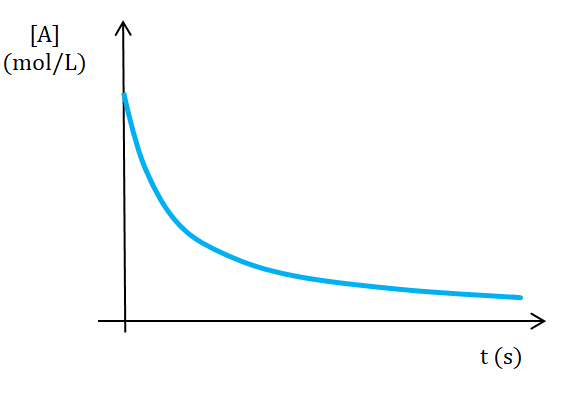
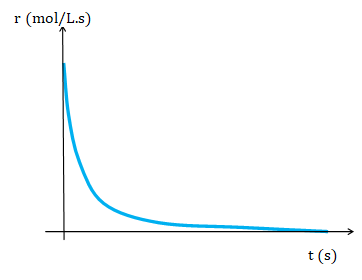
![]()
Al realizar una actividad experimental se suelen obtener datos de concentración al variar el tiempo. ¿Cómo se puede determinar el orden a partir de esos datos?
Primeramente construye la gráfica de tiempo en función de la concentración, si la resultante de la misma es una línea recta el orden con respecto al reactivo estudiado es cero.
En caso de no obtener una línea recta, construye la gráfica tiempo en función de logaritmo de la concentración, si la resultante de la misma es una línea recta el orden con respecto al reactivo estudiado es uno.
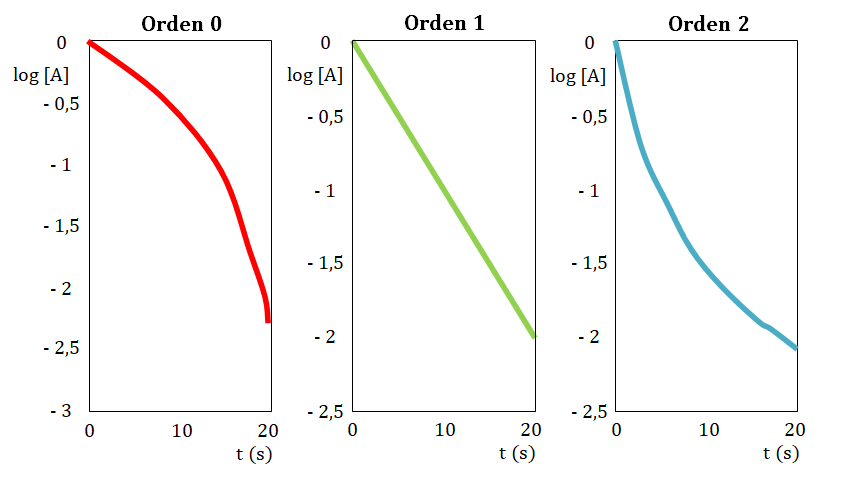
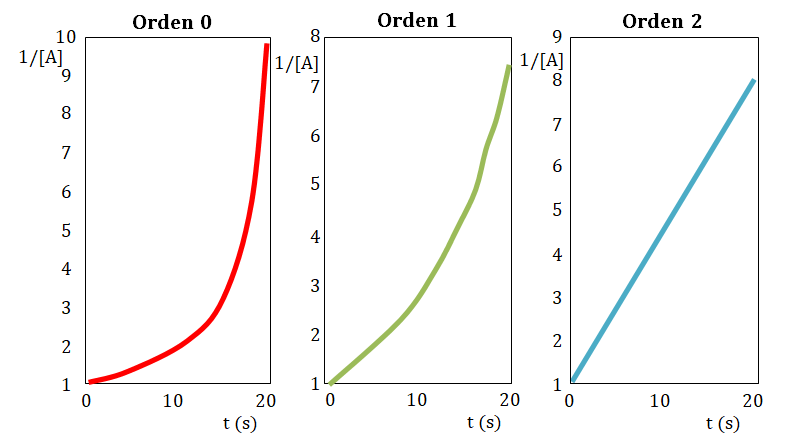
En caso de nuevamente no obtener una línea recta, construye la gráfica tiempo en función del inverso de la concentración, si la resultante de la misma es una línea recta el orden con respecto al reactivo estudiado es dos.
5. Créditos
Autoría de los materiales utilizados: Profesora Anarella Gatto.
Portal Uruguay Educa - Mayo 2021.
Esta obra está bajo una Licencia Creative Commons Atribución 4.0 Internacional.
Bibliografía consultada:
- Atkins. P. y Jones, L. (2005). Principios de Química. (3era edición). Editorial Panamericana.
- Castellan, G. (1998). Físicoquímica. (2da edición). México: Pearson.
- Chang, R. (2007). Química. (9na edición). Mc Graw Hill
- Macías, N. (s.f.). Cinética Química 1603. http://depa.fquim.unam.mx/amyd/archivero/apuntesparte1_10172.pdf
- Masterton, W. y Hurley, C. (2004). Principios y reacciones. (4ta edición). Madrid, España: Thomson.
- Soto, S., Jiménez, D. y Ramírez, I. (2016). Cinética. Vicerrectoría de Docencia CEDA - TEC Digital. https://repositoriotec.tec.ac.cr/bitstream/handle/2238/10111/Cin%C3%A9tica.pdf?sequence=1&isAllowed=y
- UAM (2011). Cinética. Fundamentos de Química. Grado en Física. http://www.qfa.uam.es/labqui/presentaciones/Tema4.pdf
- Whitten, K., Davis, R. y Peck, M. (1998). Química General. (Quinta edición). Madrid, España: Mc Graw Hill.
Vídeos, páginas y/o simuladores utilizados:
Quimiayudas . (2019, 6 de julio). Ley de velocidad: Orden de reacción y Constante de velocidad [Archivo de video]. Youtube. https://youtu.be/_cd9Q3xUFWU- The ChemCollective. (2016). Kinetics Studies of the Bleaching of Food Dyes. http://chemcollective.org/chem/kinetics/index.php
- Número 1. Autor: Freepik. Licencia: Gratis para uso personal o comercial con atribución.
- Número 2. Autor: Freepik. Licencia: Gratis para uso personal o comercial con atribución.
- Número 3. Autor: Freepik. Licencia: Gratis para uso personal o comercial con atribución.
- Número 0. Autor: Freepik. Licencia: Gratis para uso personal o comercial con atribución.
- Número 1. Autor: Freepik. Licencia: Gratis para uso personal o comercial con atribución.
- Número 2. Autor: Freepik. Licencia: Gratis para uso personal o comercial con atribución.
- Número 3. Autor: Freepik. Licencia: Gratis para uso personal o comercial con atribución.



