Astronomía - 1º B.D.
Simulando la experiencia de Eratóstenes
Los antiguos griegos sabían que la Tierra era redonda. La primera persona en calcular la circunferencia de la Tierra fue Eratóstenes de Cirene, que vivió entre del 276 aC al 195 aC.
Eratóstenes sabía que en el solsticio de verano al mediodía local, el Sol se hallaba directamente por encima de la ciudad de Siena (en el cenit). Esto se debe a que Siena se encuentra en el trópico de Cáncer. Observa en la imagen la localidad de Siena.
También sabía que al mediodía local en Alejandría, en la misma fecha, el sol se hallaba desplazado 7 grados respecto del cenit (el punto más alto en el cielo). Mueve con el puntero del ratón el punto D hasta que el ángulo solar valga 7 grados aproximadamente. La distancia entre Siena y la locación D en este caso es de aproximadamente 800 kilómetros.
Es así que Eratóstenes utiliza esta información (el ángulo solar y la distancia entre las dos ciudades para calcular la circunferencia de la Tierra.
Puedes manipular un experimento similar por ti mismo. Mueve el punto D alrededor del círculo. Los rayos del Sol son líneas casi paralelas, pues el astro rey está muy lejos en relación al tamaño de la Tierra.
El punto A es el centro de la Tierra.
La línea de puntos AD es oblicua a estas líneas paralelas de luz solar. De ello se deduce que el ángulo del Sol en D es igual al ángulo central en A. (Las distancias se muestran en kilómetros.) La circunferencia de la Tierra se calcula mediante la resolución de la proporción (distancia entre ciudades) / (perímetro) = (ángulo central) / (360 °).
Un ejemplo, considerando que a un ángulo de 7 grados le corresponde una separación entre ciudades de 800 kilómetros.
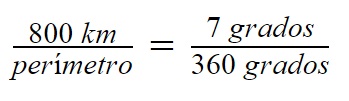
Desafío I. Halla el valor del perímetro de la Tierra para este caso. Resuelve en tu cuaderno de notas.
Desafío II. Podemos asegurar que el perímetro de la Tierra es igual a 3,14 veces el diámetro terrestre. Conociendo el perímetro, ¿puedes averiguar el valor del diámetro terrestre? Resuelve en tu cuaderno de notas e intercambia ideas con compañeros/as de clase.
Esquema manipulable en Geogebra de usuario astronomía_uy (Daniel Gastelú) a partir de proyecto de David Radcliffe.
