Física - 1º B.D.
Fuerza magnética
3. Fuerza magnética sobre un conductor recto por el que circula corriente y que se encuentra en una región en la que existe un campo magnético
3.4. Módulo de la fuerza magnética sobre un conductor recto por el que circula corriente
Si retomamos la Ley de Lorentz:
![]()
Considerando que las cargas se mueven con velocidad constante y se desplazan una longitud L en un intervalo de tiempo, podemos escribir la velocidad como:
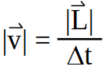
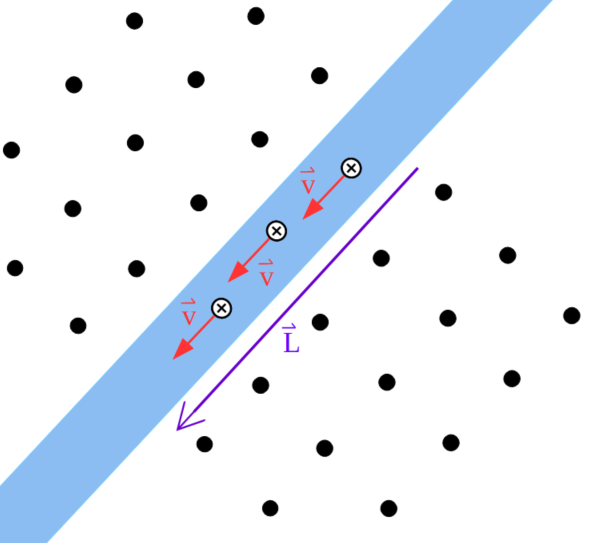
siendo ![]() , el módulo del desplazamiento de las cargas en el conductor inmerso dentro del campo magnético y Δt el intervalo de tiempo que tarda en hacerlo.
, el módulo del desplazamiento de las cargas en el conductor inmerso dentro del campo magnético y Δt el intervalo de tiempo que tarda en hacerlo.
Sustituyendo obtenemos:
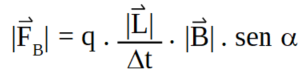
Reordenamos la ecuación:
![]()
Recordando que la intensidad de corriente es:
![]()
Sustituimos:
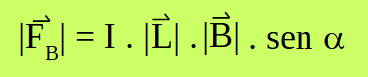
Ley de Laplace
