Física - 3º C.B.

Al analizar la velocidad en el movimiento anterior:

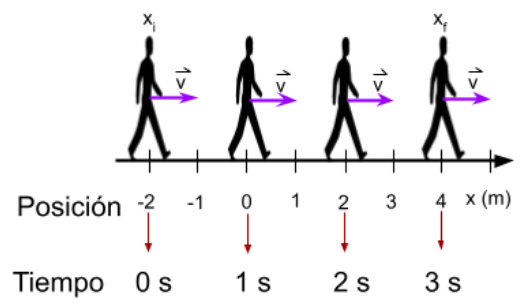
La gráfica del módulo de la velocidad en función del tiempo para este movimiento es una recta paralela al eje del tiempo porque la velocidad permanece constante en los 3 segundos considerados.

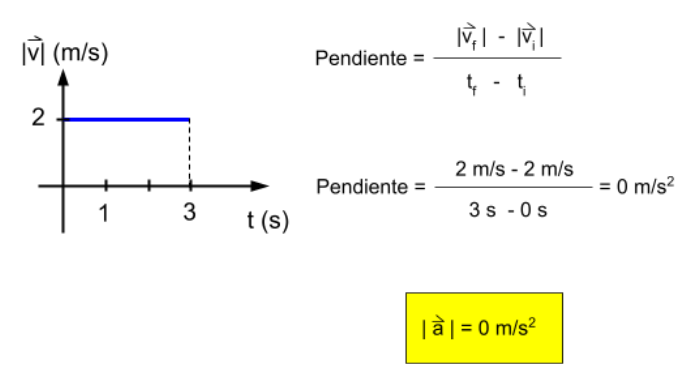
También se puede calcular el área bajo esta gráfica.

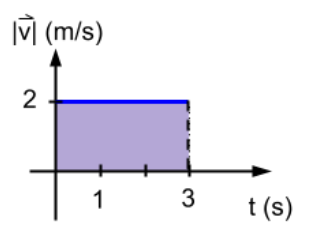
El área bajo la curva corresponde al área de un rectángulo que se determina base por altura. La base es el tiempo, en este caso 3 segundos y la altura es el valor de la velocidad 2 m/s. Al analizar las unidades se observa que queda en metros (m). El significado físico de este cálculo es el módulo del desplazamiento de la persona. El desplazamiento es una magnitud vectorial, se determina como el vector posición final menos el vector posición inicial. A continuación se muestran los vectores posición inicial y final, y se determina el desplazamiento con todas sus características.

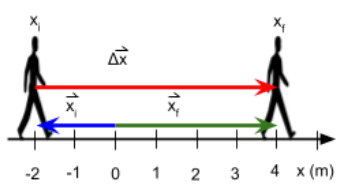
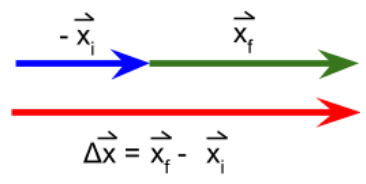
Observa que el módulo del vector desplazamiento es 6 m, esto coincide con el valor determinado con el área bajo la gráfica.

De esta forma el vector desplazamiento es 6 m, 0º o 6 m horizontal a la derecha.

Recuerda que 0º indica que el vector forma 0º con respecto al eje x.