Física - 1º B.D.

Si consideramos el siguiente circuito:

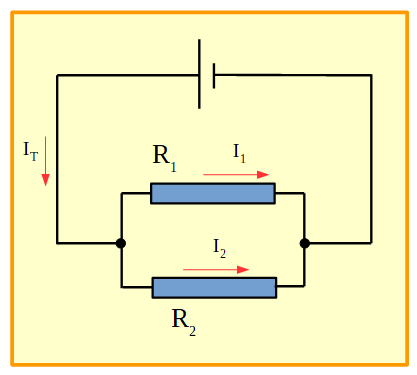
Figura 17. Circuito en paralelo.

Podemos ver que son posibles tres recorridos cerrados, es decir, este circuito posee tres mallas. Para cada una de las mallas aplicaremos lo visto antes:

$\Delta Vp - \Delta Vresistores = 0$

Malla 1

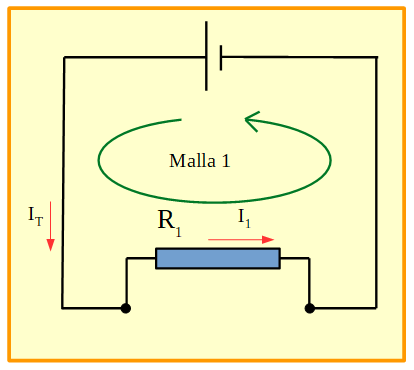
Figura 18. Circuito en el que se muestra la malla 1.

Si aplicamos la ley de las mallas para la malla 1, queda:

$\Delta Vp - \Delta V1 = 0$

es decir que:

$\Delta Vp = \Delta V1$

tal como vimos anteriormente para un circuito en paralelo.

Malla 2

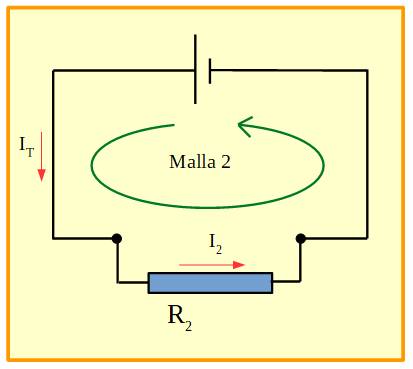
Figura 19. Circuito en el que se muestra la malla 2.

Si aplicamos la ley de las mallas para la malla 1, queda:

$\Delta Vp - \Delta V2 = 0$

es decir que:

$\Delta Vp = \Delta V2$

tal como vimos anteriormente para un circuito en paralelo.

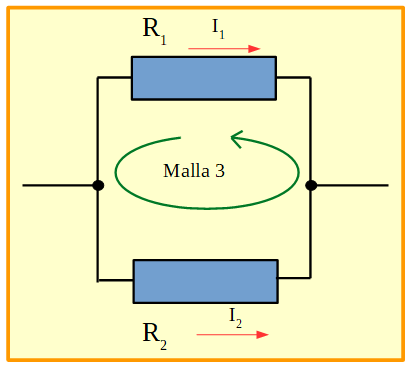
Figura 20. Circuito en el que se muestra la malla 3.

En esta última malla tenemos que hacer la siguiente aclaración: Si recorremos alguna parte del circuito en sentido opuesto al de la corriente convencional, el signo de la diferencia de potencial en los extremos del elemento que se encuentre en dicha zona, será opuesto al que le asignamos si recorremos en el sentido de la corriente convencional. En el caso de este ejemplo queda:

$\Delta V2 - \Delta V1 = 0$,

por lo tanto:

$\Delta V2 = \Delta V1$,

tal como vimos anteriormente. La diferencia de potencial de elementos conectados en paralelo, es la misma.