Física - 3º C.B.

Si sobre un sistema (cuerpo de la figura) actúan varias fuerzas:

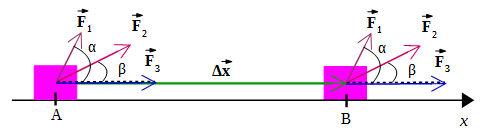
se puede determinar el trabajo total o neto de dos formas:

1) Determinando la fuerza neta y luego calculando el trabajo de la fuerza neta:

Siendo F_neta el módulo del vector fuerza neta, Δx , el módulo del vector desplazamiento y δ el ángulo entre el vector fuerza neta y el vector desplazamiento.

2) Calculando el trabajo de cada una de las fuerzas y luego sumando los trabajos de cada una:

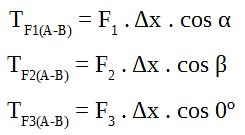
Ejemplo:

Sobre la valija de la figura actúan las fuerzas que están representadas, los valores de dichas fuerzas son:

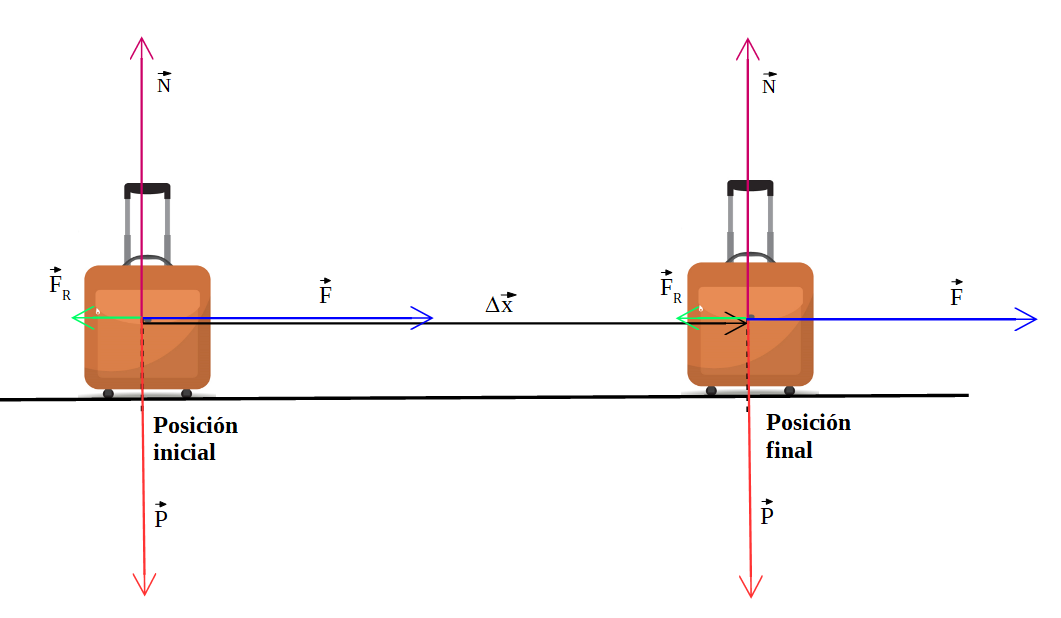
Los valores de las fuerzas son: F = 400 N,  Fr = 100 N, P = 400 N, el valor de la normal en este caso es igual al del peso, N = 400 N.

Determinar el trabajo neto realizado sobre la valija, si la misma se desplaza 100 m.

Solución:

Se puede determinar el trabajo de las dos formas descriptas más arriba. En este ejemplo los trabajos realizados por las fuerzas que actúan sobre la valija son calculados siempre entre la posición inicial y la final:

1) Se determina la fuerza neta, para ello se suman las fuerzas las fuerzas en la horizontal, en el eje x

Al ser colineales y tener sentido opuesto, el módulo de la fuerza resultante en el eje x se determina:

A continuación se suman las fuerzas en el eje vertical y:

la normal y el peso son colineales y de sentido opuesto por tanto:

La fuerza neta es la suma de las fuerzas en el eje x y en el eje y, como la suma de fuerzas en el eje y es cero, la resultante es solamente la suma de fuerzas hallada para el eje x:

su dirección es horizontal a la derecha:

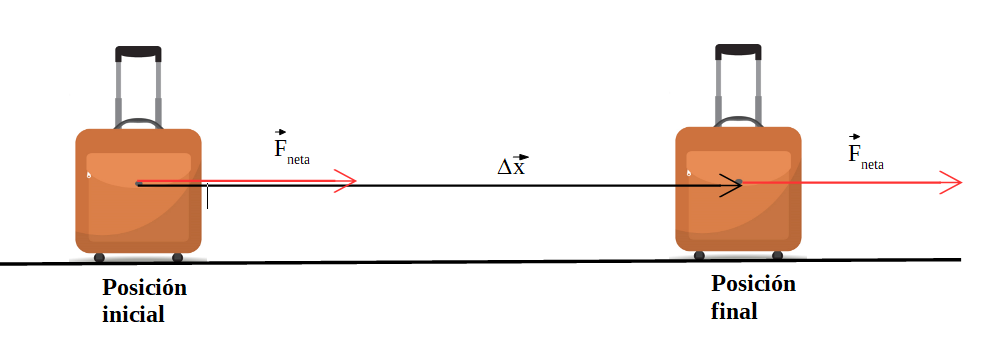
A continuación se determina el trabajo de la fuerza neta entre la posición inicial y final:

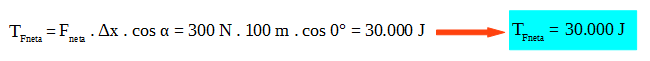
2) En la segunda forma de calcular el trabajo neto, se determina el trabajo de cada una de las fuerzas entre las posiciones inicial y final, y luego se suman:

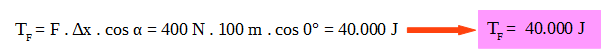
El ángulo α entre la fuerza y el desplazamiento es 0º.

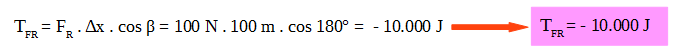
El ángulo  entre la fuerza de rozamiento y el desplazamiento es 180º.

El ángulo δ entre la fuerza normal y el desplazamiento es 90º.

El ángulo θ entre la fuerza peso y el desplazamiento es 90º.

El trabajo neto es entonces la suma de los trabajos de cada una de las fuerzas que actúan sobre la valija (entre las posiciones inicial y final):

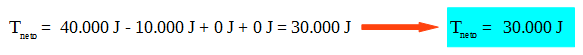
Se puede observar que el trabajo calculado por las dos formas da lo mismo.