Física - 3º C.B.
Trabajo mecánico
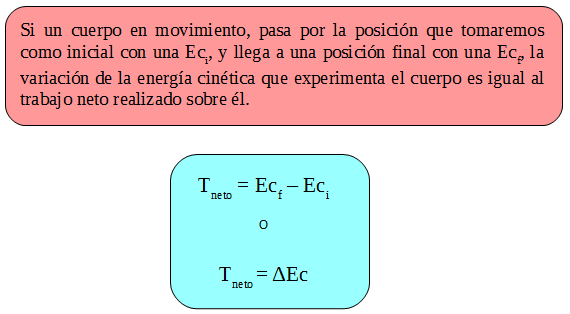
3. Relación entre el trabajo y la energía cinética
Sobre una caja que se encuentra en la posición inicial y se mueve con una velocidad inicial (cuyo valor es vi), se aplica una fuerza (Fneta porque es la resultante de todas las fuerzas aplicadas sobre la caja), como muestra la figura, como consecuencia la velocidad de la caja aumenta porque ésta se acelera.
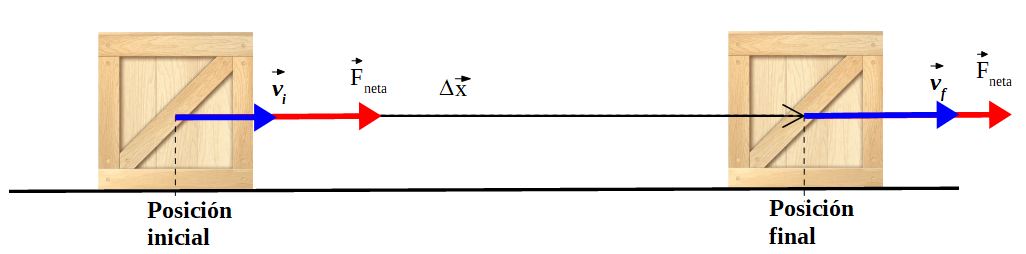
Esta fuerza realiza trabajo sobre la caja, le transfiere energía, la caja que inicialmente se encontraba moviéndose con una velocidad, es decir posee una Eci, aumenta su energía cinética, pues aumenta su velocidad, Ecf. Toda la energía transferida por el trabajo realizado por la fuerza se transforma en energía cinética, por tanto:
TFneta = ΔEc = Ecf - Eci
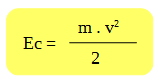
Resumiendo: