Física - 3º C.B.

La energía potencial está asociada a la posición relativa de las partículas en función de las interacciones fundamentales. Se analizan aquí los casos cuando la fuerza peso o la fuerza elástica realizan trabajo sobre un cuerpo y su relación con la energía potencial vinculada a esta transferencia.

* Relación entre el trabajo del peso y la energía potencial gravitatoria

La pelota de la figura se desplaza de la posición inicial a la final por la acción de la fuerza peso representada:

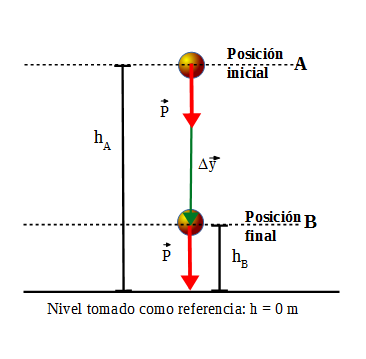
El trabajo realizado por la fuerza peso: puede ser que actúen otras fuerzas sobre la pelota, pero aquí sólo se focalizará en el trabajo que realiza la fuerza el peso. Por lo que el trabajo realizado por la fuerza peso desde A a B es:

T_P(A-B) = P . Δy . cos 0º

El módulo del desplazamiento de la pelota es Δy = h_A - h_B, y el módulo del peso P = m . g y cos 0º = 1

T_P(A-B) = m . g .  (h_A - h_B)

Por otro lado si analizamos las Epg inicial y final, vemos que inicialmente la pelota tiene una Epg_A = m . g . h_A. En la posición final su Epg_B = m . g . h_B. Por lo que su variación de Epg es: 

ΔEpg = Epg_B - Epg_A

ΔEpg = m . g . h_B  -  m . g . h_A

ΔEpg = m . g . (h_B  - h_A)

Al comparar:  T_P(A-B) = m . g .  (h_A - h_B) con ΔEpg = m . g . (h_B  - h_A) se observa que si a ΔEpg multiplicamos por -1 obtenemos T_P(A-B).

ΔEpg = m . g . (h_B  - h_A)        - ΔEpg = - m . g . (h_B  - h_A)        - ΔEpg = m . g . (h_A - h_B)       esta última expresión es igual a T_P(A-B) = m . g .  (h_A - h_B)

En conclusión:

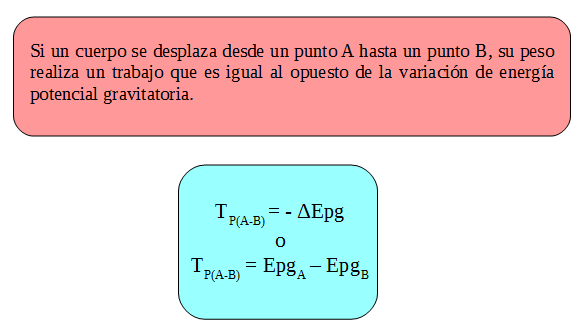
* Relación entre el trabajo de la fuerza elástica y la energía potencial elástica

De forma análoga a cómo se estudió la relación entre el trabajo del peso y la energía potencial gravitatoria se puede deducir que la relación entre el trabajo realizado por la fuerza elástica y la energía potencial elástica es:

* El trabajo también se relaciona con otras energías potenciales que no estudiaremos en este módulo.