Astronomía - 1º B.D.

La única estrella del Sistema Solar es el Sol, cuya distancia a la Tierra equivale a 1 Unidad Astronómica (150.000.000 kilómetros). Dentro del Sistema Solar es lógico expresar las distancias en kilómetros o Unidades Astronómicas (U.A.). Sin embargo el resto de las estrellas se encuentran a distancias tan grandes, que resulta poco práctico expresar su distancia en estas unidades. Por lo tanto debemos utilizar el año luz (a.l.) como unidad de distancia para los astros tan lejanos como las estrellas.

Sabemos que la estrella más cercana a la Tierra sin ser el Sol, es α Centauri, la cual se encuentra a 4,3 años luz. Mientras que a la luz del Sol le lleva 8 minutos aproximadamente recorrer la distancia Tierra - Sol, la luz de la estrella α Centauri demora 4,3 años en llegar la Tierra. Quiere decir que al observar en el cielo en la noche a α Centauri, la vemos como era 4,3 años atrás. Lo mismo ocurre con las demás estrellas que vemos en el cielo a simple vista, todas ellas se encuentran a diferentes distancias. Algunas están a decenas, otras a cientos o a miles de años luz de la Tierra. Por lo tanto podemos concluir que al mirar las estrellas en el cielo, estaremos viendo en realidad como eran estas estrellas en el pasado, tanto más antiguo según lejana sea la estrella.

PARALAJE ESTELAR: es el ángulo desde el cual un observador situado en la estrella puede ver el radio de la órbita terrestre. Se aprecia en la siguiente imagen (creada por los autores):

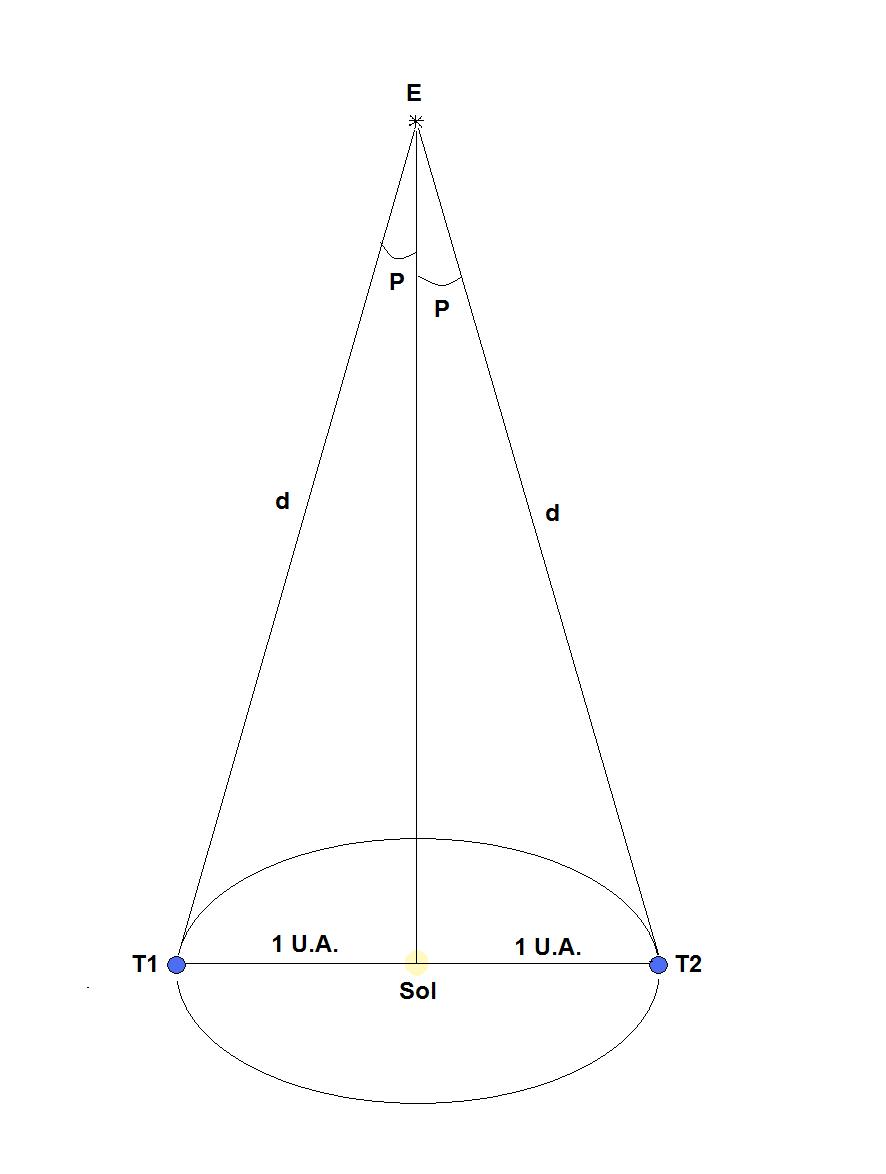
P: ángulo de paralaje - ángulo muy pequeño (para las estrellas es menor que un segundo de arco)

T1 y T2 son las posiciones de la Tierra en dos momentos separados por 6 meses de diferencia.

E es la estrella a la cual se quiere saber su distancia.

En el caso de α Centauri el ángulo de paralaje P= 0,76" (0 grados, 0 minutos, 0 segundos y 76 centésimas de segundo). Es el mayor valor de las paralajes por tratarse de la estrella más cercana.

Un punto ubicado a una distancia de 1 parsec de la Tierra, tendría un ángulo de paralaje P= 1".

Pero si nos alejamos hasta la distancia a la cual se encuentra la estrella Sirio (8,6 años luz), como representa el doble de la distancia de α Centauri, por lo tanto el ángulo de paralaje de Sirio se reduce a la mitad: P= 0,38".

El ángulo de paralaje actualmente se determina por medios fotográficos precisos. Si la Tierra se encuentra en la posición T1, en dicho instante se toma una foto de la estrella E, la que aparecerá en la posición E1. Al cabo de 6 meses, la Tierra se halla en la posición T2 y como consecuencia de ello la estrella se habrá aparentemente desviado a una posición E2, tal como lo ilustra la imagen (creada por los autores):

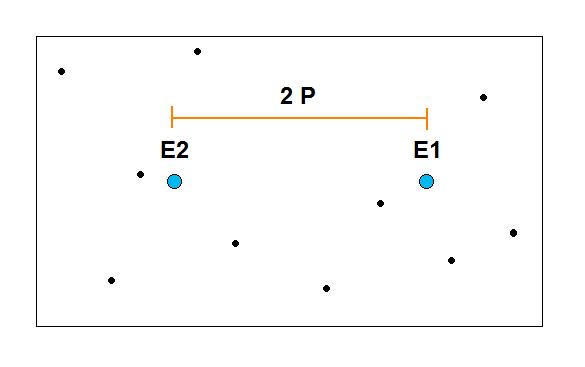
Mientras que las estrellas más lejanas permanecen en la misma posición al transcurrir los 6 meses, la estrella más cercana E experimenta el cambio de posición debido a la traslación de la Tierra alrededor del Sol. La distancia angular E2E1 se puede determinar en la placa fotográfica, ya que está cuidadosamente milimetrada. Esta distancia corresponde al ángulo 2P, es decir al doble del ángulo de paralaje, es decir que el ángulo de paralaje anual P tiene un valor igual a la mitad del desplazamiento angular observado.

En el triángulo Sol T1 Estrella tenemos valores conocidos: se sabe el valor del ángulo de paralaje P y se sabe que la distancia Tierra - Sol equivale a 1 U.A. Se aplica trigonometría:

sen P= 1 U.A. / d

Despejando: d= 1 / sen P

Como P es muy chico, se cumple: d= 1 / P

Se concluye que la distancia d a una estrella E, es inversamente proporcional a su paralaje.

Dicho valor d hallado se expresa en parsec (pc), unidad que ya fue definida. Mientras que el ángulo de paralaje P se expresa en segundos de arco (").