Química - 3º B.D.
¿Qué relación hay entre la concentración de los reactivos y la rapidez de una reacción?
2. ¿Cómo se puede determinar experimentalmente la ley de rapidez?
2.3. Ejemplo 3
![]()
Determina la ley de rapidez y el valor de k con los siguientes datos:
A + 2 B → AB2 | |||
Experimento | [A] (mol/L) | [B] (mol/L) | rinicial (mol/L.s) |
1 | 0,010 | 0,010 | 1,5.10-4 |
2 | 0,010 | 0,020 | 1,5.10-4 |
3 | 0,020 | 0,030 | 6,0.10-4 |

1. Comenzamos escribiendo la ley de la rapidez de forma general: r = k [A]x. [B]y

2. Selecciono los dos experimentos en donde la concentración del reactivo A no cambia, en este caso el experimento 1 y el 2.

3. Sustituyo los valores para cada caso:
- r1 = k [0,010 mol/L]x. [0,010 mol/L]y = 1,5.10-4 mol/L.s
- r2 = k [0,010 mol/L]x. [0,020 mol/L]y = 1,5.10-4 mol/L.s

4. Divido ambas expresiones, colocando como numerador la expresión en la que el reactivo B, en este caso el monóxido de nitrógeno, tiene una mayor concentración.
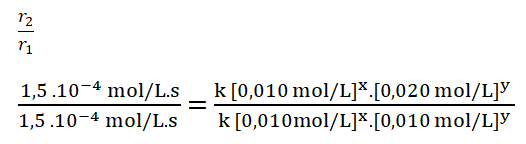

5. Simplifico aquellos términos iguales aplicando una cancelación:
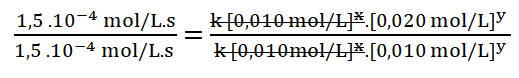
Divido los valores numéricos de la rapidez 2 sobre la 1.
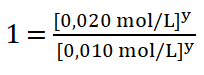
Divido entre sí los valores de la concentración del reactivo B aplicando la división de dos potencias de igual exponente.
![]()

6. Despejo el valor del orden parcial o potencia y aplicando la propiedad de las potencias (cualquier número distinto de cero elevado a la cero da uno) y obtengo que: ![]()

7. Repito los pasos anteriores seleccionando un experimento en donde la concentración del reactivo B se mantenga constante.
Selecciono los experimentos 2 y 3 en donde la concentración del reactivo B no cambia.
Sustituyo lo valores para cada experimento:
- r2 = k [0,010 mol/L]x. [0,020 mol/L]y = 1,5.10-4 mol/L.s
- r3 = k [0,020 mol/L]x. [0,030 mol/L]y = 6,0.10-4 mol/L.s
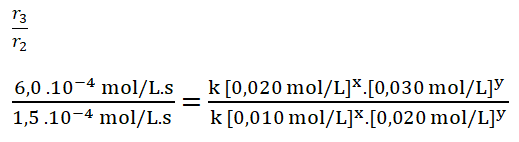
Simplifico los términos iguales tomando en cuenta también que el valor de y es cero, por lo que las concentraciones de B elevadas al exponente cero dan como resultado uno (a0 = 1, siendo a distinto de cero).
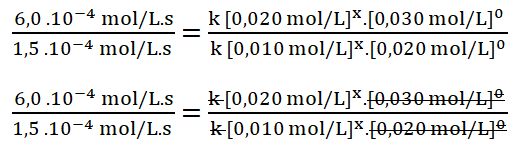
Divido los valores numéricos de la rapidez 3 sobre la 2.
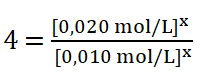
Divido entre sí los valores de la concentración del reactivo A.
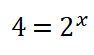

8. Despejo el valor del orden parcial o potencia x, obtengo que: 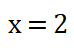

9. Selecciono uno de los experimentos, sustituyo los datos y despejo la k (constante específica).
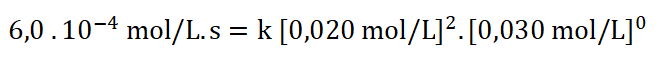
Despejo k:
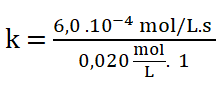
Simplificando las unidades:
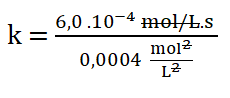
Finalmente:
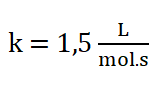

10. Escribo la ley de rapidez: r = 1,5 L/mol.s [A]2. [B]0 o r = 1,5 L/mol.s [A]2
Orden global = 2+0 = 2
